1. Toy模板网首页
  2. > Toy博客

蛮力算法之深度优先遍历和广度优先遍历——图的深度优先遍历和广度优先遍历，附带案例：迷宫问题及矩阵中传染性传播问题

10月前 作者：美人鱼战士与企鹅男孩合为一体 分类：Toy博客 阅读(65) 违法举报

这篇具有很好参考价值的文章主要介绍了蛮力算法之深度优先遍历和广度优先遍历——图的深度优先遍历和广度优先遍历，附带案例：迷宫问题及矩阵中传染性传播问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

算法：图的深度优先搜索和广度优先搜索

这两种搜索方法本质上都是基于蛮力法思路

这两种搜索方法对有向图和无向图都适用

1 图的两种定义方式

1.1 邻接矩阵

constexpr auto MAXV = 1000; //定义最大顶点个数

//顶点信息
typedef struct
{
	int no;
	char data[MAXV];
}VertexType;

//矩阵信息
typedef struct
{
	int edges[MAXV][MAXV];
	int n, e;
	VertexType vexs[MAXV];
}MGraph;

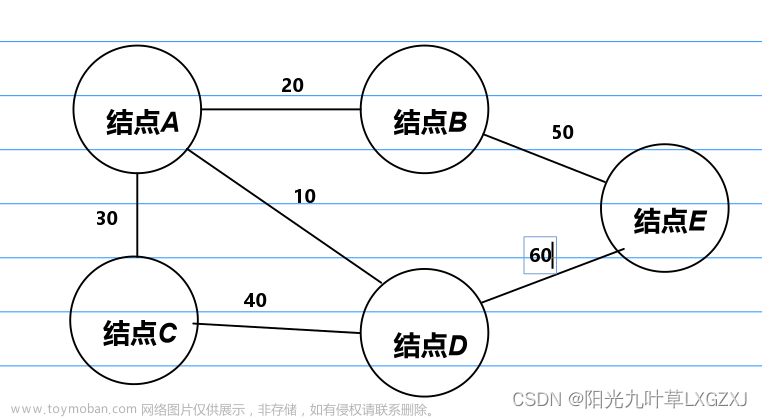
邻接矩阵示意图：

蛮力算法之深度优先遍历和广度优先遍历——图的深度优先遍历和广度优先遍历，附带案例：迷宫问题及矩阵中传染性传播问题,深度优先,算法,广度优先,c++,visualstudio,数据结构,图搜索

1.2 邻接表

注意：边结点代表的是图中的边，而并非图中的结点；头结点才表示图中的结点；头结点身后所连接的为边结点

//边结点 
typedef struct ANode
{
	int adjvex;			//这条边的终点
	int weight;			//这条边的权重
	struct ANode* nextarc;  //指向下一条与该结点相邻的边
} ArcNode;


//头结点
typedef struct VNode
{
	string date;		//顶点的其他信息
	ArcNode* firstarc;	//指向第一条边
};


//邻接表
typedef struct
{
	VNode adjList[MAXV];  //头结点组成的数组
	int n, e;            //图中的顶点数n和边数e
}ALGraph;

邻接表示意图：（一般默认为出边表）

蛮力算法之深度优先遍历和广度优先遍历——图的深度优先遍历和广度优先遍历，附带案例：迷宫问题及矩阵中传染性传播问题,深度优先,算法,广度优先,c++,visualstudio,数据结构,图搜索

2 图的深度优先遍历

关键：

  1. 用**visited[]**数组记录是否已访问
  2. 这是一个递归的过程

邻接矩阵的：

void DFS(MGraph g,int v)
{	int w;
	cout<<v<<" ";						//输出被访问顶点的编号
	visited[v]=1;						//置已访问标记
	for (w=0;w<g.n;w++)					//找顶点v的所有相邻点
		if (g.edges[v][w]!=0 && g.edges[v][w]!=INF && visited[w]==0)
			DFS(g,w);					//找顶点v的未访问过的相邻点w
}

邻接表的：

void DFS(ALGraph *G,int v)
{	ArcNode *p;
	cout<<v<<" ";					//输出被访问顶点的编号
	visited[v]=1;						//置已访问标记
	p=G->adjlist[v].firstarc;			//p指向顶点v的第一个邻接点
	while (p!=NULL)
	{	if (visited[p->adjvex]==0)		//若p->adjvex顶点未访问,递归访问它
			DFS(G,p->adjvex);
		p=p->nextarc;					//p指向顶点v的下一个邻接点
	}
}

3 图的广度优先遍历

关键：

  1. 使用数据结构 → 队列来记录未访问的邻接点
  2. 用**visited[]**数组记录哪些点已经访问了，哪些还没有
  3. 采用循环，循环终止条件为队列空了

邻接矩阵的：

void BFS(MGraph g,int v)					//邻接矩阵的DFS算法
{
	queue<int> qu;							//定义一个队列qu
	int visited[MAXV];						//定义存放结点的访问标志的数组
	int w,i;
	memset(visited,0,sizeof(visited));		//访问标志数组初始化

	cout<<v<<" ";						//输出被访问顶点的编号
	visited[v]=1;							//置已访问标记
	qu.push(v);								//v进队
	while (!qu.empty())						//队列不空时循环
	{
		w=qu.front(); qu.pop();				//出队顶点w
		for (i=0;i<g.n;i++)					//找与顶点w相邻的顶点
			if (g.edges[w][i]!=0 && g.edges[w][i]!=INF && visited[i]==0)
			{	//若当前邻接顶点i未被访问
				cout<<i<<" ";			//访问相邻顶点
				visited[i]=1;				//置该顶点已被访问的标志
				qu.push(i);					//该顶点进队
			}
	}
	printf("\n");
}

邻接表的：

void BFS(ALGraph *G,int v)					//邻接表的DFS算法
{
	ArcNode *p;
	queue<int> qu;							//定义一个队列qu
	int visited[MAXV];						//定义存放顶点的访问标志的数组
	int w;
	memset(visited,0,sizeof(visited));		//访问标志数组初始化
	cout<<v<<" ";						//输出被访问顶点的编号
	visited[v]=1; 							//置已访问标记
	qu.push(v);								//v进队
	while (!qu.empty())						//队列不空时循环
	{
		w=qu.front(); qu.pop();				//出队顶点w
		p=G->adjlist[w].firstarc;			//找顶点w的第一个邻接点
		while (p!=NULL) 
		{	if (visited[p->adjvex]==0)		//若当前邻接顶点未被访问
			{	cout<<i<<" ";	//访问相邻顶点
				visited[p->adjvex]=1;		//置该顶点已被访问的标志
				qu.push(p->adjvex);			//该顶点进队
			}
			p=p->nextarc;					//找顶点w的下一个邻接点
		}
	}
	printf("\n");
}

两种遍历方式都重点掌握邻接表的。

案例

案例1：迷宫

【问题描述】有如下8*8的迷宫图：

OXXXXXXX
OOOOOXXX
XOXXOOOX
XOXXOXXO
XOXXXXXX
XOXXOOOX
XOOOOXOO
XXXXXXXO

其中，O表示通路方块，X表示障碍方块。假设入口是位置（0，0），出口为右下角方块位置（7，7）。设计一个程序采用递归方法求指定入口到出口的一条迷宫路径。

深度优先的解法：

关键：

  1. 用数组记录垂直与水平偏移量，才能运用for循环遍历来尝试各种可能
  2. 采用递归，递归的终止条件为达到了终点
  3. 如何记录过程（路径）？在深度遍历的过程中，将可行的点作上了记号，不可行的点保留了原貌；最后输出矩阵即可
#include <stdio.h>
#define MAxN 10						//最大迷宫大小
//问题表示
int n=8;							//迷宫大小
char Maze[MAxN][MAxN]=
{	{'O','X','X','X','X','X','X','X'},
	{'O','O','O','O','O','X','X','X'},
	{'X','O','X','X','O','O','O','X'},
	{'X','O','X','X','O','X','X','O'},
	{'X','O','X','X','X','X','X','X'},
	{'X','O','X','X','O','O','O','X'},
	{'X','O','O','O','O','X','O','O'},
	{'X','X','X','X','X','X','X','O'}
};
int H[4] = {0, 1, 0, -1};			//水平偏移量,下标对应方位号0～3
int V[4] = {-1, 0, 1, 0};			//垂直偏移量

void disppath()						//输出一条迷宫路径
{
	for (int i=0; i<n;i++)
	{
		printf("    ");
		for(int j=0; j<n;j++)
			printf("%c",Maze[i][j]);
		printf("\n");
	}
}
void DFS(int x,int y)			 //求从(x,y)出发的一条迷宫路径
{
	if (x==n-1 && y==n-1) //找到一条路径,输出
	{
		Maze[n-1][n-1]=' ';
		disppath();
		return;
	}
	else
	{	for (int k=0;k<4;k++)				 //试探每一个方位
			if(x>=0 && y>=0 && x<n && y<n && Maze[x][y]=='O')
			{								//若(x,y)方块的可走的
				Maze[x][y]=' ';				//将该方块设置为空字符
				DFS(x+V[k],y+H[k]);			//查找(x,y)周围的每一个相邻方块
				Maze[x][y]='O';				//若从该相邻方块出发没有找到路径,恢复(x,y)
			}
	}
}
void main()
{
	int x=0,y=0;		//指定入口,出口默认为(n-1,n-1)
	printf("一条迷宫路径:\n");
	DFS(x,y);			//求(0,0)->(7,7)的一条迷宫路径
}

广度优先的解法：

关键：

  1. 用数组记录垂直与水平偏移量，才能运用for循环遍历来尝试各种可能
  2. 如何记录路径：采用队列，对于可行的方块，我们将其放入队列尾部（方块是用结构体定义的）
  3. 不会记录到多条路径吗？是的，队列中除了结果路径的点之外，还有广度遍历过程中其他路径上的点，所以，我们要用结构体来定义点，并赋予一个属性pre，用来记录这个点的前驱在队列中的下标（用数组加上队头队尾组成的队列支持随机访问）
  4. 在将方块添加到队列之前，要将其修改为某个特定的值防止其被再次访问到。例如A之后的B可行，接下来我们要以B为对象，判断它周围的方块是否可行，A也是其周围方块之一，但是不用再访问A了，因为之前已经访问过了
#include <stdio.h>
#define MAXQ 100					//队列大小
#define MAxN 10						//最大迷宫大小
//问题表示
int n=8;							//迷宫大小
char Maze[MAxN][MAxN]=
{	{'O','X','X','X','X','X','X','X'},
	{'O','O','O','O','O','X','X','X'},
	{'X','O','X','X','O','O','O','X'},
	{'X','O','X','X','O','X','X','O'},
	{'X','O','X','X','X','X','X','X'},
	{'X','O','X','X','O','O','O','X'},
	{'X','O','O','O','O','X','O','O'},
	{'X','X','X','X','X','X','X','O'}
};
int H[4] = {0, 1, 0, -1};			//水平偏移量,下标对应方位号0～3
int V[4] = {-1, 0, 1, 0};			//垂直偏移量
struct Position						//队列元素类型
{
	int x,y;						//当前方块位置
	int pre;						//前驱方块的下标
};
Position qu[MAXQ];					//定义一个队列qu
int front=-1,rear=-1;				//定义队头和队尾

void disppath(int front)			//输出一条迷宫路径
{
	int i,j;
	for (i=0; i<n;i++)				//将所有'*'改为'O'
		for (j=0;j<n;j++)
			if (Maze[i][j]=='*')
				Maze[i][j]='O';
	int k=front;
	while (k!=-1)					//即路径上的方块改为' '
	{
		Maze[qu[k].x][qu[k].y]=' ';
		k=qu[k].pre;
	}
	for (i=0; i<n;i++)				//输出迷宫路径
	{	printf("    ");
		for(int j=0; j<n;j++)
			printf("%c",Maze[i][j]);
		printf("\n");
	}
}

void BFS(int x,int y)			 //求从(x,y)出发的一条迷宫路径
{
	Position p,p1,p2;
	p.x=x; p.y=y; p.pre=-1;			//建立入口结点
	Maze[p.x][p.y]='*';				//改为'*'避免重复查找
	rear++; qu[rear]=p;				//入口方块进队
	while (front!=rear)				//队不空循环
	{
		front++; p1=qu[front];		//出队方块p1;
		if (p1.x==n-1 && p1.y==n-1)	//找到出口
		{
			disppath(front);		//输出路径
			return;
		}
		for (int k=0;k<4;k++)		//试探p1的每个相邻方位
		{
			p2.x=p1.x+V[k];			//找到p1的相邻方块p2
			p2.y=p1.y+H[k];
			if (p2.x>=0 && p2.y>=0 && p2.x<n && p2.y<n && Maze[p2.x][p2.y]=='O')
			{	//方块p2有效并且可走
				Maze[p2.x][p2.y]='*';	//改为'*'避免重复查找
				p2.pre=front;
				rear++;	qu[rear]=p2;	//方块p2进队
			}
		}
	}
}
void main()
{
	int x=0,y=0;		//指定入口,出口默认为(n-1,n-1)
	printf("一条迷宫路径:\n");
	BFS(x,y);			//求(0,0)->(7,7)的一条迷宫路径
}

案例2：传染

这个案例可以更好的理解广度优先遍历

小蓝有一个01矩阵。他打算将第一行第一列的 0 变为 2 。变化过程有传染性，每次 2 的上下左右四个相邻的位置中的 0 都会变成 2 。直到最后每个 2 的周围都是 1 或 2 结束。
请问，最终矩阵中有多少个 2 ？
以下是小蓝的矩阵，共 30 行 40 列。

0000100010000001101010101001001100000011
0101111001111101110111100000101010011111
1000010000011101010110000000001011010100
0110101010110000000101100100000101001001
0000011010100000111111001101100010101001
0110000110000000110100000000010010100011
0100110010000110000000100010000101110000
0010011010100110001111001101100110100010
1111000111101000001110010001001011101101
0011110100011000000001101001101110100001
0000000101011000010011111001010011011100
0000100000011001000100101000111011101100
0010110000001000001010100011000010100011
0110110000100011011010011010001101011011
0000100100000001010000101100000000000010
0011001000001000000010011001100101000110
1110101000011000000100011001001100111010
0000100100111000001101001000001010010001
0100010010000110100001100000110111110101
1000001001100010011001111101011001110001
0000000010100101000000111100110010101101
0010110101001100000100000010000010110011
0000011101001001000111011000100111010100
0010001100100000011000101011000000010101
1001111010010110011010101110000000101110
0110011101000010100001000101001001100010
1101000000010010011001000100110010000101
1001100010100010000100000101111111111100
1001011010101100001000000011000110110000
0011000100011000010111101000101110110001

思路：广度优先遍历，当队列为空时为循环终止条件，计算矩阵中2的个数

#include<iostream>
#define MAXQ 100					
#define MAxN 100						
using namespace std;

int Maze[MAxN][MAxN] =
{ 
  {0,0,0,0,1,0,0,0,1,0,0,0,0,0,0,1,1,0,1,0,1,0,1,0,1,0,0,1,0,0,1,1,0,0,0,0,0,0,1,1},
  {0,1,0,1,1,1,1,0,0,1,1,1,1,1,0,1,1,1,0,1,1,1,1,0,0,0,0,0,1,0,1,0,1,0,0,1,1,1,1,1},
  {0,1,0,1,1,1,1,0,0,1,1,1,1,1,0,1,1,1,0,1,1,1,1,0,0,0,0,0,1,0,1,0,1,0,0,1,1,1,1,1},
  {1,0,0,0,0,1,0,0,0,0,0,1,1,1,0,1,0,1,0,1,1,0,0,0,0,0,0,0,0,0,1,0,1,1,0,1,0,1,0,0},
  {0,1,1,0,1,0,1,0,1,0,1,1,0,0,0,0,0,0,0,1,0,1,1,0,0,1,0,0,0,0,0,1,0,1,0,0,1,0,0,1},
  {0,0,0,0,0,1,1,0,1,0,1,0,0,0,0,0,1,1,1,1,1,1,0,0,1,1,0,1,1,0,0,0,1,0,1,0,1,0,0,1},
  {0,1,1,0,0,0,0,1,1,0,0,0,0,0,0,0,1,1,0,1,0,0,0,0,0,0,0,0,0,1,0,0,1,0,1,0,0,0,1,1},
  {0,1,0,0,1,1,0,0,1,0,0,0,0,1,1,0,0,0,0,0,0,0,1,0,0,0,1,0,0,0,0,1,0,1,1,1,0,0,0,0},
  {0,0,1,0,0,1,1,0,1,0,1,0,0,1,1,0,0,0,1,1,1,1,0,0,1,1,0,1,1,0,0,1,1,0,1,0,0,0,1,0},
  {1,1,1,1,0,0,0,1,1,1,1,0,1,0,0,0,0,0,1,1,1,0,0,1,0,0,0,1,0,0,1,0,1,1,1,0,1,1,0,1},
  {0,0,1,1,1,1,0,1,0,0,0,1,1,0,0,0,0,0,0,0,0,1,1,0,1,0,0,1,1,0,1,1,1,0,1,0,0,0,0,1},
  {0,0,0,0,0,0,0,1,0,1,0,1,1,0,0,0,0,1,0,0,1,1,1,1,1,0,0,1,0,1,0,0,1,1,0,1,1,1,0,0},
  {0,0,0,0,1,0,0,0,0,0,0,1,1,0,0,1,0,0,0,1,0,0,1,0,1,0,0,0,1,1,1,0,1,1,1,0,1,1,0,0},
  {0,0,1,0,1,1,0,0,0,0,0,0,1,0,0,0,0,0,1,0,1,0,1,0,0,0,1,1,0,0,0,0,1,0,1,0,0,0,1,1},
  {0,1,1,0,1,1,0,0,0,0,1,0,0,0,1,1,0,1,1,0,1,0,0,1,1,0,1,0,0,0,1,1,0,1,0,1,1,0,1,1},
  {0,0,0,0,1,0,0,1,0,0,0,0,0,0,0,1,0,1,0,0,0,0,1,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,1,0},
  {0,0,1,1,0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,1,1,0,0,1,1,0,0,1,0,1,0,0,0,1,1,0},
  {1,1,1,0,1,0,1,0,0,0,0,1,1,0,0,0,0,0,0,1,0,0,0,1,1,0,0,1,0,0,1,1,0,0,1,1,1,0,1,0},
  {0,0,0,0,1,0,0,1,0,0,1,1,1,0,0,0,0,0,1,1,0,1,0,0,1,0,0,0,0,0,1,0,1,0,0,1,0,0,0,1},
  {0,1,0,0,0,1,0,0,1,0,0,0,0,1,1,0,1,0,0,0,0,1,1,0,0,0,0,0,1,1,0,1,1,1,1,1,0,1,0,1},
  {1,0,0,0,0,0,1,0,0,1,1,0,0,0,1,0,0,1,1,0,0,1,1,1,1,1,0,1,0,1,1,0,0,1,1,1,0,0,0,1},
  {0,0,0,0,0,0,0,0,1,0,1,0,0,1,0,1,0,0,0,0,0,0,1,1,1,1,0,0,1,1,0,0,1,0,1,0,1,1,0,1},
  {0,0,1,0,1,1,0,1,0,1,0,0,1,1,0,0,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,1,0,1,1,0,0,1,1},
  {0,0,0,0,0,1,1,1,0,1,0,0,1,0,0,1,0,0,0,1,1,1,0,1,1,0,0,0,1,0,0,1,1,1,0,1,0,1,0,0},
  {0,0,1,0,0,0,1,1,0,0,1,0,0,0,0,0,0,1,1,0,0,0,1,0,1,0,1,1,0,0,0,0,0,0,0,1,0,1,0,1},
  {1,0,0,1,1,1,1,0,1,0,0,1,0,1,1,0,0,1,1,0,1,0,1,0,1,1,1,0,0,0,0,0,0,0,1,0,1,1,1,0},
  {0,1,1,0,0,1,1,1,0,1,0,0,0,0,1,0,1,0,0,0,0,1,0,0,0,1,0,1,0,0,1,0,0,1,1,0,0,0,1,0},
  {1,1,0,1,0,0,0,0,0,0,0,1,0,0,1,0,0,1,1,0,0,1,0,0,0,1,0,0,1,1,0,0,1,0,0,0,0,1,0,1},
  {1,0,0,1,1,0,0,0,1,0,1,0,0,0,1,0,0,0,0,1,0,0,0,0,0,1,0,1,1,1,1,1,1,1,1,1,1,1,0,0},
  {1,0,0,1,0,1,1,0,1,0,1,0,1,1,0,0,0,0,1,0,0,0,0,0,0,0,1,1,0,0,0,1,1,0,1,1,0,0,0,0},
  {0,0,1,1,0,0,0,1,0,0,0,1,1,0,0,0,0,1,0,1,1,1,1,0,1,0,0,0,1,0,1,1,1,0,1,1,0,0,0,1}
};


int H[4] = { 0, 1, 0, -1 };			//水平偏移量,下标对应方位号0～3
int V[4] = { -1, 0, 1, 0 };			//垂直偏移量

struct Position						//队列元素类型
{
	int x, y;						//当前方块位置
};

Position qu[MAXQ];					//定义一个队列qu
int front = -1, rear = -1;			//定义队头和队尾


//输出迷宫并输出迷宫中的2的个数
void print_2()
{
	int count = 0;
	for (int i = 0; i < 30; i++)
	{
		for (int j = 0; j < 40; j++)
		{
			cout << Maze[i][j];
			if (Maze[i][j] == 2)
			{
				count++;
			}
		}
		cout << endl;
	}
	cout << "迷宫中2的个数为：" << count << endl;
}


void BFS(int x, int y)			 //求从(x,y)出发的一条迷宫路径
{
	Position p, p1, p2;
	p.x = x; p.y = y; 		//建立入口结点
	Maze[p.x][p.y] = 2;				//改为2避免重复查找
	rear++; qu[rear] = p;				//入口方块进队
	while (front != rear)				//队不空循环
	{
		front++; p1 = qu[front];		//出队方块p1;
		for (int k = 0; k < 4; k++)		//试探p1的每个相邻方位
		{
			p2.x = p1.x + V[k];			//找到p1的相邻方块p2
			p2.y = p1.y + H[k];
			if (p2.x >= 0 && p2.y >= 0 && p2.x < 30 && p2.y < 40 && Maze[p2.x][p2.y] == 0)
			{	//方块p2有效并且可走
				Maze[p2.x][p2.y] = 2;	//改为2避免重复查找
				rear++;	qu[rear] = p2;	//方块p2进队
			}
		}
	}
	print_2();
}

int main()
{
	int x = 0, y = 0;		
	BFS(x, y);
	return 0;
}

输出结果：

蛮力算法之深度优先遍历和广度优先遍历——图的深度优先遍历和广度优先遍历，附带案例：迷宫问题及矩阵中传染性传播问题,深度优先,算法,广度优先,c++,visualstudio,数据结构,图搜索

案例3：跳动方格

如果两个相邻方格（上下左右四个方向相邻）内的数的最大公约数大于 1 ，则可以从其中一个方格移动到另一个方格，当然也可以从另一个方格移回第一个方格。
假设开始时站在第 r 行第 c 列，请问可以移动到方格图内的多少个方格？

样例输入

3 4
3 6 5 5
2 4 3 5
7 8 3 8
3 2

样例输出

5

思路：采用广度优先遍历，在将可行的方格放入到队列之前，计数+1

易错点+技巧点：

二维数组的初始化；

用同样尺寸的数组记录某个位置是否已经被访问过了；

没有记录路线的要求就可以不使用pre属性

二维数组的动态初始化：

//动态定义一个二维数组，并将其全部值初始化为0
	int** map;
	map = new int* [m];
	
	for (int i = 0; i < m; i++)
	{
        int* row = new int[n];
		for (int j = 0; j < n; j++)
		{
			row[j] = 1;
		}
		map[i] = row;
	}

或者

//动态定义一个二维数组，并将其全部值初始化为0
	int** map;
	map = new int* [m];

	for (int i = 0; i < m; i++)
	{
		map[i] = new int[n];
		for (int j = 0; j < n; j++)
		{
			map[i][j] = 1;
		}
	}

使用memset

int** map = new int* [m];
for (int i = 0; i < m; ++i) {
	map[i] = new int[n];
	memset(map[i], 3, n * sizeof(int));
}

#include<iostream>
#define MAXQ 100					//队列大小
#define MAxN 100						//最大迷宫大小
using namespace std;

int** map;
int** flag;	//记录是否已经被访问了
int m;
int n;

int H[4] = { 0, 1, 0, -1 };			//水平偏移量,下标对应方位号0～3
int V[4] = { -1, 0, 1, 0 };			//垂直偏移量

struct Position						//队列元素类型
{
	int x, y;//当前方块位置
};

Position qu[MAXQ];					//定义一个队列qu
int front = -1, rear = -1;			//定义队头和队尾

bool moreThanOne(int x, int y)
{
	//两个数的最大公约数大于1，返回true
	int theSmallOne = x < y ? x : y;
	for (int i = 2; i <= theSmallOne; i++)
	{
		if (x % i == 0 && y % i == 0) return true;
	}
	return false;
}

void printMap()
{
	for (int i = 0; i < m; i++)
	{
		for (int j = 0; j < n; j++)
		{
			cout << map[i][j]<<"  ";
		}
		cout << endl;
	}
}

void BFS(int x, int y)			 
{
	int count = 0;          //记录可以跳跃的个数
	Position p, p1, p2;
	p.x = x; p.y = y; 		//建立入口结点			
	rear++; qu[rear] = p;		
	count++;

	while (front != rear)				//队不空循环
	{
		front++; p1 = qu[front];		//出队方块p1;
		for (int k = 0; k < 4; k++)		//试探p1的每个相邻方位
		{
			p2.x = p1.x + V[k];			//找到p1的相邻方块p2
			p2.y = p1.y + H[k];

			if (p2.x >= 0 && p2.y >= 0 && p2.x < m && p2.y < n && moreThanOne(map[p2.x][p2.y], map[p1.x][p1.y]) && flag[p2.x][p2.y] != -1)
			{
				//方块p2有效并且可走
				flag[p1.x][p1.y] = -1;	//改为-1避免重复查找
				rear++;	qu[rear] = p2;	//方块p2进队
				count++;
			}
		}
	}

	printMap();
	cout << count << endl;
}

int main()
{
	//初始化矩阵
	cin >> m >> n;
	map = new int* [m];       //动态初始化二维数组这一步很重要，但是这一步最容易忘
	flag = new int* [m];
	for (int i = 0; i < m; i++)
	{
		int* row = new int[n];
		int* flag_row = new int[n];
		for (int j = 0; j < n; j++)
		{
			cin >> row[j];
			flag_row[j] = 0;
		}
		map[i] = row;
		flag[i] = flag_row;
	}

	//输入初始化的位置
	int x, y;
	cin >> x >> y;
	BFS(x - 1, y - 1);

	return 0;
}

运行结果：

蛮力算法之深度优先遍历和广度优先遍历——图的深度优先遍历和广度优先遍历，附带案例：迷宫问题及矩阵中传染性传播问题,深度优先,算法,广度优先,c++,visualstudio,数据结构,图搜索文章来源地址https://www.toymoban.com/news/detail-754785.html

到了这里，关于蛮力算法之深度优先遍历和广度优先遍历——图的深度优先遍历和广度优先遍历，附带案例：迷宫问题及矩阵中传染性传播问题的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • Python 算法基础篇之图的遍历算法：深度优先搜索和广度优先搜索

    2023年10月31日
    浏览(55)
  • 【数据结构与算法】图的基本概念 | 邻接矩阵和邻接表 | 广度优先遍历和深度优先遍历

    【数据结构与算法】图的基本概念 | 邻接矩阵和邻接表 | 广度优先遍历和深度优先遍历

    🌠 作者：@ 阿亮joy. 🎆 专栏：《数据结构与算法要啸着学》 🎇 座右铭：每个优秀的人都有一段沉默的时光，那段时光是付出了很多努力却得不到结果的日子，我们把它叫做扎根 图是由顶点集合及顶点间的关系组成的一种数据结构：G = (V， E) ，其中： 顶点集合V = {x|x属于某

    2024年02月04日
    浏览(73)
  • 数据结构与算法基础-学习-24-图的遍历之DFS（深度优先搜索）和BFS（广度优先搜索）

    数据结构与算法基础-学习-24-图的遍历之DFS（深度优先搜索）和BFS（广度优先搜索）

    目录 一、遍历定义 二、遍历实质 三、DFS 四、BFS 五、宏定义 六、自定义类型 七、函数实现 1、DFS（邻接矩阵实现） 2、DFS（邻接表实现） 3、BFS（邻接矩阵实现） 4、BFS（邻接表实现） 5、打印邻接矩阵遍历顺序  6、打印邻接表遍历顺序 八、遍历算法效率分析 1、DFS 2、BFS 九

    2024年02月03日
    浏览(74)
  • 图的遍历——深度优先遍历与广度优先遍历

    图的遍历——深度优先遍历与广度优先遍历

    目录 何谓遍历？ 图的遍历特点 图的遍历方式 深度优先搜索 过程分析 案例分析： 算法的代码实现  测试案例： 测试结果如下： 遍历非连通图 算法复杂度分析 额外补充 广度优先搜索 过程分析 辅助队列 算法的代码实现 队列部分 广度搜索部分 测试案例： 测试结果： 非连

    2024年02月04日
    浏览(41)
  • 图的广度优先遍历和深度优先遍历

    图的广度优先遍历和深度优先遍历

    前言：在上一篇博客我们学习了图的基本操作，包括图的建立、结点插入与删除等操作，怎么判断我们建立的图是否正确，很简单把它输出出来就是，但是如何输出它，这就是图的遍历问题了。 图的遍历是指从图中的某一顶点出发，按照某种搜索方法沿着图中的边对图中的所

    2024年02月11日
    浏览(50)
  • 图的两种遍历：深度优先遍历+广度优先遍历

    图的两种遍历：深度优先遍历+广度优先遍历

    深度优先遍历 是指按照 深度方向 搜索，它类似于树的先根遍历，是树的先根遍历的推广。 基本思想（通俗） 选一条路走到 底 ，直到 走不通 ，就 原路返回 看看 是否还有路 可走，如果返回到起点还无路可走，说明深度优先遍历已完成。 这是要深度遍历的 无向图 ：    深

    2024年02月06日
    浏览(46)
  • 图的二种遍历-广度优先遍历和深度优先遍历

    图的二种遍历-广度优先遍历和深度优先遍历

    1.树的广度优先遍历 这样一个图中，是如何实现广度优先遍历的呢，首先，从1遍历完成之后，在去遍历2,3,4，最后遍历5 ，6 , 7  , 8。这也就是为什么叫做广度优先遍历，是一层一层的往广的遍历 不存在“回路”，搜索相邻的结点时，不可能搜到已经访问过的结点 树的广度优

    2024年02月02日
    浏览(50)
  • 图的遍历（广度优先遍历BFS，深度优先遍历DFS）

    图的遍历（广度优先遍历BFS，深度优先遍历DFS）

    目录 图的遍历概念： 图的广度优先遍历（BFS）： 代码实现如下： 测试如下： 注意： 图的深度优先遍历（DFS）： 代码实现如下： 测试如下： 总代码： 结语： 给定一个图G和其中任意一个顶点v0，从v0出发，沿着图中各边访问图中的所有顶点，且每个顶点仅被遍历一次。\\\"遍

    2024年02月21日
    浏览(56)

  • 图的遍历-深度优先遍历与广度优先遍历（C语言）

    图的遍历 概念：指的是从图中的任一顶点出发，对图中的所有顶点访问一次且只访问一次。 邻接矩阵及邻接表的创建 ： 图的存储结构-无向邻接矩阵与无向邻接表（C语言）. 结构定义 邻接矩阵的深度优先遍历操作 邻接矩阵的深度优先递归算法 结构定义 邻接表的深度优先遍

    2024年02月06日
    浏览(48)
  • 大话数据结构-图的深度优先遍历和广度优先遍历

    大话数据结构-图的深度优先遍历和广度优先遍历

      图的遍历分为深度优先遍历和广度优先遍历两种。   深度优先遍历（Depth First Search），也称为深度优先搜索，简称DFS，深度优先遍历，是指从某一个顶点开始，按照一定的规则，访问并记录下一个未访问顶点。对于非连通图，则是按连通分量，采用同一规则进行深度优

    2024年02月04日
    浏览(58)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包