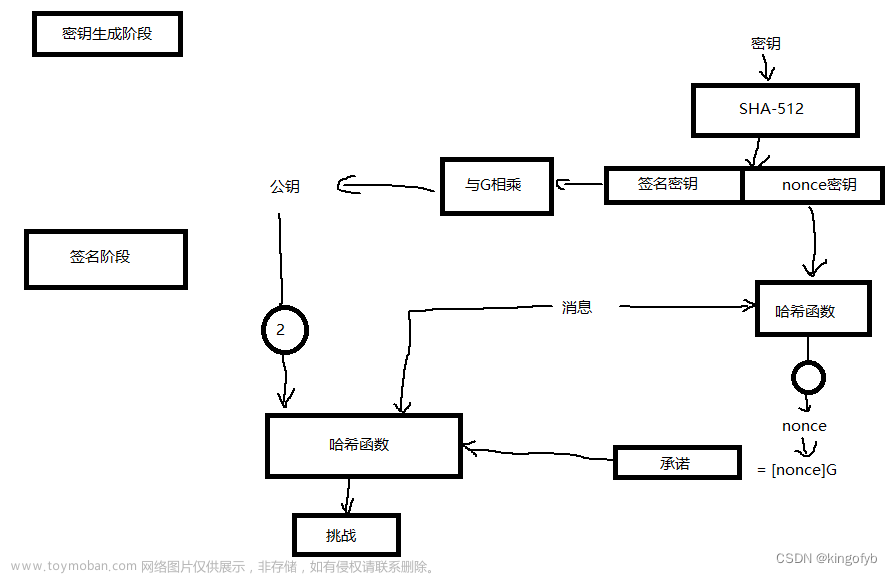
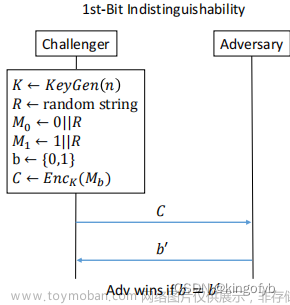
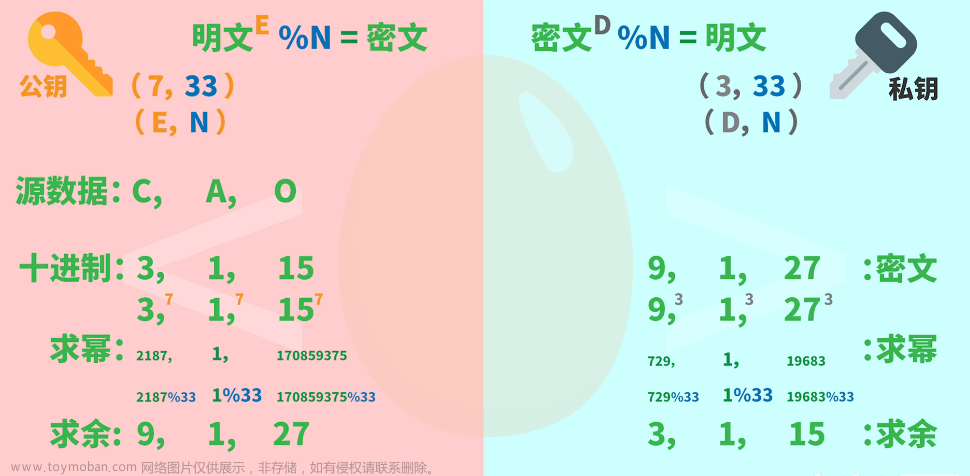
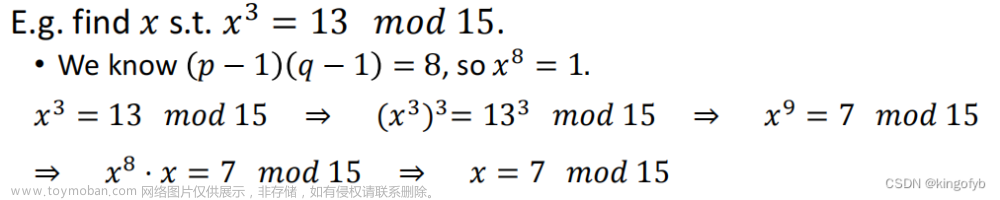密码学学习笔记(二十三)：哈希函数的安全性质：抗碰撞性，抗第一原象性和抗第二原象性-Toy模板网

这篇具有很好参考价值的文章主要介绍了密码学学习笔记(二十三)：哈希函数的安全性质：抗碰撞性，抗第一原象性和抗第二原象性。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

在密码学中，哈希函数是一种将任意长度的数据映射到固定长度输出的函数，这个输出通常称为哈希值。理想的哈希函数需要具备几个重要的安全性质，以确保数据的完整性和验证数据的来源。这些性质包括抗碰撞性、抗第一原象性和抗第二原象性。

抗碰撞性（Collision Resistance）

抗碰撞性指的是在合理的时间内很难找到两个不同的输入x和y使得它们的哈希值相同，即。对于所有，找到是不可行的。

假设有一个哈希函数 H，其输出是一个128位的哈希值。为了证明这个函数具有抗碰撞性，我们需要展示即使在大量尝试之后也很难找到两个不同的输入导致相同的哈希值。

在密码学中，这通常通过展示哈希函数能够抵抗“生日攻击”来完成。生日攻击是一种概率攻击，其原理类似于生日悖论：在一个23人的房间中，至少有两人生日相同的概率超过50%。

在哈希函数的上下文中，这意味着在次尝试后，找到一对碰撞的概率超过50%，其中 n 是哈希值的位数。因此，如果我们的哈希函数 H 在超过次尝试后仍然没有碰撞，我们可以认为它具有良好的抗碰撞性。在实际应用中，如密码存储或数字签名，开发者会选择已知具有强抗碰撞性的哈希函数。

抗第一原象性意味着对于给定的哈希值 h，在合理的时间内很难找到任何原始输入 x，使得。对于给定的h,找到任意x使得是计算不可行的。

这是一个理论上的属性。例如，如果攻击者获得了数据库中的哈希密码，他们不应该能够找到对应的密码。

假设一个黑客获得了一个哈希值 h，他们想要找到一个消息 m 使得。如果哈希函数是抗第一原象的，黑客尝试所有可能的输入直到他们找到一个匹配的原象，这个过程应该是不切实际的。例如，如果一个哈希函数的输出是256位长，黑客将需要尝试个不同的输入才能找到正确的原象，这在现实中是不可行的。

抗第二原象性指的是对于一个固定的输入 x，在合理的时间内很难找到一个不同的输入 y，使得。对于固定的x和任意的,找到H(x)=H(y)是计算不可行的。这保证了即使攻击者知道一个特定的输入和它的哈希值，他们也不能找到另一个具有相同哈希值的不同输入。

考虑一个电子文件签名的场景，Alice 用哈希函数 H 对文件 f 生成一个哈希值 h=H(f) 并用她的私钥加密它，创建一个数字签名。Bob 可以用Alice的公钥解密并得到 h，然后自己对文件 f 运行 H 来验证签名。

如果一个攻击者想要伪造一个签名，他们需要找到一个不同的文件 f′ 使得 H(f′)=h。如果哈希函数是抗第二原象的，那么找到这样的 f′ 将是非常困难的。

在这些例子中，一个关键的假设是哈希函数的输出空间足够大，这样概率才会站在我们这一边使得找到满足上述条件的输入变得不现实。在实践中，这就是为什么推荐使用比如SHA-256或更高位数哈希函数的原因，因为它们为找到原象或碰撞提供了足够小的概率。

MAC涉及的是一个哈希函数和一个密钥，用于验证消息的完整性和真实性。它结合了哈希函数的抗碰撞性和密钥的保密性，使得即使有人可以找到哈希函数的碰撞，他们也无法生成有效的MAC，因为他们不知道密钥。

其中 k 是密钥，m 是消息，H 是哈希函数，|| 表示连接。文章来源地址https://www.toymoban.com/news/detail-754843.html

到了这里，关于密码学学习笔记(二十三)：哈希函数的安全性质：抗碰撞性，抗第一原象性和抗第二原象性的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！