【数据结构】图的广度优先遍历-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】图的广度优先遍历。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.算法思想

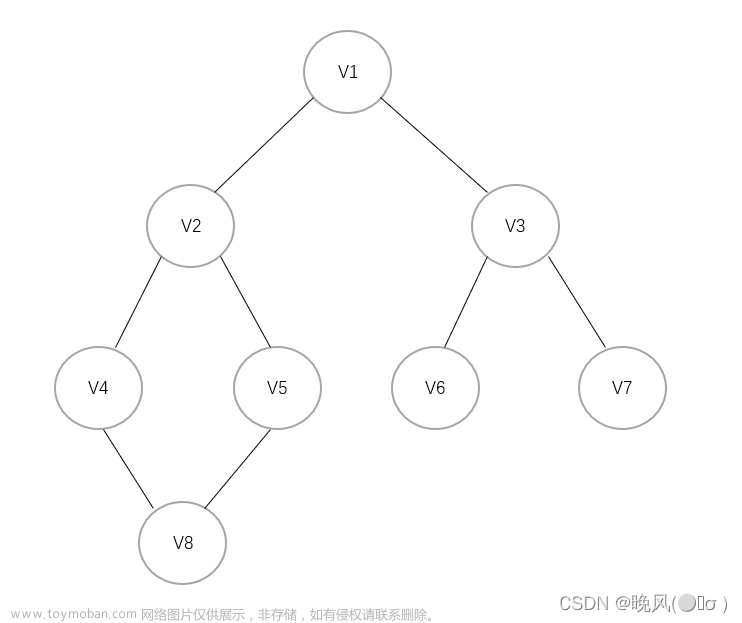
广度优先遍历，类似于树的层次遍历，又是熟悉的队列实现。首先将第一个顶点添加到队列中，然后讲该顶点的所有邻接顶点都加入队列中，再将该顶点输出。如此重复直到遍历完整个图。

2.定义结构体

typedef struct {
    char vertex[VERTEXNUM];
    int edge[VERTEXNUM][VERTEXNUM];
    int n,e;
} MGraph;

3.函数实现

Q:队列，用于存放顶点。
front,rear:队头和队尾指针，用于入队和出队。
p:工作指针，用于输出队头顶点。

首先将第一个顶点v入队，然后修改其访问标志为1。将其出队，输出该顶点。由工作指针p将该顶点的所有未访问的顶点添加到队列中。当某个顶点的访问标志位为0，且该顶点与当前顶点存在边时，说明改顶点是满足要求的，否则不满足要求。

void BFS(MGraph G, int v) {
    int Q[VERTEXNUM];//队列，存放顶点
    int front=-1,rear=-1,p=-1;
    Q[++rear] = v;
    visited[v] = 1;
    while(front < rear) {
        p = Q[++front];//出队
        printf("%c\t",G.vertex[p]);
        for(int i=0; i<G.n; i++) {//将满足条件的顶点都加入队列中
            if(!visited[i] && G.edge[p][i] !=0 && G.edge[p][i] != INFINITY) {
                Q[++rear] = i;
                visited[i] = 1;
            }
        }
    }
}

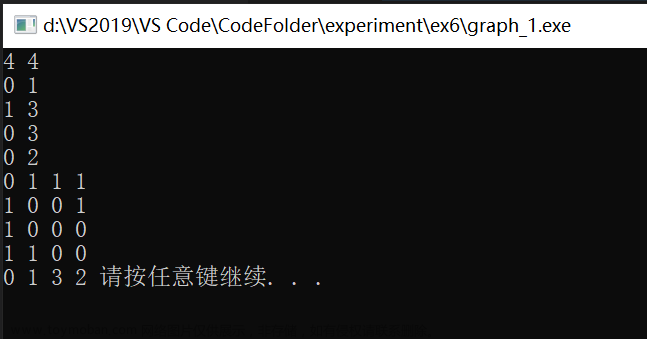
4.测试结果

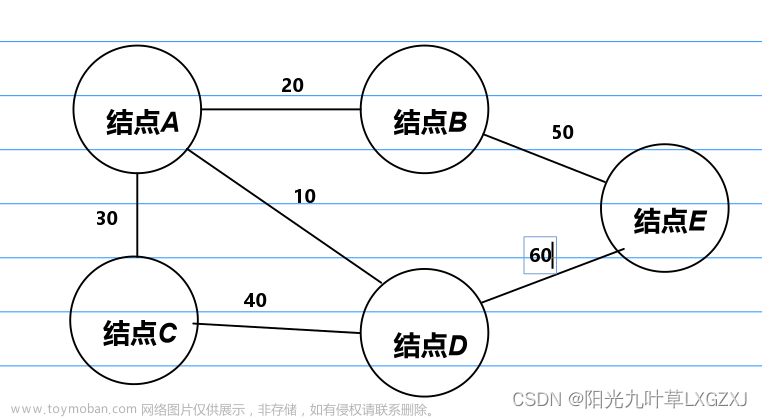
使用如下图进行测试：
图的广度优先遍历代码,数据结构,数据结构,算法,c语言,广度优先,图论

BFS(G,0);//从A开始遍历

图的广度优先遍历代码,数据结构,数据结构,算法,c语言,广度优先,图论

BFS(G,4);//从E开始遍历

图的广度优先遍历代码,数据结构,数据结构,算法,c语言,广度优先,图论 )文章来源地址https://www.toymoban.com/news/detail-754891.html

5.完整代码

#include <stdio.h>
#include <malloc.h>
#define INFINITY -1
#define VERTEXNUM 10

int visited[VERTEXNUM];

typedef struct {
    char vertex[VERTEXNUM];
    int edge[VERTEXNUM][VERTEXNUM];
    int n,e;
} MGraph;

void BFS(MGraph G, int v) {
    int Q[VERTEXNUM];//队列，存放顶点
    int front=-1,rear=-1,p=-1;
    Q[++rear] = v;
    visited[v] = 1;
    while(front < rear) {
        p = Q[++front];//出队
        printf("%c\t",G.vertex[p]);
        for(int i=0; i<G.n; i++) {//将满足条件的顶点都加入队列中
            if(!visited[i] && G.edge[p][i] !=0 && G.edge[p][i] != INFINITY) {
                Q[++rear] = i;
                visited[i] = 1;
            }
        }
    }
}


int main(int argc, char const *argv[]) {
    MGraph G; //初始化
    G.n = 5, G.e = 5;
    G.vertex[0] = 'A';
    G.vertex[1] = 'B';
    G.vertex[2] = 'C';
    G.vertex[3] = 'D';
    G.vertex[4] = 'E';
    G.edge[0][0] = 0;
    G.edge[0][1] = G.edge[1][0] = 5;
    G.edge[0][2] = G.edge[2][0] = 2;
    G.edge[0][3] = G.edge[3][0] = INFINITY;
    G.edge[0][4] = G.edge[4][0] = INFINITY;
    G.edge[1][1] = 0;
    G.edge[1][2] = G.edge[2][1] = INFINITY;
    G.edge[1][3] = G.edge[3][1] = 1;
    G.edge[1][4] = G.edge[4][1] = 4;
    G.edge[2][2] = 0;
    G.edge[2][3] = G.edge[3][2] = INFINITY;
    G.edge[2][4] = G.edge[4][2] = 4;
    G.edge[3][3] = 0;
    G.edge[3][4] = G.edge[4][3] = INFINITY;
    G.edge[4][4] = 0;
    for(int i=0; i<G.n; i++) {
        visited[i] = 0;
    }
    printf("邻接矩阵为：\n");
    for (int i = 0; i < G.n; i++) {
        for (int j = 0; j < G.n; j++) {
            printf("%d\t", G.edge[i][j]);
        }
        printf("\n");
    }
    printf("广度优先遍历为：\n");
    BFS(G,4);
    return 0;
}