【图论】最小生成树（python和cpp）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【图论】最小生成树（python和cpp）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、声明

本帖持续更新中
如有纰漏望指正！

二、简介

（a）点云建立的k近邻图	（b）k近邻图上建立的最小生成树

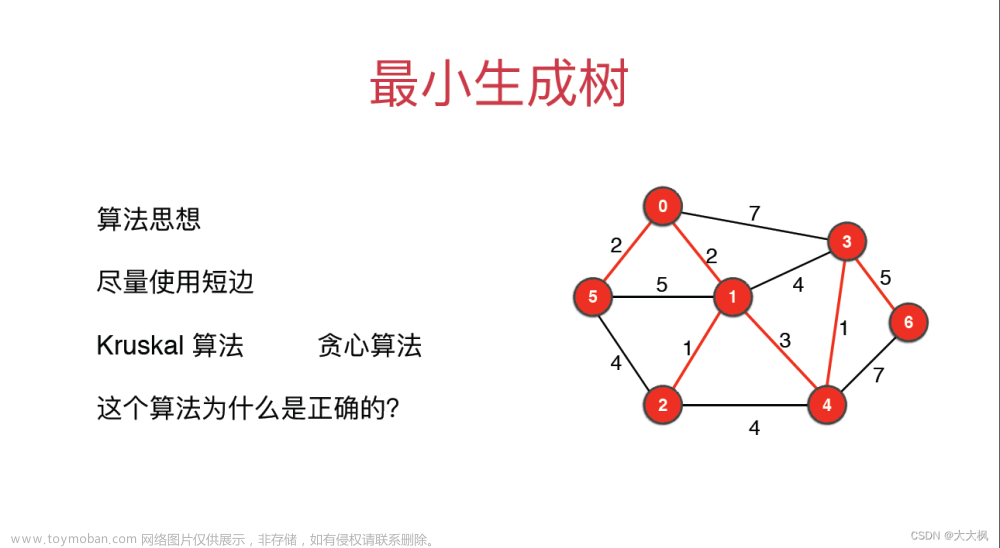
最小生成树 (Minimum Spanning Tree，简称 MST) 是一种在带权无向图中的树，它连接了图中所有节点并且总权重最小。在最小生成树中，任意两个节点之间有且仅有一条路径，同时这些路径的权重之和最小。
最小生成树的应用场景非常广泛。以下是一些常见的应用场景：

网络设计：在计算机网络或通信网络中，最小生成树可以用来构建最优的网络拓扑结构，以便实现高效的数据传输和通信。
物流规划：在物流管理中，最小生成树可以用来确定最短路径，从而有效地规划货物的运输路线，降低物流成本。
电力传输：在电力系统中，最小生成树可以用于确定电力输电线路的布置，确保电力从发电站到各个用户点的传输成本最小。
集群分析：在数据挖掘和机器学习中，最小生成树可以用于聚类分析，帮助发现数据点之间的相关性和相似性。
电路板设计：在电路板设计中，最小生成树可以用来确定电路中的连接线路，以便最小化电路板的制造成本。

最小生成树算法有多种，其中最著名且常用的算法是普里姆算法（Prim’s algorithm）和克鲁斯卡尔算法（Kruskal’s algorithm），它们可以高效地找到最小生成树。文章来源地址https://www.toymoban.com/news/detail-755488.html

三、代码

C++代码

#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/kruskal_min_spanning_tree.hpp>
#include <iostream>
#include <vector>

int main() {
    // Define the graph using adjacency_list
    typedef boost::adjacency_list<boost::vecS, boost::vecS, boost::undirectedS,
        boost::no_property, boost::property<boost::edge_weight_t, int>> Graph;

    typedef boost::graph_traits<Graph>::edge_descriptor Edge;
    typedef boost::property_map<Graph, boost::edge_weight_t>::type WeightMap;

    // Create a graph object
    Graph g;

    // Add edges to the graph
    add_edge(0, 1, 2, g);
    add_edge(1, 2, 3, g);
    add_edge(0, 3, 1, g);
    // ... Add other edges as needed

    // Vector to store the resulting MST edges
    std::vector<Edge> spanning_tree;

    // Compute the minimum spanning tree using Kruskal's algorithm
    boost::kruskal_minimum_spanning_tree(g, std::back_inserter(spanning_tree));

    // Print the edges in the MST
    for (std::vector<Edge>::iterator ei = spanning_tree.begin(); ei != spanning_tree.end(); ++ei) {
        std::cout << source(*ei, g) << " <--> " << target(*ei, g)
                  << " with weight of " << get(boost::edge_weight, g, *ei) << std::endl;
    }

    return 0;
}

Python代码

import open3d as o3d
import numpy as np
import networkx as nx
from scipy.spatial import KDTree

def create_knn_graph(point_cloud, k):
    # Convert Open3D point cloud to numpy array
    points = np.asarray(point_cloud.points)
    
    # Build a KDTree for efficient nearest neighbor search
    tree = KDTree(points)
    
    # Create a graph
    G = nx.Graph()
    
    # Add nodes
    for i in range(len(points)):
        G.add_node(i, pos=points[i])

    # Add edges based on k nearest neighbors
    for i in range(len(points)):
        distances, indices = tree.query(points[i], k=k+1)  # k+1 because the point itself is included
        for j in range(1, k+1):  # Skip the first one (itself)
            G.add_edge(i, indices[j], weight=distances[j])

    return G

def find_mst(graph):
    # Compute the minimum spanning tree
    return nx.minimum_spanning_tree(graph)

# Load point cloud
pcd = o3d.io.read_point_cloud("path_to_your_point_cloud_file.ply") # Adjust the file path

# Create the kNN graph (choose your k)
k = 5  # For example, k=5
knn_graph = create_knn_graph(pcd, k)

# Find the minimum spanning tree
mst = find_mst(knn_graph)

# Optional: Plot the MST
pos = nx.get_node_attributes(mst, 'pos')
nx.draw(mst, pos, with_labels=True, node_size=20, font_size=8)