时间序列分析——基于R（第2版）

这篇具有很好参考价值的文章主要介绍了时间序列分析——基于R（第2版）—第4章。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

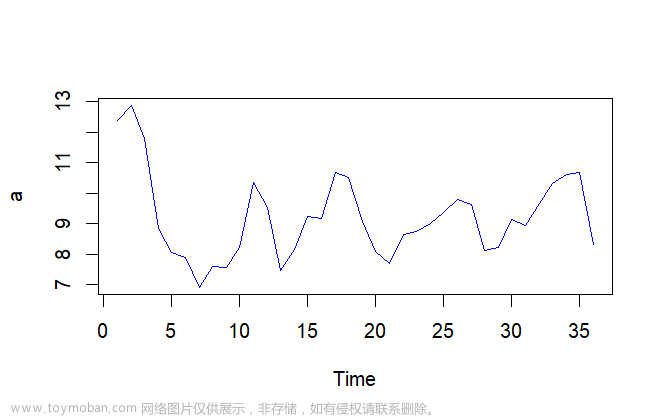
4_1某公司过去50个月每月盈亏

绘制该序列的时序图
判断该序列的平稳性与纯随机性#平稳非白噪声
考察该序列自相关图和偏自相关图的性质
利用拟合模型预测该公司未来5年的盈亏情况

q41=ts(E4_1$x)
plot(q41)#绘制时序图
#library(aTSA)
#adf.test(q41)
for(i in 1:2) print(Box.test(q41,lag=6*i))#白噪声检验
#纯随机性检验 p值<0.05,拒绝原假设，属于非白噪声序列

acf(E4_1$x,lag=50)#绘制自相关图 拖尾
#自相关系数除了延迟1-2阶都在2倍标准差范围内波动，该序列具有短期相关性，可认为序列平稳

pacf(q41,lag=50)#绘制偏自相关图 1阶截尾
#偏自相关图除了1阶都在2倍标准差范围内波动

#根据自相关图 拖尾，偏自相关图一阶截尾属性，拟合为AR(1)模型
q41.fit=arima(q41,order=c(1,0,0))#AR(1)
q41.fit
library(forecast)
q41.fore=forecast(q41.fit,h=60)
plot(q41.fore)

4_2某城市过去四年每个月人口净流入量

绘制该序列的时序图
判断该序列的平稳性与纯随机性#平稳非白噪声
考察该序列自相关图和偏自相关图的性质
选择适当模型拟合该序列的发展
利用拟合模型预测该城市未来5年的人净流入情况

q42=ts(E4_2$x)
plot(q42)#绘制时序图
#library(aTSA)
#adf.test(q42)
Box.test(q42,lag=6)#白噪声检验
#纯随机性检验 p值<0.1,属于非白噪声序列

acf(q42)#自相关图 1阶截尾
#自相关系数除了延迟1阶都在2倍标准差范围内波动，该序列具有短期相关性，序列平稳

pacf(q42)#偏自相关图 拖尾

#根据自相关图1阶截尾，偏自相关图拖尾的属性，拟合为MA(1)模型
q42.fit1=arima(q42,order=c(0,0,1))#MA(1)
q42.fit1
q42.fore=forecast(q42.fit1,h=60)
plot(q42.fore)#5年预测值
q42.fore

#模型显著性检验
for(i in 1:2) print(Box.test(q42.fit1$residual,lag=6*i))
#由于各阶延迟下的LB统计量的P值都显著大于0.05，可认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效

#参数的显著性检验
t1=0.5683/0.1036
pt(t1,df=56,lower.tail = F)#ma1显著性检验,P<0.05,显著非0
t2=3.4313/0.2032
pt(t2,df=56,lower.tail = T)#常数显著性检验,P>0.05,不显著非0
#检验结果显示常数显著性检验未通过，故不选择该模型

library(forecast)
q42.fit2=auto.arima(q42)#自动选择模型
q42.fit2
for(i in 1:2) print(Box.test(q42.fit2$residual,lag=6*i))
#由于各阶延迟下的LB统计量的P值都显著大于0.05，可认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效

#预测
q42.fore=forecast(q42.fit2,h=60)
plot(q42.fore)
q42.fore

4_3某公司过去3年每月缴纳的税收金额

绘制该序列的时序图
判断该序列的平稳性与纯随机性#平稳非白噪声
考察该序列自相关图和偏自相关图的性质
尝试用多个模型拟合该序列的发展，并考察该序列的拟合模型优化问题
利用最优拟合模型预测该公司未来1年的人口死亡率情况

q43=ts(E4_3$x)
plot(q43)#绘制时序图
#library(aTSA)
#adf.test(q43)
for(i in 1:2) print(Box.test(q43,lag=6*i))#白噪声检验
#纯随机性检验 p值<0.05,属于非白噪声序列

acf(q43)#自相关图 拖尾/1阶截尾
#自相关系数除了延迟1阶都在2倍标准差范围内波动，该序列具有短期相关性，序列平稳

pacf(q43)#偏自相关图2阶截尾/拖尾

#自相关图拖尾 偏自相关图2阶截尾拟合为AR(2)模型
q43.fit1=arima(q43,order=c(2,0,0))#AR(2)
q43.fit1
#模型显著性检验
for(i in 1:2) print(Box.test(q43.fit1$residual,lag=6*i))
#由于各阶延迟下的LB统计量的P值都显著大于0.05，可认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效
#参数的显著性检验
t1=1.0276/0.1524
pt(t1,df=56,lower.tail = F)#ar1系数显著性检验，P<0.05,显著非0
t2=-0.5412/0.1738
pt(t2,df=56,lower.tail = T)#ar2系数显著性检验,P<0.05,显著非0
t3=9.1154/0.2945
pt(t3,df=56,lower.tail = F)#常数显著性检验,P<0.05,显著非0
#检验结果显示3个系数均显著非0

#根据自相关图1阶截尾，偏自相关图拖尾的属性，拟合为MA(1)模型
q43.fit2=arima(q43,order=c(0,0,1))#MA(1)
q43.fit2
#模型显著性检验
for(i in 1:2) print(Box.test(q43.fit2$residual,lag=6*i))
#由于各阶延迟下的LB统计量的P值都显著大于0.05，可认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效
#参数的显著性检验
t1=1/0.0798
pt(t1,df=56,lower.tail = F)#ma1系数显著性检验,P<0.05,显著非0
t2=9.2118/0.2792
pt(t2,df=56,lower.tail = F)#常数显著性检验，P<0.05,显著非0
#检验结果显示2个系数均显著非0

#根据自相关图拖尾，偏自相关图拖尾属性，拟合为ARMA(1)模型
q43.fit3=arima(q43,order=c(1,0,1))#ARMA(1,1)
q43.fit3
#模型显著性检验
for(i in 1:2) print(Box.test(q43.fit3$residual,lag=6*i))
#由于各阶延迟下的LB统计量的P值都显著大于0.05，可认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效
#参数的显著性检验
t1=0.4301/0.1629
pt(t1,df=56,lower.tail = F)#ar1系数显著性检验
t2=1/0.0836
pt(t2,df=56,lower.tail = F)#ma1系数显著性检验
t3=9.2189/ 0.4354
pt(t3,df=56,lower.tail = F)#常数显著性检验
#检验结果显示，P值小于0.05，3个系数均显著非0

#优化
AIC(q43.fit1);BIC(q43.fit1)
AIC(q43.fit2);BIC(q43.fit2)
AIC(q43.fit3);BIC(q43.fit3)
#根据AIC和BIC准则，选择ARMA(1,1)为最优模型
library(forecast)
q43.fore=forecast(q43.fit3,h=12)#预测
plot(q43.fore)

4_4某城市过去45年中每年的人口死亡率

绘制该序列的时序图
判断该序列的平稳性与纯随机性#平稳非白噪声
考察该序列自相关图和偏自相关图的性质
尝试用多个模型拟合该序列的发展，并考察该序列的拟合模型优化问题
利用最优拟合模型预测该城市未来5年的人口死亡率情况

q44=ts(E4_4$x)
plot(q44)#绘制时序图 平稳
#时序图在常数附近波动，没有明显的趋势和季节性，基本可视为平稳序列；自相关系数除了延迟1-2阶都在2倍标准差范围内波动，该序列具有短期相关性，可认为序列平稳
#library(aTSA)
#adf.test(q46)
for(i in 1:2) print(Box.test(q44,lag=6*i,type="Ljung-Box"))#白噪声检验
#纯随机性检验 延迟6阶后p值<0.05,满足非随机性，可认为是非白噪声序列

acf(q44,lag=25)#自相关图1阶截尾/拖尾
pacf(q44,lag=25)#偏自相关图 拖尾/2阶截尾

#根据自相关图拖尾，偏自相关图2截尾属性，拟合为AR(2)模型
q44.fit1=arima(q44,order=c(2,0,0))#AR(2)
q44.fit1
#模型显著性检验
for(i in 1:2) print(Box.test(q44.fit1$residual,lag=6*i))
#由于各阶延迟下的LB统计量的P值都显著大于0.05，可认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效
#参数的显著性检验
t1=0.4661/0.1412
pt(t1,df=56,lower.tail = F)#ar1系数显著性检验,P<0.05,显著非0
t2=-0.3259/0.1394
pt(t2,df=56,lower.tail = T)#ar2系数显著性检验，P<0.05,显著非0
t3=4.9569/0.1597
pt(t3,df=56,lower.tail = F)#常数显著性检验,P<0.05,显著非0
#检验结果显示3个系数均显著非0

#根据自相关图1阶截尾，偏自相关图拖尾属性，拟合为MA(1)模型
q44.fit2=arima(q44,order=c(0,0,1))#MA(1)
q44.fit2
#模型显著性检验
for(i in 1:2) print(Box.test(q44.fit2$residual,lag=6*i))
tsdiag(q44.fit2)
#由于各阶延迟下的LB统计量的P值都显著大于0.05，可认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效
#参数的显著性检验
t1=0.4495/0.1203
pt(t1,df=56,lower.tail = F)#ar2系数显著性检验，P<0.05,显著非0
t2=4.9444/0.2020#常数显著性检验，P<0.05,显著非0
pt(t2,df=56,lower.tail = F)#常数显著性检验,P<0.05,显著非0
#检验结果显示2个系数均显著非0

#根据自相关图拖尾，偏自相关图拖尾属性，拟合为ARMA(1,1)模型
q44.fit3=arima(q44,order=c(1,0,1))#ARMA(1,1)
q44.fit3
#模型显著性检验
for(i in 1:2) print(Box.test(q44.fit3$residual,lag=6*i))
#由于各阶延迟下的LB统计量的P值都显著大于0.05，可认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效
#参数的显著性检验
t1=0.0408/0.2593
pt(t1,df=56,lower.tail = F)#ar1系数显著性检验，P>0.05,不显著
t2=0.4220/0.2151
pt(t2,df=56,lower.tail = F)#ma1系数显著性检验
t3=4.9435/ 0.2065
pt(t3,df=56,lower.tail = F)#常数显著性检验
#检验结果显示，只有2个系数均显著非0，不能拒绝参数为0的原假设，故不选择该模型

#优化
AIC(q44.fit1);BIC(q44.fit1)
AIC(q44.fit2);BIC(q44.fit2)
#二者的AIC值差不多，BIC值MA模型更优
#auto.arima(q44)#系统自动定阶与我选择的一致


#预测
library(forecast)
q44.fore=forecast(q44.fit2,h=5)
plot(q44.fore)

4_6 某城市过去63年中每年降雪量

判断该序列的平稳性与纯随机性#平稳非白噪声序列
如果序列平稳且非白噪声，选择适当模型拟合该序列的发展
利用拟合模型预测该城市未来5年的降雪量

q46=ts(E4_6$x)
plot(q46)#绘制时序图

acf(q46)#自相关图 拖尾/2阶截尾
#自相关系数除了延迟1~2阶都在2倍标准差范围内波动，该序列具有短期相关性，序列平稳
#library(aTSA)
#adf.test(q46)
pacf(q46)#偏自相关图拖尾

Box.test(q46,lag=6,type="Ljung-Box")#白噪声检验
#纯随机性检验 p值<0.1,属于非白噪声序列

library(forecast)
q46.fit1=auto.arima(q46)#自动选择
q46.fit1
#模型显著性检验
for(i in 1:2) print(Box.test(q46.fit1$residual,lag=6*i))
#由于各阶延迟下的LB统计量的P值都显著大于0.05，可认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效
#参数的显著性检验
t1=-0.6749/0.1717
pt(t1,df=56,lower.tail = T)#ar1系数显著性检验，P<0.05,显著非0

#预测
q46.fore=forecast(q46.fit1,h=5)
plot(q46.fore)
q46.fore

4_7某地区连续74年的谷物产量

判断该序列的平稳性与纯随机性
选择适当模型拟合该序列的发展
利用拟合模型预测该地区未来5年的谷物产量

q47=ts(E4_7$x)
plot(q47)#绘制时序图
#library(aTSA)
#adf.test(q47)
acf(q47)#自相关图 拖尾
#自相关系数除了延迟1~3阶都在2倍标准差范围内波动，该序列具有短期相关性，序列平稳

pacf(q47)#偏自相关图拖尾

for(i in 1:2) print(Box.test(q47,lag=6*i))#白噪声检验
#纯随机性检验 p值<0.05,属于非白噪声序列

q47.fit1=arima(q47,order=c(1,0,1))#根据自相关和偏自相关拖尾，拟合为ARMA(1，1)模型
q47.fit1
library(forecast)
q47.fore=forecast(q47.fit1,h=5)#利用拟合模型预测该地区未来5年的谷物产量
q47.fore#预测值如下
plot(q47.fore)
q47.fore

#模型显著性检验
for(i in 1:2) print(Box.test(q47.fit1$residual,lag=6*i))
#由于各阶延迟下的LB统计量的P值都显著大于0.05，可认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效
#参数的显著性检验
t1=0.9355/0.0837
pt(t1,df=56,lower.tail = F)#ar1系数显著性检验，P<0.05,显著非0
t2=-0.7266/0.1475#常数显著性检验，P<0.05,显著非0
pt(t2,df=56,lower.tail = T)#ma1显著性检验,P<0.05,显著非0
t3=0.8319/0.1135
pt(t3,df=56,lower.tail = F)#常数显著性检验,P<0.05,显著非0
#检验结果显示3个系数显著非0
AIC(q47.fit1);BIC(q47.fit1)

library(forecast)
q47.fit2=auto.arima(q47)#自动选择为ARIMA(0,1,1)
q47.fit2
#模型显著性检验
for(i in 1:2) print(Box.test(q47.fit2$residual,lag=6*i))
#由于各阶延迟下的LB统计量的P值都显著大于0.05，可认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效
#参数的显著性检验
t1=-0.7966/0.0768
pt(t1,df=56,lower.tail = T)#ma1系数显著性检验，P<0.05,显著非0
AIC(q47.fit2);BIC(q47.fit2)

#根据选择AIC,BIC准则，选择ARIMA(0,1,1)模型效果更好，预测如下
q47.fore=forecast(q47.fit2,h=5)
plot(q47.fore)
q47.fore

4_8 201个连续生产记录

判断该序列的平稳性与陈随机性
如果序列平稳且非白噪声，选择适当的模型拟合该序列的发展
利用拟合模型预测该序列下一时刻95%的置信区间

q48=ts(E4_8$x)
plot(q48)#绘制时序图

acf(q48)#自相关图 1阶截尾
#自相关系数除了延迟1阶都在2倍标准差范围内波动，该序列具有短期相关性，序列平稳

pacf(q48)#偏自相关图拖尾
adf.test(q48)#平稳
for(i in 1:2) print(Box.test(q48,lag=6*i))#白噪声检验
#纯随机性检验 p值<0.05,属于非白噪声序列

#根据自相关图 1阶截尾，偏自相关图拖尾属性，拟合为MA(1)模型
q48.fit=arima(q48,order=c(0,0,1))#MA(1)
library(forecast)
q48.fore=forecast(q48.fit,h=1)#预测
q48.fore
#xt=84.1297+Et-0.4775Et-1
#下一期预测置信区间为80.43481 90.92585

4_9 澳大利亚季度常住人口文章来源地址https://www.toymoban.com/news/detail-756290.html

判断该序列的平稳性与纯随机性
选择适当模型拟合该序列的发展
绘制该序列的拟合图及未来5年预测图

q49=ts(E4_9$x)
plot(q49)#绘制时序图

acf(q49)#自相关图 拖尾
#序列平稳

pacf(q49)#偏自相关图拖尾

for(i in 1:2) print(Box.test(q49,lag=6*i))#白噪声检验
#纯随机性检验 p值<0.05,属于非白噪声序列

q49.fit1=arima(q49,order=c(1,1,1))#拟合为ARIMA(1,1,1)
#模型显著性检验
for(i in 1:2) print(Box.test(q49.fit1$residual,lag=6*i))
#由于12阶延迟下的LB统计量的P值显著大于0.05，可认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效

#参数的显著性检验
q49.fit1
t1=-0.3222/0.118
pt(t1,df=56,lower.tail = T)#ar1系数显著性检验，P<0.05,显著非0
t1=-0.782/0.0707
pt(t1,df=56,lower.tail = T)#ma1系数显著性检验，P<0.05,显著非0
#检验结果显示2个系数显著非0
AIC(q49.fit1);BIC(q49.fit1)

library(forecast)
q49.fit2=auto.arima(q49)#自动选择
q49.fit2
#模型显著性检验
for(i in 1:2) print(Box.test(q49.fit2$residual,lag=6*i))
#由于各阶延迟下的LB统计量的P值都显著大于0.05，可认为这个拟合模型的残差序列属于白噪声序列，即该拟合模型显著有效

#参数的显著性检验
t1=0.1726/0.2276
pt(t1,df=56,lower.tail = F)#ma1系数显著性检验，P>0.05,不显著非0.不选择该模型

#选择#ARIMA(1,1,1)模型，预测
q49.fore=forecast(q49.fit1,h=20)
plot(q49.fore)

到了这里，关于时间序列分析——基于R（第2版）—第4章的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！