动态规划-最长公共子序列(c语言)-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划-最长公共子序列(c语言)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

实验3：最长公共子序列

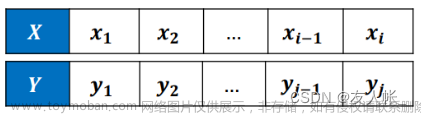
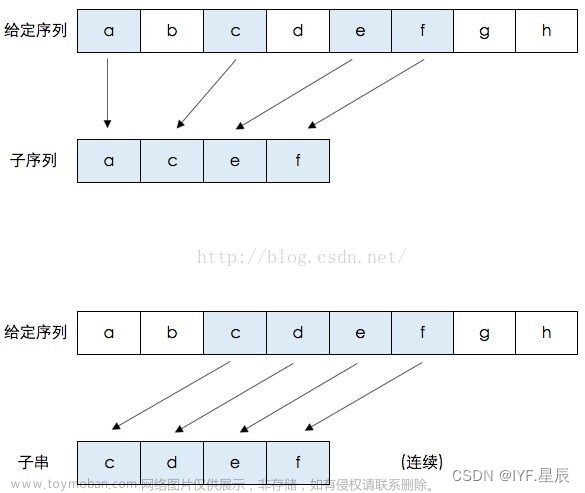
内容：给定两个字符串str1和str2，输出两个字符串的最长公共子序列，如果最长公共子序列为空，则返回“-1”。目前给出的数据，仅仅会存在一个最长的公共子序列。

数据范围：0≤|str1|，|str2|≤2000

要求：空间复杂度O（n2）

具体思路：

step1：dp[i][j]的含义是，以str1中的第i个字符，str2中的第j个字符结尾的最长子序列长度
step2：转移方程，对于dp[i][j]来说，
如果str1[i-1]与str2[j-1]相等，那么dp[i][j]=dp[i-1][j-1]+1,
如果不等，dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
step3：获取公共子序列，从dp数组的最后一个位置开始遍历，如果每次比较当前位置与其左、上、左上的关系，然后将符合要求的字符加入栈中，符合要求即来自dp表格左上方的字符。然后将栈中的字符拼接即可得到最长公共子序列，注意检查子序列是否为空

最长公共子序列问题c语言,动态规划,算法文章来源地址https://www.toymoban.com/news/detail-756428.html

#include <stdio.h>
#include <string.h>
#define MAX 50
char str1[MAX];
char str2[MAX];//两个字符串
int n1,n2;//计字符串长度
int dp[MAX][MAX];
char s[MAX];//存最长序列
int count;//存最长序列的长度
void view();
void LCS();
int max(int a,int b);
int main()
{
    printf("请输入两个字符串\n");
    scanf("%s %s",&str1,&str2);
    n1=strlen(str1);
    n2=strlen(str2);
    LCS();
    view();
    printf("第一个字符串:%s\n第二个字符串：%s\n",str1,str2);
    printf("长度：%d\n",dp[n1][n2]);
    printf("最长子序列：%s\n",s);
    return 0;
}
int max(int a,int b)
{
    return a>b?a:b;
}

void LCS()
{
    //初始化dp数组
    for(int i=0;i<=n1;i++)
    {
        dp[i][0]=0;
    }
    for(int j=0;j<=n2;j++)
    {
        dp[0][j]=0;
    }
    //LCS
    //dp[i][j]=dp[i-1][j-1] (str1[i-1]==str2[j-1])
    //dp[i][j]=max(dp[i-1][j],dp[i][j-1])  (str1[i-1]!=str2[j-1])
    //dp[i][j] 分别是以str1第i个字符结尾，str2第j个字符结尾的最长序列长度
    //           0 1 2
    //例：char[] a b c
    //dp       0 1 2 3......其中0被初始化了
    for(int i=1;i<=n1;i++)
    {
        for(int j=1;j<=n2;j++)
        {
            if(str1[i-1]==str2[j-1])
                dp[i][j]=dp[i-1][j-1]+1;
            else
                dp[i][j]=max(dp[i-1][j],dp[i][j-1]);

        }
    }
}

//看是哪些序列
void view()
{
    int i=n1,j=n2;//倒着看
    count=dp[n1][n2]-1;//序列长度-1
    while(count>=0)
    {
        if(dp[i][j]==dp[i-1][j-1])
        {
            s[count]=str1[i-1];
            count--;
            i--,j--;
        }
        else if(dp[i][j]==dp[i][j-1])
        {
            j--;
        }
        else//dp[i][j]==dp[i-1][j]
        {
            i--;
        }
    }

    }

到了这里，关于动态规划-最长公共子序列(c语言)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！