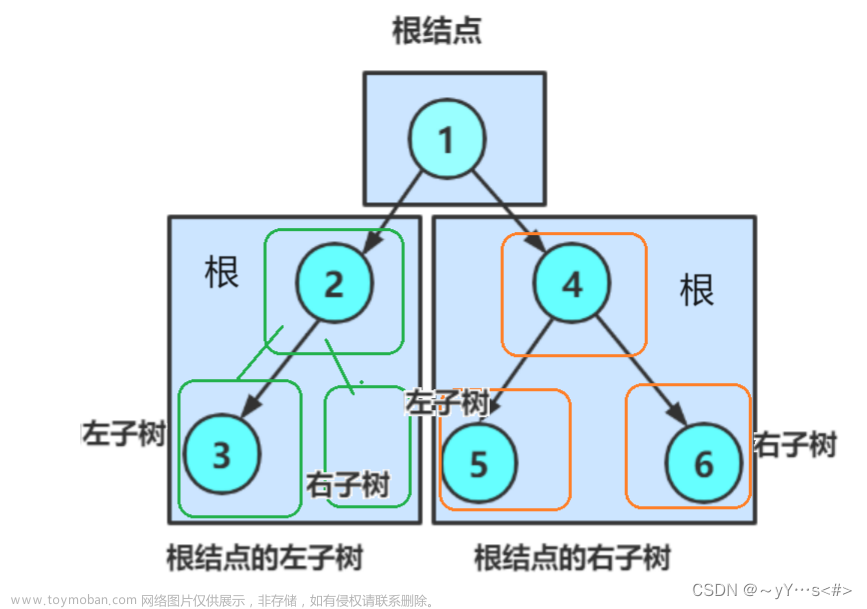
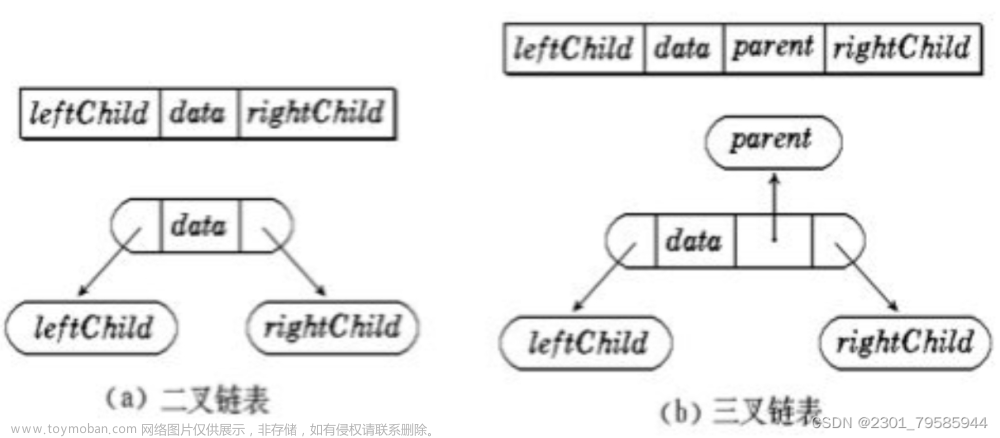
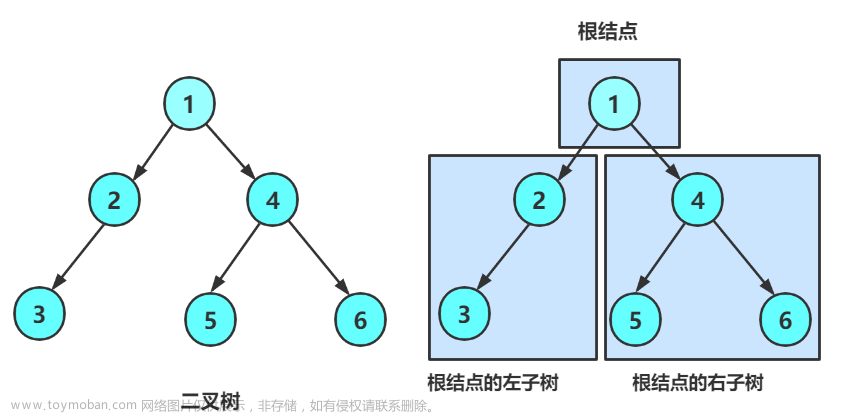
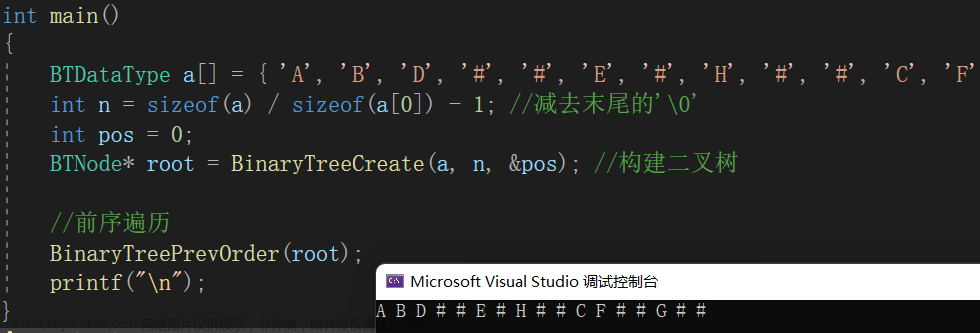
第五章、二叉树的链式存储的实现和基本操作
InitBiTree(BiTree T)——初始化二叉树。
CreateBiTree(BiTree &T)——先序遍历的顺序建立二叉链表。
PreOrderTraverse(BiTree T)——先序遍历。
InOrderTraverse(BiTree T)——中序遍历。
PostOrderTraverse(BiTree T)——后序遍历。
Copy(BiTree T,BiTree &NewT)——复制二叉树。
Depth(BiTree T)——计算二叉树的深度。
NodeCount(BiTree T)——统计二叉树中结点的个数。
NodeCount1(BiTree T)——二叉树T中度为1的结点总数。文章来源:https://www.toymoban.com/news/detail-756614.html
NodeCount2(BiTree T)——二叉树T中度为2的结点总数。文章来源地址https://www.toymoban.com/news/detail-756614.html
二叉树的链式存储的实现代码
//------------二叉树的链式存储的实现-----------//
#include<stdio.h>
#include<iostream>
#include<string>
using namespace std;
//------二叉树的二叉链表存储表示------//
typedef struct BiTNode
{
char data;//结点数据域
struct BiTNode *lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;
//初始化二叉树
void InitBiTree(BiTree T)
{
T=new BiTNode;
T==NULL;
}
//先序遍历的顺序建立二叉链表
void CreateBiTree(BiTree &T)
{
//按先序次序输入二叉树中的结点的值(一个字符),创建二叉链表表示的二叉树T
char ch;
cin>>ch;
if(ch=='#') T=NULL;//递归结束,建空树
else //递归创建二叉树
{
T=new BiTNode;//生成根结点
T->data=ch;
CreateBiTree(T->lchild);//递归创建左子树
CreateBiTree(T->rchild);//递归创建右子树
}
}
//先序遍历
void PreOrderTraverse(BiTree T)
{
if(T)
{
cout<<T->data;//访问根结点
PreOrderTraverse(T->lchild);//先序遍历左子树
PreOrderTraverse(T->rchild);//先序遍历右子树
}
}
//中序遍历
void InOrderTraverse(BiTree T)
{
if(T)
{
InOrderTraverse(T->lchild);//中序遍历左子树
cout<<T->data;//访问根结点
InOrderTraverse(T->rchild);//中序遍历右子树
}
}
//后序遍历
void PostOrderTraverse(BiTree T)
{
if(T)
{
cout<<T->data;
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
}
}
//复制二叉树
void Copy(BiTree T,BiTree &NewT)
{
//复制一棵和T完全相同的二叉树
if(T==NULL)//如果是空树,递归结束
{
NewT=NULL;
return;
}
else
{
NewT=new BiTNode;
NewT->data=T->data;//复制根结点
Copy(T->lchild,NewT->lchild);//递归复制左子树
Copy(T->rchild,NewT->rchild);//递归复制右子树
}
}
//计算二叉树的深度
int Depth(BiTree T)
{
if(T==NULL) return 0;
else
{
int m=Depth(T->lchild);
int n=Depth(T->rchild);
if(m>n)
return m+1;
else
return n+1;
}
}
//统计二叉树中结点的个数
int NodeCount(BiTree T)
{
if(T==NULL)
return 0;
else
return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
}
//求二叉树T中度为1的结点总数
int NodeCount1(BiTree T)
{
if (T == NULL)
{
return 0;
}
else if ((T->lchild == NULL) && (T->rchild == NULL))
{
return 0;
}
else if(T->lchild == NULL)
{
return 1+ NodeCount1(T->rchild);
}
else if (T->rchild == NULL)
{
return 1 + NodeCount1(T->lchild);
}
else
return NodeCount1(T->lchild)+ NodeCount1(T->rchild);
}
//求二叉树T中度为2的结点总数
int NodeCount2(BiTree T)
{
if (T == NULL)
{
return 0;
}
else if ((T->lchild == NULL) && (T->rchild == NULL))
{
return 0;
}
else if (T->lchild == NULL)
{
return NodeCount2(T->rchild);
}
else if (T->rchild == NULL)
{
return NodeCount2(T->lchild);
}
else if ((T->lchild != NULL) && (T->rchild != NULL))
{
return 1+ NodeCount2(T->lchild) + NodeCount2(T->rchild);
}
}
void Menu()
{
printf("*************************************\n");
printf("1.二叉树的初始化\n");
printf("2.建立二叉树\n");
printf("3.中序遍历\n");
printf("4.后序遍历\n");
printf("5.复制二叉树\n");
printf("6.二叉树的深度\n");
printf("7.二叉树中结点的个数\n");
printf("8.二叉树T中度为1的结点总数\n");
printf("9.二叉树T中度为2的结点总数\n");
printf("10.退出程序\n");
printf("*************************************\n");
}
int main()
{
int choice;
BiTree T,NewT;
char ch;
while(1)
{
Menu();
printf("请输入要执行的操作:");
scanf("%d",&choice);
switch(choice)
{
case 1:
InitBiTree(T);
printf("二叉树T初始化成功!\n");
break;
case 2:
printf("请输入要创建的二叉树,按先序序列输入,空树用字符'#'代替:");
CreateBiTree(T);
printf("二叉树T创建成功!\n");
printf("此时前序遍历二叉树为:");
PreOrderTraverse(T);
printf("\n");
break;
case 3:
printf("中序遍历二叉树为:");
InOrderTraverse(T);
printf("\n");
break;
case 4:
printf("后序遍历二叉树为:");
PostOrderTraverse(T);
printf("\n");
break;
case 5:
printf("复制后的二叉树为(先序遍历):");
Copy(T,NewT);
PreOrderTraverse(T);
printf("\n");
break;
case 6:
Depth(T);
printf("二叉树T的深度为:%d\n",Depth(T));
break;
case 7:
NodeCount(T);
printf("二叉树中结点的个数为:%d\n",NodeCount(T));
break;
case 8:
NodeCount1(T);
printf("二叉树T中度为1的结点总数为:%d\n",NodeCount1(T));
break;
case 9:
NodeCount2(T);
printf("二叉树T中度为2的结点总数为:%d\n",NodeCount2(T));
break;
case 10:
printf("退出程序!");
exit(0);
break;
default:
printf("输入错误!");
break;
}
}
} 运行结果
*************************************
1.二叉树的初始化
2.建立二叉树
3.中序遍历
4.后序遍历
5.复制二叉树
6.二叉树的深度
7.二叉树中结点的个数
8.二叉树T中度为1的结点总数
9.二叉树T中度为2的结点总数
10.退出程序
*************************************
请输入要执行的操作:1
二叉树T初始化成功!
*************************************
1.二叉树的初始化
2.建立二叉树
3.中序遍历
4.后序遍历
5.复制二叉树
6.二叉树的深度
7.二叉树中结点的个数
8.二叉树T中度为1的结点总数
9.二叉树T中度为2的结点总数
10.退出程序
*************************************
请输入要执行的操作:2
请输入要创建的二叉树,按先序序列输入,空树用字符'#'代替:ABC##DE#G##F###
二叉树T创建成功!
此时前序遍历二叉树为:ABCDEGF
*************************************
1.二叉树的初始化
2.建立二叉树
3.中序遍历
4.后序遍历
5.复制二叉树
6.二叉树的深度
7.二叉树中结点的个数
8.二叉树T中度为1的结点总数
9.二叉树T中度为2的结点总数
10.退出程序
*************************************
请输入要执行的操作:3
中序遍历二叉树为:CBEGDFA
*************************************
1.二叉树的初始化
2.建立二叉树
3.中序遍历
4.后序遍历
5.复制二叉树
6.二叉树的深度
7.二叉树中结点的个数
8.二叉树T中度为1的结点总数
9.二叉树T中度为2的结点总数
10.退出程序
*************************************
请输入要执行的操作:4
后序遍历二叉树为:ABCDEGF
*************************************
1.二叉树的初始化
2.建立二叉树
3.中序遍历
4.后序遍历
5.复制二叉树
6.二叉树的深度
7.二叉树中结点的个数
8.二叉树T中度为1的结点总数
9.二叉树T中度为2的结点总数
10.退出程序
*************************************
请输入要执行的操作:5
复制后的二叉树为(先序遍历):ABCDEGF
*************************************
1.二叉树的初始化
2.建立二叉树
3.中序遍历
4.后序遍历
5.复制二叉树
6.二叉树的深度
7.二叉树中结点的个数
8.二叉树T中度为1的结点总数
9.二叉树T中度为2的结点总数
10.退出程序
*************************************
请输入要执行的操作:6
二叉树T的深度为:5
*************************************
1.二叉树的初始化
2.建立二叉树
3.中序遍历
4.后序遍历
5.复制二叉树
6.二叉树的深度
7.二叉树中结点的个数
8.二叉树T中度为1的结点总数
9.二叉树T中度为2的结点总数
10.退出程序
*************************************
请输入要执行的操作:7
二叉树中结点的个数为:7
*************************************
1.二叉树的初始化
2.建立二叉树
3.中序遍历
4.后序遍历
5.复制二叉树
6.二叉树的深度
7.二叉树中结点的个数
8.二叉树T中度为1的结点总数
9.二叉树T中度为2的结点总数
10.退出程序
*************************************
请输入要执行的操作:8
二叉树T中度为1的结点总数为:2
*************************************
1.二叉树的初始化
2.建立二叉树
3.中序遍历
4.后序遍历
5.复制二叉树
6.二叉树的深度
7.二叉树中结点的个数
8.二叉树T中度为1的结点总数
9.二叉树T中度为2的结点总数
10.退出程序
*************************************
请输入要执行的操作:9
二叉树T中度为2的结点总数为:2
*************************************
1.二叉树的初始化
2.建立二叉树
3.中序遍历
4.后序遍历
5.复制二叉树
6.二叉树的深度
7.二叉树中结点的个数
8.二叉树T中度为1的结点总数
9.二叉树T中度为2的结点总数
10.退出程序
*************************************
请输入要执行的操作:10
退出程序!
--------------------------------
Process exited after 46.03 seconds with return value 0
请按任意键继续. . .到了这里,关于数据结构——二叉树的链式存储的实现的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!