💕"活着是为了活着本身而活着"💕
作者:Mylvzi
文章主要内容:数据结构之Map/Set讲解+硬核源码剖析
一.搜索树
1.概念
二叉搜索树又叫二叉排序树,他或者是一颗空树,或者是具有以下性质的树
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
简单来说,二叉搜索树上存储结点的值满足以下条件:
left < root < right
注意:二叉搜索树中不能存在两个相同的值
2.二叉搜索树的操作及其实现
前提准备
static class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
private TreeNode root = null;1.查询操作(search)
根据二叉搜索树的性质很容易实现查询的操作

代码实现:
// search
public boolean search(int val) {
TreeNode cur = root;
while(cur != null) {
if(cur.val < val) {
cur = cur.right;
} else if (cur.val > val) {
cur = cur.left;
}else {
return true;
}
}
return false;
}2.插入操作(insert)
让cur走到合适的位置,再去判断parent.val 与 val的关系,进行插入
画图分析:

代码实现:
// insert
public boolean insert(int val) {
TreeNode newNode = new TreeNode(val);
// 空树直接插入
if (root == null) {
root = newNode;
return true;
}
// 保留cur的根节点
TreeNode parent = null;
TreeNode cur = root;
while(cur != null) {
parent = cur;
if(cur.val < val) {
cur = cur.right;
} else if(cur.val > val){
cur = cur.left;
}else {
// 二叉搜索树中不能存在两个相同的数字
return false;
}
}
// 此时cur就是要插入的位置
if(parent.val < val) {
parent.right = newNode;
}else {
parent.left = newNode;
}
return true;
}3.删除操作(remove)
如果你要删除的cur的结点只有一个子节点,此时删除十分容易

但是如果你想要删除的结点有两个子节点,处理稍微麻烦,因为在你删除cur结点之后,还要保证剩下的结点也满足二叉搜索树的性质,这里采用“替罪羊”法解决删除拥有两个子节点的结点

思路分析:
我现在想要删除90这个结点,但是删除之后谁来替代这个结点呢?
根据二叉搜索树的性质,90看作根节点,则他一定比左树的所有结点的值大,比右树所有结点的值小
我们需要找一个合理的结点去替换90,替换之后仍要满足二叉搜索树的性质,这个合理的结点可以通过两个方法实现
- 找左树的最大值
- 找右树的最小值
现在以找右树的最小值为例演示

代码实现
public void remove(int val) {
TreeNode parent = null;
TreeNode cur = root;
while(cur != null) {
parent = cur;
if (cur.val < val) {
cur = cur.right;
} else if (cur.val > val) {
cur = cur.left;
}else {
removeNode(parent,cur);
return;
}
}
}
private void removeNode(TreeNode parent, TreeNode cur) {
// 注意此时cur就是我要删除的数据
// cur的左树为空
if(cur.left == null) {
if (cur == root) {
root = cur.right;
} else if (cur == parent.left) {
parent.left = cur.right;
}else {
parent.right = cur.right;
}
} else if (cur.right == null) {
// cur的右树为空
if (cur == root) {
root = cur.left;
} else if (cur == parent.left) {
parent.left = cur.left;
}else {
parent.right = cur.left;
}
}else {// 都不等于Null
// 找右树的最小值
// 使用替罪羊法
/* TreeNode targetParent = cur;
TreeNode target = cur.right;
// 找右树的最小值 直到某个结点的left为null 则此节点就是右树最左边的结点 也就是右树的最小值
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if (target == targetParent.left) {
targetParent.left = target.right;
}else {
targetParent.right = target.right;
}*/
// 求左树的最大值
TreeNode tp = cur;
TreeNode t = cur.left;
while (t.right != null) {
tp = t;
t = t.right;
}
// 此时t就是左树的最大值
cur.val = t.val;
// 重写链接
if (t == tp.left) {
tp.left = t.left;
}else {
tp.right = t.left;
}
}
}3.性能分析
对于二叉搜索树来说,进行插入/删除操作都要先进行查询,所以二叉搜索树的性能取决于查询的效率 最好情况是二叉树是一颗完全二叉树 最坏情况则是二叉树是一颗单分支的二叉树

问题:如果是单分支的情况,二叉搜索树的效率会变得很低,如何解决这种问题呢?

4.和 java 类集的关系
TreeMap 和 TreeSet 即 java 中利用搜索树实现的 Map 和 Set;实际上用的是红黑树,而红黑树是一棵近似平衡的 二叉搜索树,即在二叉搜索树的基础之上 + 颜色以及红黑树性质验证,关于红黑树的内容后序再进行讲解。
二.搜索
1.概念和场景
Map和Set是一种专门用来进行“搜索”的数据结构/容器,其搜索效率取决于其具体实现的子类

我们之前其实也学过搜索
1.直接遍历 最粗暴的搜索方法 时间复杂度0(N)
2.二分查找 需要序列是有序的 时间复杂度O(logN)
上述查找适合静态的查找,即在查找的过程中不会进行插入和删除的操作,但是现实中的很多查找都需要动态的进行插入和删除,比如:
1.根据学号查成绩
2.根据通讯录名字查找电话号
3.根据身高找女朋友(bushi)
......
在查找的过程中可能会出现插入和删除的操作,Map和Set就是用于动态的插入和删除的搜索容器
2.搜索的模型
搜索的方式其实有两种,一种是直接在一大堆数据中寻找,另一种是根据对应关系进行查找(比如你需要先找到通讯录的名字,才能根据通讯录的名字找到你要寻找的手机号),我们一般把搜索的数据称为关键字Key,key对应的称为值Value,将其称之为Key-value的键值对
1. 纯 key 模型(找有没有)
- 在词典中找单词
2. Key-Value 模型(找对应关系)
- 梁山好汉的江湖绰号:每个好汉都有自己的江湖绰号
- 学号对应着你的名字
而Map中存储的是Key-Value 模型,Set中存储的是纯 key 模型
三.Map的使用
先放一张Java中和数据结构有关的类的图

1.概念
Map是一个接口类,不能直接实例化对象,如果要使用,需要根据实现他的类来实例化具体的对象,比如TreeMap(底层是红黑树)和HashMap(底层是哈希表)
2.常用方法
1.put
在Map中添加key与value的映射关系
// 根据实现Map的类TreeMap来实例化一个对象
Map<String,Integer> map = new TreeMap<>();
// Put方法
// 设置 单词--出现的次数 这样的一个key与value的映射
map.put("apple",14);
map.put("bank",15);
map.put("cat",17);注意:
1.我们知道,TreeMap的底层是一颗红黑树,存储的时候是使用结点来存储元素的,它实际上存储的是Key-Value的映射关系,实际上Map中存在一个内部类Map.Entry,用于表示映射关系

2.既然TreeMap是一种红黑树,那他在存入数据的时候必然要排序,排序的根据是Key


2.get方法
存在两个get方法 但都是为了返回key对应的value值

System.out.println(map.get("apple"));// 输出14
System.out.println(map.get("bank"));// 输出15
System.out.println(map.get("cat"));// 输出17
// get时进行判断 如果Map中含有传入的key就返回其value 没有则返回其默认值(解某些题很有用)
System.out.println(map.getOrDefault("apple", 100));// 输出14 因为Map中含有apple
System.out.println(map.getOrDefault("Dog", 100));// 输出100 因为Map中不含有Dogget和getOrDefault的源码
// get也可以用来判断是否包含相应的key
public V get(Object key) {
TreeMap.Entry<K,V> p = getEntry(key);
return (p==null ? null : p.value);
}
default V getOrDefault(Object key, V defaultValue) {
V v; // 三目运算符 为真返回v 为假返回默认值
return (((v = get(key)) != null) || containsKey(key))
? v
: defaultValue;
}3.remove
删除key对应的映射关系
源码:注意remove存在返回值
// remove存在返回值!!! 返回你要删除的key对应的value
public V remove(Object key) {
TreeMap.Entry<K,V> p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
deleteEntry(p);
return oldValue;
}验证
System.out.println(map.remove("cat"));// 输出17
System.out.println(map.remove("Dog"));// 输出null4.contains
包含两个contains方法,一个是判断是否存在key,一个判断是否存在value

System.out.println(map.containsKey("cat"));// 输出true
System.out.println(map.containsKey("Dog"));// 输出false
System.out.println(map.containsValue(15));// 输出true
System.out.println(map.containsValue(100));// 输出false源码
public boolean containsKey(Object key) {
return getEntry(key) != null;
}
public boolean containsValue(Object value) {
for (Entry<K,V> e = getFirstEntry(); e != null; e = successor(e))
if (valEquals(value, e.value))
return true;
return false;
}
5.keySet方法
返回不重复的key的集合 就是将Map中所有的key值存放到Set内部(存的时候会进行排序)
// 此处Set里面存放的类型要和key一致!!!
Set<String> set = map.keySet();
for (String s:set) {
System.out.print(s + " ");// 输出apple bank cat
}源码
public Set<K> keySet() {
return navigableKeySet();
}
/**
* @since 1.6
*/
public NavigableSet<K> navigableKeySet() {
KeySet<K> nks = navigableKeySet;
return (nks != null) ? nks : (navigableKeySet = new KeySet<>(this));
}6.values
返回所有的value的可重复集合 和上一个方法类似 此方法是拿到所有的value将其存放到Collection里面
Collection<Integer> collection = map.values();
for (int val:collection) {
System.out.print(val + " ");// 输出14 15 17
}源码
public Collection<V> values() {
Collection<V> vs = values;
if (vs == null) {
vs = new Values();
values = vs;
}
return vs;
}7.entrySet方法
返回所有的key--value的映射关系 可以理解为keySet和values的集合版本

Set<Map.Entry<String,Integer>> set = map.entrySet();
for (Map.Entry<String,Integer> entry:set) {
System.out.println("key = " + entry.getKey() + " " +"value = " + entry.getValue());
}
// 也可以直接打印
System.out.println(set); // 输出[apple=14, bank=15, cat=17]
注意:getKey和getValue是Map的内部类Entry中的方法 用于返回映射中的key和value,所以entrySet方法就相当于创建的Set集合中存储是一个一个Entry

注意:
1.Map是一个接口,只能实例化实现他的类,如TreeMap和HashMap,区别在于前者的底层是二叉搜索树,后者的底层是哈希表
2.Map中存放的key是唯一的(二叉搜索树中不能存放相同的值,哈希表中也不能存放相同的值)
3.在TreeMap中插入键值对时,key不能为空,否则就会抛NullPointerException异常,因为每次put一个元素都需要进行一次比较,而null不能直接比较,value可以为空。但 是HashMap的key和value都可以为空
4.利用keySet方法可以将所有的key分离出来(存放到set里),利用values方法可以将所有的value分离出来(存放到Collection内部)
5.Map中的key不能直接修改,value可以修改(会直接被替换为新值,在二叉搜索树的put代码中就有)
四.set的使用
1.概念
Set是一种纯key模型的数据集合容器 Set是继承自Collection的接口类,也就是Set中不存在values
2.常用方法

3.注意事项:
1.TreeSet的底层其实是TreeMap,所以TreeSet无法存放相同的key值

2.Set实现了toString方法,可以直接打印
Set<String> set = new TreeSet<>();
set.add("lvzi");
set.add("biandu");
set.add("zhizi");
System.out.println(set);// 输出[biandu, lvzi, zhizi]3.Set最大的功能就是对集合中的元素进行去重
4.实现Set接口的常用类有TreeSet和HashSet,还有一个LinkedHashSet,LinkedHashSet是在HashSet的基础 上维护了一个双向链表来记录元素的插入次序。
5.TreeSet中不能插入null的key,HashSet可以
五.哈希表
1.概念
1.什么是哈希表
在顺序结构和平衡二叉树的存储结构中,如果想要搜索某个元素,必须要进行关键码(key)的多次比较,顺序结构的搜索效率是O(N),平衡二叉树的搜索效率是O(logN),搜索的效率取决于比较的次数,,其实之所以需要比较是因为关键码(key)和值(val)之间没有一一对应的关系,如果建立一种关键码与存储位置一一对应的映射,那么我们就能不进行比较就拿到我们需要的数据。比如,,对于一个正比例函数,x与y之间是一一对应的,可以说y与x建立了一一对应的映射关系。
在计算机中,也有这样的一种数据结构,叫做哈希表,实现了关键码和存储位置的一一映射
这种映射关系通过哈希函数(hashFunc)建立(就像正比例函数建立x与y的映射关系一样)
比如:哈希函数设置为:hash(key) = key % capacity; capacity为存储元素底层空间总的大小。

2.哈希冲突
如上图,如果我们再存储一个14,14%10 = 4,他的索引应该是4,但是4下标对应关键字key,不能再对应14了,此时就发生了哈希冲突
3.负载因子
α = 填入表中的元素 / 哈希表的长度

负载因子α用于定性描述冲突率,研究表明,负载因子越大,发生哈希冲突的概率就越大;负载因子越小,发生哈希冲突的概率就越小
2.常见的哈希函数
1.直接定制法
利用关键字的特性建立线性函数,实现关键字和存储位置的一一对应!
适用于数据简单,连续的情况

相关面试题:
387. 字符串中的第一个唯一字符 - 力扣(LeetCode)
思路分析

代码实现
// 1.使用计数数组
class Solution {
public int firstUniqChar(String s) {
int[] cnt = new int[26];
for (int i = 0; i < s.length(); i++) {
cnt[s.charAt(i) - 'a']++;
}
for (int i = 0; i < s.length(); i++) {
if(cnt[s.charAt(i) - 'a'] == 1) {
return i;
}
}
return -1;
}
}
2.// 使用哈希表
Map<Character,Integer> map = new HashMap<>();
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
// 先获取ch的val 无论是否存在 是要val+1 不存在 设置默认值为0 更新后变为1
map.put(ch,map.getOrDefault(ch,0)+1);
}
for (int i = 0; i < s.length(); i++) {
if(map.get(s.charAt(i)) == 1) {
return i;
}
}
return -1;
2.其他
当然还有其他方法,这里仅作了解即可
2. 除留余数法--(常用) 设散列表中允许的地址数为m,取一个不大于m,但最接近或者等于m的质数p作为除数,按照哈希函数: Hash(key) = key% p(p<=m),将关键码转换成哈希地址
3. 平方取中法--(了解) 假设关键字为1234,对它平方就是1522756,抽取中间的3位227作为哈希地址; 再比如关键字为4321,对 它平方就是18671041,抽取中间的3位671(或710)作为哈希地址 平方取中法比较适合:不知道关键字的分 布,而位数又不是很大的情况
4. 折叠法--(了解) 折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些),然后将这几部分叠加求和, 并按散列表表长,取后几位作为散列地址。
折叠法适合事先不需要知道关键字的分布,适合关键字位数比较多的情况
5. 随机数法--(了解) 选择一个随机函数,取关键字的随机函数值为它的哈希地址,即H(key) = random(key),其中random为随机数 函数。 通常应用于关键字长度不等时采用此法
6. 数学分析法--(了解) 设有n个d位数,每一位可能有r种不同的符号,这r种不同的符号在各位上出现的频率不一定相同,可能在某 些位上分布比较均匀,每种符号出现的机会均等,在某些位上分布不均匀只有某几种符号经常出现。可根据 散列表的大小,选择其中各种符号分布均匀的若干位作为散列地址。例如: 假设要存储某家公司员工登记表,如果用手机号作为关键字,那么极有可能前7位都是 相同的,那么我们可以 选择后面的四位作为散列地址,如果这样的抽取工作还容易出现 冲突,还可以对抽取出来的数字进行反转(如 1234改成4321)、右环位移(如1234改成4123)、左环移位、前两数与后两数叠加(如1234改成12+34=46)等方 法。 数字分析法通常适合处理关键字位数比较大的情况,如果事先知道关键字的分布且关键字的若干位分布较均 匀的情况
哈希函数设置的越巧妙,越能减少哈希冲突,但无法避免哈希冲突
那如何解决哈希冲突呢?常用的方法有两种:开散列和闭散列
3.哈希冲突的解决
1.闭散列
也叫开放定址法,当遇到哈希冲突时,如果此时哈希表未满,则证明一定有下标未填充数据,可以将发生哈希冲突的数据填入到空位,所以闭散列的关键是寻找空位,寻找空位有两种方式:线性探测和二次探测
1.线性探测
所谓的线性探测就是从发生冲突的位置开始,依次向后寻找空位
- 先利用哈希函数获得元素的插入位置,
- 如果为空直接插入;不为空,进行线性探测

2.二次探测
线性探测是从发生冲突的位置依次向后寻找空位,可能会导致数据过于集中,为了避免这种情况,可以采用二次探测来寻找空位

研究表明:当表的长度为质数且表装载因子a不超过0.5时,新的表项一定能够插入,而且任何一个位置都不 会被探查两次。因此只要表中有一半的空位置,就不会存在表满的问题。在搜索时可以不考虑表装满的情 况,但在插入时必须确保表的装载因子a不超过0.5,如果超出必须考虑增容
无论是二次探测还是线性探测,都需要开辟大量的空间来解决哈希冲突,所以通过闭散列的方式来解决哈希冲突会导致空间利用率不高,更合理的解决哈希冲突的方式是开散列,也是Java中JDK的解决方式
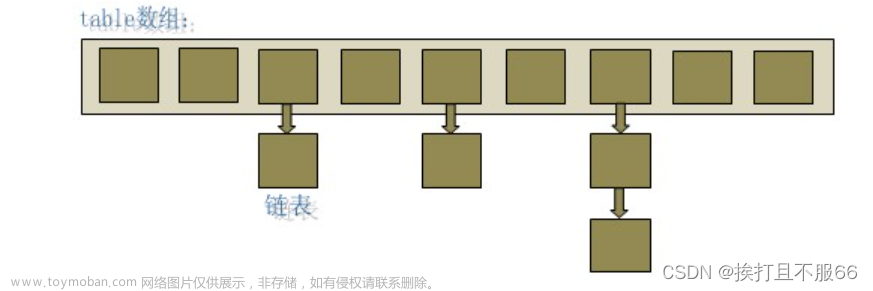
2.开散列(重点)
1.概念
开散列是通过"哈希桶"的方式来解决哈希冲突的,所谓的哈希桶,就是一个特殊的数组,数组的每个元素都是链表
这样,就算发生了哈希冲突,即产生了相同的下标,不需要再去探测空位置,而是在当前位置插入,形成一个链表,搜索数据时需要先定位到下标,再去遍历下标位置对应的整个链表,知道找到要搜索的数据

注意:
如果同时满足数组的长度 > 64 && 链表的长度 > 8 此时性能就会下降,可以通过红黑树来提高性能
2.哈希桶的模拟实现
1.当存储的数据是整数(Key的数据类型为Integer)
前期准备:
// 哈希表实际上一个数组 数组的元素是Node
static class Node {
public int key;
public int val;
public Node next;
public Node(int key, int val) {
this.key = key;
this.val = val;
}
}
public Node[] arr;
public int usedSize;
public HashBuck() {
arr = new Node[5];
}1.search
寻找哈希表中是否存在某个元素,存在返回true,不存在返回false;
public boolean search(int key) {
int index = key % arr.length;
Node cur = arr[index];
while (cur != null) {
if (cur.key == key) {
return true;
}
}
return false;
}2.put
向哈希表中插入数据 需要先判断是否已经存在要插入的元素 如果存在更新val;不存在,直接插入(哈希表中不能存放两个相同的key)
同时,随着哈希表中的数据增多,要去判断冲突因子的是否合理,当同时满足数组的长度 > 64 && 链表的长度 > 8时,需要重新更新哈希表的长度,来降低负载因子的大小,降低哈希冲突;更新长度需要重新哈希,因为可能发生数据的移动
// put方法
public void put(int key,int val) {
int index = key % arr.length;
Node cur = arr[index];
// 遍历整个链表 看是否已经存在相同的key值
while (cur != null) {
if (cur.key == key) {
cur.val = val;
return;
}
cur = cur.next;
}
// 头插法 arr[index]其实就是链表的头节点
Node newNode = new Node(key,val);
newNode.next = arr[index];
arr[index] = newNode;
usedSize++;
// 判断负载因子此时是否合理
if(loadFactor() >= 0.75) {
resize();
}
}
private double loadFactor() {
return usedSize*1.0 / arr.length;
}
private void resize() {
// 扩大到原来的两倍
Node[] tmpArr = new Node[arr.length*2];
// 扩容之后 要进行重新哈希
for (int i = 0; i <arr.length ; i++) {
Node cur = arr[i];
while (cur != null) {
Node curNext = cur.next;
int newIndex = cur.key % tmpArr.length;
// 头插
cur.next = tmpArr[newIndex];
tmpArr[newIndex] = cur;
cur = curNext;
}
}
//数组是对象!!!
arr = tmpArr;
}
3.get
返回关键码Key对应的value 如果不存在返回-1
// get
public int get(int key) {
int index = key % arr.length;
Node cur = arr[index];
while (cur != null) {
if(cur.key == key) {
return cur.val;
}
cur = cur.next;
}
return -1;
}2.数据类型是引用类型
1.前提准备
创建person类
/**
* 数据类型是引用类型 即Key是引用
* 建立引用类Person 与 与 id的映射关系
*/
class Person {
public String id;
public Person(String id) {
this.id = id;
}
// 存储的对象是一个一个人 key是一个引用类型 想要将类型转化为整数 并比较大小 重写方法
@Override
public boolean equals(Object object) {
if (this == object) return true;
if (object == null || getClass() != object.getClass()) return false;
Person person = (Person) object;
return id == person.id;
}
@Override
public int hashCode() {
return Objects.hash(id);
}
}// K,V都是泛型 一定要在类的声明中添加
static class Node<K,V> {
public K key;
public V val;
public Node<K,V> next;
public Node(K key, V val) {
this.key = key;
this.val = val;
}
}
public Node<K,V>[] arr;
public int usedSize;
public HashBuck2() {
arr = (Node<K, V>[]) new Node[5];
}2.put
对于Person类来说,不能直接让他%length来获取他的下标,只能通过hashCode来获取其hash值,再让hash值取%length,从而获取他的下标
// put在hash中插入数据
public void put(K key, V val) {
// 先获取对应的hash值
int hash = key.hashCode();
int index = hash % arr.length;
Node<K,V> cur = arr[index];
while (cur != null) {
if(cur.key.equals(key)) {
cur.val = val;
return;
}
cur = cur.next;
}
Node<K,V> newNode = new Node<>(key,val);
newNode.next = arr[index];
arr[index] = newNode;
usedSize++;
// 判断负载因子此时是否合理
if(loadFactor() >= 0.75) {
resize();
}
}
private double loadFactor() {
return usedSize*1.0 / arr.length;
}
private void resize() {
// 扩大到原来的两倍
Node<K,V>[] tmpArr = new Node[arr.length*2];
// 扩容之后 要进行重新哈希
for (int i = 0; i <arr.length ; i++) {
Node cur = arr[i];
while (cur != null) {
Node curNext = cur.next;
int newIndex = cur.key.hashCode() % tmpArr.length;
// 头插
cur.next = tmpArr[newIndex];
tmpArr[newIndex] = cur;
cur = curNext;
}
}
//数组是对象!!!
arr = tmpArr;
}3.get
// get 根据key获得他的val
public V get(K key) {
int hash = key.hashCode();
int index = hash % arr.length;
Node<K,V> cur = arr[index];
while(cur != null) {
if(cur.key.equals(key)) {
return cur.val;
}
cur = cur.next;
}
return null;
}
4.测试
public static void main(String[] args) {
Person person1 = new Person("123");
Person person2 = new Person("123");
HashBuck2<Person,String> hashBuck2 = new HashBuck2<>();
hashBuck2.put(person1,"lvzi");
// 输出相同的结果 因为Person中重写了equals和hashcode方法 只要内容相同 就认为他们是相同的且具有相同的hashcode值
// get方法就是根据hashcode方法得到hashcode
System.out.println(hashBuck2.get(person1));// 输出lvzi
System.out.println(hashBuck2.get(person2));// 输出lvzi
}注意:
1.在链表中插入数据时有两种方法,头插或尾插jdk1.8之前采用的是头插,1.8之后采用的是尾插
2.哈希表的所有方法的时间复杂度都是O(1),获取index,遍历链表,链表的长度一定是常数的,因为有loadFactor的调节,链表长度过长,会使用红黑树来调整
3.对于引用类型来说,要重写equals和hashCode方法;重写equals方法是因为在比较的时候需要通过内容来进行比较;重写hashCode方法,便于利用数字定位类,也便于我们进行存储
4.equals方法和hashCode方法往往是要同时重写的,这是因为在使用哈希表等数据结构时要保证搜索的一致性
- 如果两个对象通过equals比较返回true,则他们的hashCode值应该相同
- 如果两个对象通过equals比较返回false,则他们的hashCode值不必须一定不同,但为了检索的效率,一般设置为不同
equals方法和hashCode方法的区别

六.hashMap的一些源码讲解
1.成员变量讲解
// 默认容量是16
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
// 最大容量
static final int MAXIMUM_CAPACITY = 1 << 30;
// 负载因子
static final float DEFAULT_LOAD_FACTOR = 0.75f;以上三个都很好理解,下面看几个较为重要但又陌生的成员变量
// 树化条件 每个链表中的结点>=8
static final int TREEIFY_THRESHOLD = 8;
// 解树化条件
static final int UNTREEIFY_THRESHOLD = 6;
// 最小的树华条件 哈希表的容量最小是64
static final int MIN_TREEIFY_CAPACITY = 64;
2.构造方法
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
}
为什么哈希表的容量一定要是2的次幂呢?主要有以下两方面原因:
- 效率性能方面:在建立映射的过程中,最重要的一步在于获取到要插入数据的下标,在上述的模拟实现中,我们采用的是 hash % arr.length()的方法,但还有另一种更快的方法,就是使用位运算,当哈希表的容量n为2的次幂时 ,hash % n == hash &(n-1),这两种求下标的方式是等价的,使用&运算,可以大大提高运算速度
- 哈希函数与桶的关系:使用hash &(n-1)这种方式来获取下标还可以使元素分布更加均匀,降低哈希碰撞的可能性
当n为2的次幂时(4,16,32,64......)时,n-1就是一个每个二进制位都为1的特殊二进制数(15--1111),再通过hash & (n-1)实际上是对hash的每一位都进行了&操作,这种运算等价于hash % n,但是运算效率更高,为什么等价呢?下面附上证明:
抹除高位,只保留低位就相当于减去高位中所有的2^n的倍数(字丑,见谅)
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}注意看,这是我们常用的构造方法,但是这里面只设置了负载因子,并没有给容量,但是我们却能够直接使用,这是为什么呢?答案在put方法的源码之中文章来源:https://www.toymoban.com/news/detail-756762.html
public V put(K key, V value) {
// 调用putVal方法
return putVal(hash(key), key, value, false, true);
} 文章来源地址https://www.toymoban.com/news/detail-756762.html
文章来源地址https://www.toymoban.com/news/detail-756762.html
到了这里,关于数据结构之Map/Set讲解+硬核源码剖析的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!