图的存储结构——十字链表-Toy模板网

这篇具有很好参考价值的文章主要介绍了图的存储结构——十字链表。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

引入（为何存在？）

数据结构分析

十字链表的示意图：

代码实现（以有向网为例，创建十字链表）

数据结构部分：

算法实现部分：

测试部分：（以图8.14为例）

时间与空间复杂度分析分析：

引入（为何存在？）

回忆邻接矩阵与邻接表的存储结构，它们都不便于求顶点的出度与入度（对于每个顶点而言，欲求其出入度，邻接矩阵需要扫描2*n次，而邻接表只易在求解其出度，欲求入度还需重新扫面整张图）。为了解决上述两者求出入度的局限性，在此引入十字链表，它可以看成邻接表与逆邻接表的结合，方便求解顶点出入度与获取顶点的出入度边。

数据结构分析

十字链表的存储结构包含表头结点表与弧表，与邻接表类似，是一种顺序结合链式的存储结构，因此需要有两个指针域分别指向以顶点为弧尾和以顶点为弧头的弧结点。

表头结点表是一个顺序存储结构的数组，其结点数据类型如下图所示：

十字链表,数据结构与算法,C++,链表,数据结构,算法

分析：在表头结点中，顶点数据域存储与顶点有关的信息，本例指定为 char类型；指针域firstin指向以顶点为弧头的第一条弧，指针域firstout指向以顶点为弧尾的第一条弧。这也告诉我们，待会在创建弧<v1,v2>时，不仅需要处理v1的firstout,还需要处理v2的firstin。

弧结点的数据类型如下图所示：

十字链表,数据结构与算法,C++,链表,数据结构,算法

分析：弧尾结点存储该弧尾结点所在图中的位置，弧头结点同理；弧上信息指示权值等弧数据；hlink指向与该弧有相同弧头的弧结点，tlink指向与该弧有相同弧尾的弧结点。

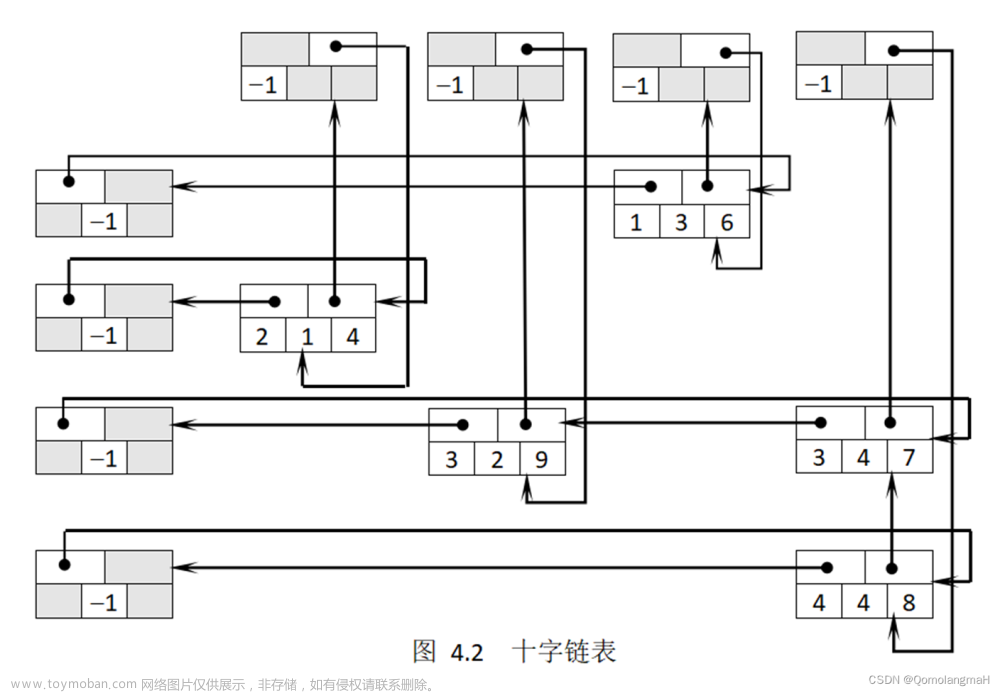
十字链表的示意图：

十字链表,数据结构与算法,C++,链表,数据结构,算法

代码实现（以有向网为例，创建十字链表）

数据结构部分：

//文件名尾：OLGraph.h
#pragma once
#include<iostream>
using namespace std;

#define Maxvex 100    //最大顶点数

//定义权值与顶点的信息类型
typedef int OtherInfo;
typedef char vexType;

//定义弧结点的数据结构
typedef struct ArcBox {
	int tvex, hvex;  //指向该弧的弧尾与弧头
	struct ArcBox* tlink, * hlink;    //指向与该弧有相同弧尾与弧头的弧结点
	OtherInfo w;  //弧上信息
}ArcBox;

//定义表头结点的数据结构
typedef struct VexNode {
	vexType data; //数据域
	struct ArcBox* firstin, * firstout;  //该顶点的第一条入度弧结点与出度弧结点
}VexNode;

//定义十字链表的数据结构
typedef struct OLGraph {
	VexNode xlist[Maxvex];  //表头结点表的最大容量为maxvex
	int vexnum, arcnum;    //顶点与弧的个数
}OLGraph;


//创建十字链表
void CreateUDNol(OLGraph& G);

算法实现部分：

注意：顶点编号从0开始

文件名为：OLGraph.cpp
#include"OLGraph.h"

void CreateUDNol(OLGraph& G)
{
	//常规操作，确定顶点数与弧数
	cout << "输入顶点个数以及弧数:>" << endl;
	cin >> G.vexnum >> G.arcnum;
	if (G.vexnum > Maxvex || G.arcnum > (G.vexnum - 1) * G.vexnum|| G.vexnum<1)
	{
		cout << "数据有误" << endl;
		return;
	}
	//将顶点数据初始化,输入顶点数据
	cout << "请输入" << G.vexnum << "个顶点的数据域:>";
	for (int i = 0;i < G.vexnum;i++)
	{
		cin >> G.xlist[i].data;
		//指针域需要初始化
		G.xlist[i].firstin = G.xlist[i].firstout = NULL;
	}
	//输入边的数据，出入度结点以及权值并连接结点
	for (int i = 0;i < G.arcnum;i++)
	{
		/*
			还有一种输入顶点数据域再找该顶点编号的输入方式，这里直接输入顶点
			编号
		*/
		cout << "请输入<v1,v2>中的顶点v1、v2编号以及该弧的权值w:>" << endl;
		//创建<v1,v2>
		int v1, v2, w;
		cin >> v1 >> v2 >> w;
		//判断合法性
		if (v1 >= G.vexnum || v2 >= G.vexnum||v2<0||v1<0||v1==v2)
		{
			i--;
			cout << "数据有误,请重新输入！" << endl;
			continue;
		}
		ArcBox* p = new ArcBox;
		p->hvex = v2;   //v2是该弧的头结点
		p->tvex = v1;   //v1是该弧的尾结点
		p->w = w;
		//连接p与其有相同出度点的弧结点
		p->tlink = G.xlist[v1].firstout;
		G.xlist[v1].firstout = p;
		//连接p与其有相同入度点的弧结点
		p->hlink = G.xlist[v2].firstin;
		G.xlist[v2].firstin = p;
	}
}

测试部分：（以图8.14为例）

输出各个顶点的出度与入度点：

//文件名：test.cpp
void test()
{
	OLGraph G;
	CreateUDNol(G);
	//输出每个顶点的出度点与入度点
	for (int i = 0;i < G.vexnum;i++)
	{
		cout << "该顶点的下标为：" << i << "  其数据域：" << G.xlist[i].data;
		cout << "  该顶点的出度弧：";
		ArcBox* p = G.xlist[i].firstout;
		while (p)
		{
			int node = p->hvex;
			cout << node << ": " << G.xlist[node].data << " ";
			p = p->tlink;
		}
		cout << "该顶点的入度弧：";
		p = G.xlist[i].firstin;
		while (p)
		{
			int node = p->tvex;
			cout << node << ": " << G.xlist[node].data << " ";
			p = p->hlink;
		}
		cout << endl;
	}
}


int main()
{
	test();
	return 0;
}

测试结果：

十字链表,数据结构与算法,C++,链表,数据结构,算法

时间与空间复杂度分析分析：

空间复杂度：由于需要存储n个顶点与e条边，故空间复杂度为：O（n+e）;

时间复杂度：就创建算法而言，时间花销主要在顶点数据与弧信息的输入，若有向网有n个顶点与e条边，那么时间复杂度为:O(n+e)；就查找顶点的出入度的算法而言，由于每个顶点与每个顶点的出入弧只需要扫描一次，故时间复杂度为O(n+e)，当图为稀疏图时，相比于邻接矩阵时间复杂度O(n^2)。但是当图为稠密图时，考虑到十字链表指针域的额外花销，邻接矩阵便有使用价值。

文章来源地址https://www.toymoban.com/news/detail-757135.html

到了这里，关于图的存储结构——十字链表的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！