参考视频：
懒猫老师-数据结构-(59)平衡二叉树【互动视频】
前置概念
（1）什么是平衡二叉树
平衡二叉树（Balanced Binary Tree）是一种特殊的二叉查找树，它的目的是保持树的高度尽量平衡，以保证查找、插入、删除等操作的时间复杂度为 O(log n)。
常见的平衡二叉树算法包括 AVL 树、红黑树、伸展树等。这些算法通过记录每个节点的平衡因子或颜色，并在必要时通过旋转或重新着色来调整树的形态，以保持树的平衡。平衡二叉树的应用非常广泛，用于实现高效的数据结构，例如字典、集合等。
（2）如何判断一棵树是否是平衡二叉树
判断一棵树是否是平衡二叉树的方法有多种，具体的方法取决于具体的平衡二叉树算法。
以 AVL 树为例，判断一棵树是否是 AVL 树的方法是：
- 定义节点的高度：对于任意一个节点，它的高度等于它的左右子树的高度的最大值加 1。
- 定义节点的平衡因子：对于任意一个节点，它的平衡因子等于它左子树的高度减去它右子树的高度。
- 判断树是否平衡：对于任意一个节点，它的平衡因子的绝对值不大于 1。如果树中的所有节点都满足平衡因子的绝对值不大于 1，那么这棵树就是一棵 AVL 树。
对于其他平衡二叉树算法，如红黑树和伸展树，判断方法也有所不同，但是基本思想都是一样的：通过检查树中每个节点的相关信息（例如颜色或平衡因子），来判断树是否平衡。
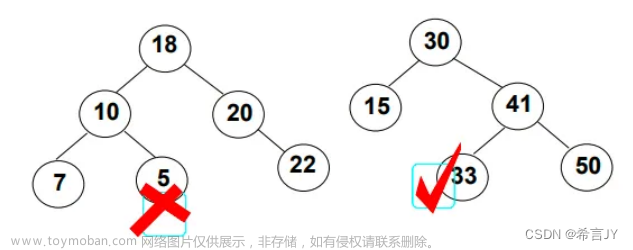
（3）最小不平衡子树
最小不平衡子树：在平衡二叉树的构造过程中，以
距离插入结点最近的、且平衡因子的绝对值大于1的结点为根的子树。
例如上图，此处4就是最小不平衡子树的根节点。
一、构造平衡二叉树的基本思想
每插入一个结点，
- 从插入结点向上计算各结点的平衡因子，如果某结点的平衡因子的绝对值大于1，则说明插入操作破坏了二叉排序树的平衡性，需要进行平衡调整；否则继续执行插入操作。
- 如果二叉排序树不平衡，则找出最小不平衡子树的根节点，根据新插入结点与最小不平衡子树根节点的关系判断调整类型。
- 根据调整类型进行相应的调整，使之成为新的平衡子树。
二、一个示例
三、平衡二叉树的调整细节
设结点A为最小不平衡子树的根结点，对该子树平衡调整有以下四种情况：
- LL型
- RR型
- LR型
- RL型
（1）LL型（顺时针 ）
插入结点X之后，这棵二叉树不平衡了。B结点的平衡因子变成1（h+1-h），A结点的平衡因子变成2（h+2-h）。这里我们称X结点为问题的发生者；A结点为问题的发现者。从问题的发现者A结点到问题的发生者要经过左子树的左子树（即LL）。
现在A发现二叉树不平衡了，就需要对二叉树进行调整。
旋转：扁担原理； 冲突：旋转优先
利用扁担原理，A结点的左右子树不平衡了：左子树“重”，右子树“轻”。那么我们把B结点往上抬，A结点往下压（进行了一个顺时针旋转），A结点变成了B结点的右子树，B结点原来的右子树调整为A结点的左子树（B结点的右子树上的所有结点一定小于A结点，所以将B原来的右子树调整为A结点的左子树是最合适的）。
举例
（2）RR型（逆时针）
（3）LR型（先逆时针再顺时针）
理解记忆：想象我们正在背一个扁担，发现左边重，但对于左边来说，左边的右边又比较重，所以这个LR型调整成平衡二叉树更为复杂。我们先需要对左边好好调整一番，规整一下（逆时针旋转），调整成LL型，让所有重量完全彻底地压到左边。接着对得到的LL型一次性向右调整（顺时针旋转）。
举例
（4）RL型（先顺时针再逆时针）
（5）四种调整类型总结
四、例题
解题过程
-
找到最小不平衡子树的根结点：5
-
判断类型：从问题的发现者开始到问题的发生者，先左后右，画圈的为RL型不平衡树。
注意：下面对画圈的部分独立操作。 -
将RL型的不平衡树进行顺时针旋转变成RR型
-
插入结点9，发现二叉树又不平衡了，找到最小不平衡子树的根结点：4
- 判断类型：RR型不平衡树
- 对RR型不平衡树进行逆时针旋转
文章来源：https://www.toymoban.com/news/detail-757142.html
文章来源地址https://www.toymoban.com/news/detail-757142.html
到了这里，关于【数据结构】二叉排序树——平衡二叉树的调整的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
