关键路径——AOE-网

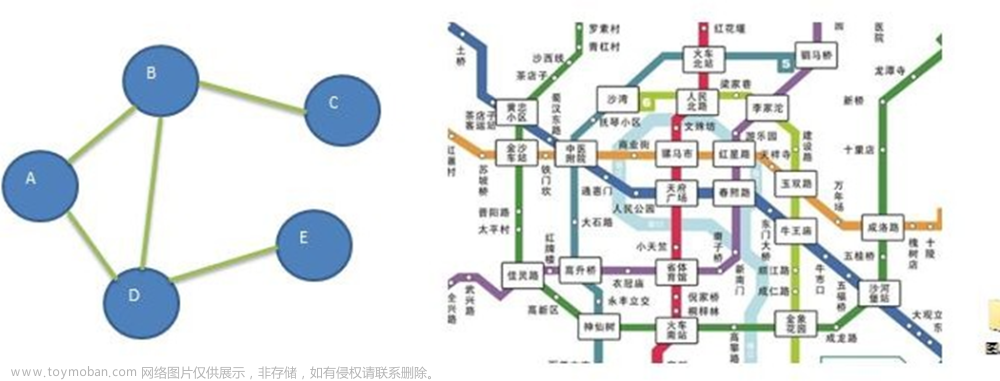
AOE-网的介绍

与AOV-网有所不同，AOE-网是以顶点存储事件，以弧<vi,vj>表示活动的带权的有向无环图，权值表示活动<vi,vj>的持续时间。一般的工程中除了子工程之间存在着先决关系外，每一项子工程或活动的完成都需要特定时间。各个子工程的完成时间参差不齐，为了统筹一个工程的人力与物力资源更好的分配于各项活动，产生了用于评估工程用时的AOE-网的关键路径算法。总之，AOE-网的关键路径算法用于评估整个工程的持续时间以及判断哪些活动是影响整个工程的关键。

注意，AOE-网的顶点所代表的事件，可以指代多个活动的开始或者结束。

如上图所示，顶点C代表的事件为活动<A,C>的结束以及活动<C,E>的开始。可见，顶点v代表以v为弧头的活动的结束，也代表着以v为弧尾的活动的开始。弧<vi,vj>暗含事件vi与vj的发生次序。

通常一个工程都有始有终，代表整个工程开始的顶点称为源点，代表整个工程结束的顶点称为汇点，，源点的入度为0，汇点的出度为0。从事件vi到事件vj所经历的时间等于从顶点vi到顶点vj所经历的路径长度。很显然，整个工程的持续时间等于从源点到汇点所经历的最长路径。在工程中的所有活动中，最早开始时间等于最迟开始时间的活动被称为“关键活动”，关键活动直接影响整个工程的持续时间，关键活动所组成的路径恰好等于最长路径，且该路径不唯一。

四个表述量

求解AOE-网的关键活动需要引入4个表述量，分别为：

（1）事件vi的最早开始时间，设为ve(i)

源点事件的最早开始时间：ve(0)=0；对于非源点事件vj而言，ve(j)=Max{ve(i)+w(i,j)}，意为非源点事件的最早开始时间等于先决事件的最早开始时间加上活动<vi,vj>的持续时间的最大值，因为该事件vj需要等待前面的所有活动完成才能开始，故取最大值。同时，汇点事件的最早开始时间ve(n-1)等于整个工程的持续时间。

（2）事件vi的最迟开始时间，设为vl(i)

汇点事件的最迟开始时间：vl(n-1)=ve(n-1); 对于非汇点事件vi而言，vl(i)=Min{vl(j)-w(i,j)},意为非汇点事件的最迟开始事件等于其直接后驱时间减去活动<vi,vj>的持续时间的最小值，为了不耽误后续的工期，故取最小值。

(3)活动<vi,vj>的最早开始时间，设为e

e=ve(i)

(4)活动<vi,vj>的最迟开始时间，设为l

l=vl(j)-w(i,j)

判断活动<vi,vj>是否为关键活动的依据：

当e==l时，说明该活动的最早开始时间等于最晚开始时间，期间没有时间余额，需要亟待解决。同理，如果l>e,说明该事件即时稍许片刻开始也不会影响工期。

关键路径算法的求解与实现过程

1. 对AOE-网中的各个事件进行拓扑排序，将排序结果存放在int topo[n]数组中；

2. 定义数组int ve[n]存放事件vi的最早开始时间，由于求解过程满足递推公式，可以按照拓扑次序依次求解出ve(i);

3. 定义数组int vl[n]存放事件vj的最晚开始事件，首先vl[n]全部赋值为ve[n-1],由于求解过程满足递推公司，可以按照逆拓扑次序求解出vl(j);

4. 从邻接表的顶点下标i=0开始，依次判断活动<vi,vj>的最早开始时间与最晚开始时间的大小关系，若e==l,则输出活动<vi,vj>，表示其为关键活动。所有从源点到汇点相连的所有关键活动组成的路径即为关键路径，同时关键路径不唯一。

关键路径算法

1. 利用邻接表存储AOE-网，对AOE-网做拓扑排序，排序结果存放在int topo[n]数组中；

2. 初始化一个int ve[n]数组，依次选取拓扑序列中的数值：int i = topo[k],遍历下标为i的顶点的所有边，int j = p->adjvex,判断：if(ve(j)<ve(i)+w(i,j)) ve(j)=ve(i)+w(i,j);

3. 初始化一个int vl[n]数组，依次选取逆拓扑序列中的数值:int i =topo[k],遍历下标为k的顶点的所有边，int j = p->adjvex,判断if(vl(i)>vl(j)-w(i,j)) vl(i)=vl(j)-w(i,j)；

4. 从邻接表下标为0的顶点开始，依次选取该顶点i的所有邻接点int j = adjvex,若ve(i)=vl(j)-w(i,j),则输出该活动<vi,vj>，直到遍历完所有的顶点。

代码实现

//文件名为：ALGraph.h
#pragma once
#include<iostream>
#include<string>
using namespace std;

#define Maxvex 100

typedef char VexType;   //顶点信息      
typedef int OtherInfo;  //权值信息

//边表的存储结构
typedef struct ArcNode {
    int adjvex;                    //邻接顶点
    OtherInfo w;
    struct ArcNode* nextarc;     //下一个结点
}ArcNode;

//表头结点表的存储结构
typedef struct {
    VexType data;   //顶点vex数据域
    ArcNode* fisrtarc;
}vNode, Adjlist[Maxvex];

//图的存储结构
typedef struct ALGraph {
    Adjlist  vertices;    //定义表头结点表数组
    int vexnum, arcnum;   //顶点数以及边(弧)的数目
}ALGraph;

//创建一个邻接表
void CreateUDN(ALGraph& G);
//删除该邻接表
void Del(ALGraph& G);

//文件名为:ALGraph.cpp
#include"ALGraph.h"

int Findvex(const VexType& v, ALGraph& G)
{
    for (int i = 0;i < G.vexnum;i++)
    {
        if (G.vertices[i].data == v)
            return i;
    }
}


void CreateUDN(ALGraph& G)
{
    //首先需要输入表的顶点vexnum与边数arcnum
    cout << "请输入顶点数以及弧数:>" << endl;
    cin >> G.vexnum >> G.arcnum;
    if (G.vexnum > Maxvex || G.arcnum > (G.vexnum - 1) * G.vexnum)
    {
        cout << "fail Create" << endl;
        return;
    }
    cout << "请输入各个顶点所代表的活动:>" << endl;
    for (int i = 0;i < G.vexnum;i++)
    {
        cin >> G.vertices[i].data;
        G.vertices[i].fisrtarc = NULL;
    }
    //连接各个顶点，输入边的权值以及边的指向顶点信息
    cout << "输入弧<v1,v2>的顶点v1,v2以及权值:>" << endl;
    for (int i = 0;i < G.arcnum;i++)
    {
        OtherInfo w;
        VexType v1, v2;
        cin >> v1 >> v2;
        cin >> w;
        //寻找顶点v1的下标
        int V1 = Findvex(v1, G);
        //寻找顶点v1的下标
        int V2 = Findvex(v2, G);
        if (V1 >= Maxvex || V2 >= Maxvex)
        {
            i--;
            cout << "数据输入有误，请重新输入！" << endl;
            continue;
        }
        //连接v1到v2的边，并且完善该边的信息
        ArcNode* p1 = new ArcNode;
        p1->adjvex = V2;
        p1->w = w;
        //注意编号从0开始
        p1->nextarc = G.vertices[V1].fisrtarc;
        G.vertices[V1].fisrtarc = p1;
    }
}

void DelAlg(ArcNode*& p)
{
    if (p == NULL)
    {
        return;
    }
    DelAlg(p->nextarc);
    delete p;
    //cout << "删除成功!" << endl;
    p = NULL;
}

//删除该邻接表
void Del(ALGraph& G)
{
    for (int i = 0;i < G.vexnum;i++)
    {
        DelAlg(G.vertices[i].fisrtarc);
    }
}

//文件名：CriticalPath.cpp
#include"ALGraph.h"
#include<stack>


/*
    为此，你需要先获取AOE网的拓扑排序，即vl,ve的递推顺序
*/

//GetInDegree
void GetInDegree(const ALGraph& G, int* Indegree)
{
    //扫描e条边即可
    for (int i = 0;i < G.vexnum;i++)
    {
        ArcNode* p = G.vertices[i].fisrtarc;
        while (p)
        {
            //顶点vi的邻接点adject的入度加一
            Indegree[p->adjvex]++;
            p = p->nextarc;
        }
    }
}

//TopologicalSort
void TopologicalSort(const ALGraph& G, int* topo)
{
    //借助Indegree[maxvex]
    int Indegree[Maxvex] = { 0 };
    //获取各个顶点的入度
    GetInDegree(G, Indegree);

    //先让入度为0的顶点入栈
    stack<int> S;
    
    for (int i = 0;i < G.vexnum;i++)
    {
        if (Indegree[i] == 0)
            S.push(i);
    }
    //记录拓扑排序中的元素序号
    int m = 0;

    while (!S.empty())
    {
        //当栈不为空时
        //顶点元素出栈
        int k = S.top();
        S.pop();
        topo[m] = k;
        m++;
        //顶点vk对应邻接点的入度减少1
        ArcNode* p = G.vertices[k].fisrtarc;
        while (p)
        {
            Indegree[p->adjvex]--;
            if (Indegree[p->adjvex] == 0)
            {
                S.push(p->adjvex);
            }
            p = p->nextarc;
        }
    }
    if (m == G.vexnum)
    {
        cout << "Successfully" << endl;
    }
    else
    {
        cout << "Fail" << endl;
    }
}

void CriticalPath(const ALGraph& G)
{
    //拓扑排序辅助V,E的递推
    int topo[Maxvex] = { 0 };
    TopologicalSort(G, topo);
    //记录顶点个数
    int n = G.vexnum;    
    //记录事件发生的最早时间
    //扫描e条弧<i,j>,判断j当前的最早发生时间是否小于e(i)+w(i,j)
    int ve[Maxvex] = { 0 };

    /*--------按拓扑次序获取事件的最早发生时间------------ - */
    for (int k = 0;k < n;k++)
    {
        //若弧<i,j>存在，则i<j
        int i = topo[k];
        ArcNode* p = G.vertices[i].fisrtarc;
        while (p)
        {
            int j = p->adjvex;
            if (ve[j] < ve[i] + p->w)
            {
                ve[j] = ve[i] + p->w;
            }
            p = p->nextarc;
        }
    }

    //记录事件发生的最迟发生时间
    int vl[Maxvex] = { 0 };
    //初始化
    for (int i = 0;i < n;i++)
    {
        //初始值等于该工程的结束时间，也就是最后一件事的最早发生时间
        vl[i] = ve[n - 1];
    }

    /*---------按拓扑逆序获取事件的最迟发生时间-------*/
    for (int k = n - 1;k >= 0;k--)
    {
        //按拓扑逆序获取每一件事情的最迟发生时间
        //判断在弧<i,j>中，vl(i)是否大于vl(i)-w(i,j)
        int i = topo[k];
        ArcNode* p = G.vertices[i].fisrtarc;
        while (p)
        {
            int j = p->adjvex;
            if (vl[i] > vl[j] - p->w)
            {
                vl[i] = vl[j] - p->w;
            }
            p = p->nextarc;
        }
    }

    /*-----输出关键活动-----*/
    //在弧<vi,vj>已知的情况下，可以获取活动<vi,vj>的最早发生时间e=ve(i)
    //以及它的最晚发生时间l=vl(j)-w(i,j)

    cout << "该工程的关键活动如下:>" << endl;
    for (int i = 0;i < n;i++)
    {
        ArcNode* p = G.vertices[i].fisrtarc;
        while (p)
        {
            int j = p->adjvex;
            //如果该活动的最早发生时间与最迟发生时间相等，那么其为关键活动
            if (ve[i] == vl[j] - p->w)
            {
                cout << "<" << G.vertices[i].data 
                    << "," << G.vertices[j].data << ">" << endl;
            }
            p = p->nextarc;
        }
    }
}

int main()
{
    ALGraph G;
    CreateUDN(G);
    CriticalPath(G);
    Del(G);
    return 0;
}

测试结果如下：

如图所示，关键路径并不唯一，活动<A,B> <B,E><E,F><F,I>所组成的ABEFI路径是关键路径，活动<A,B> <B,E><E,G><G,I>所组成的ABEGI路径也是关键路径。如果在工程中存在多条关键路径，则若想减少工程总时间，就需要同时减少多条关键路径的长度。同时由于网中的所有活动都是相互关联的，一旦每个活动的持续时间被修改，就应该重新计算网的关键路劲。

算法分析

在求解事件的最早与最迟开始时间与求解活动的最早与最迟开始时间都需要扫描网的n个顶点与e条边，故时间复杂度为O(n+e)；同时，由于借助了ve,vl数组，故空间复杂度为O(n).文章来源地址https://www.toymoban.com/news/detail-757266.html