一、实验项目要求
1.输入一个表达式(表达式中的数均小于10的正整数),利用二叉树来表示该表达式,创建表达式数,然后利用二叉树的遍历操作求表达式的值。
2.输入要求:多组数据,每组数据1行,为一个表达式,表达式以“=”结尾。当输入只有一个“=”时,输入结束。
3.输出要求:每组数据输出一行,为表达式的值。
4.输入样例:2*(2+5)=
1+2=
=
输出样例:
14
3
二、理论分析
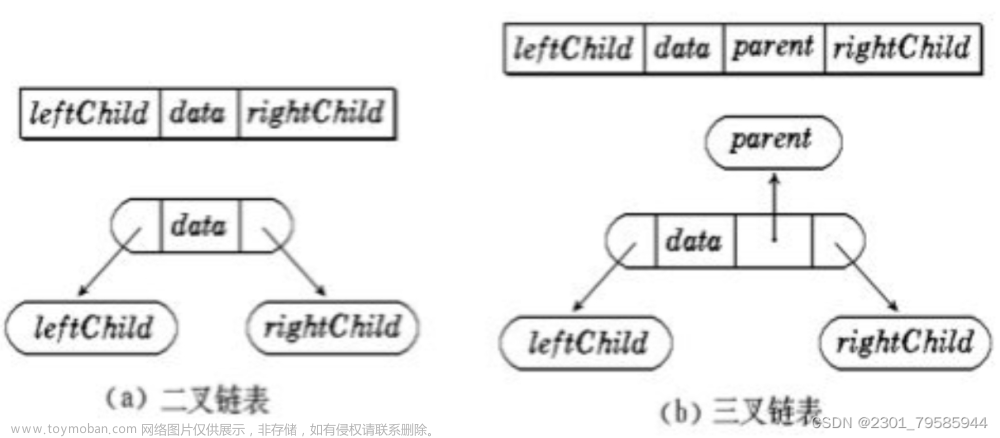
第一,输入表达式,创建一个基于二叉链表表示的表达式树,里面包含树节点定义。定义了树的节点和节点指针。
第二,对表达式树进行后序遍历,得到表达式的值。
第三,针对算术表达式,都可用二叉树来表示。表达式对应的二叉树创建后,利用二叉树的遍历等操作,很容易实现表达式的求值运算。由于创建的表达式树需要准确的表达运算次序,因此在扫描表达式创建表达式树的过程中,当遇到运算符时不能直接创建结点,而应将其与前面的运算符进行优先级比较,根据比较的结果再进行处理。
第四,根据表达式树与表达式对应关系的递归定义,每两个操作数和一个运算符就可以建立一棵表达式二叉树,而该二叉树又可以作为另一个运算符结点的一棵子树。可以另外借助一个表达式树栈,来暂存已建立好的表达式树的根结点,以便其作为另一个运算符结点的子树而被引用。
三、实现方法
#include<iostream>
#include <cstdio>
using namespace std;
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define STACK_INIT_SIZE 100
#define STACKINCREMENT 10
typedef int Status;
typedef char TElemType;
typedef int ElemType;
typedef struct BiNode
{
TElemType data;
struct BiNode* lchild;
struct BiNode* rchild;
}BiNode, * BiTree;
typedef BiTree SBElemType;
int preorderTraverse(BiTree T)
{
if (T == NULL)
return 0;
else
{
cout<<T->data;
preorderTraverse(T->lchild);
preorderTraverse(T->rchild);
}
}
int InorderTraverse(BiTree T)
{
if (T == NULL)
return 0;
else
{
InorderTraverse(T->lchild);
cout<<T->data;
InorderTraverse(T->rchild);
}
}
int PostorderTraverse(BiTree T)
{
if (T == NULL)
return 0;
else
{
PostorderTraverse(T->lchild);
PostorderTraverse(T->rchild);
cout<<T->data;
}
}
typedef struct
{
TElemType* base;
TElemType* top;
int stacksize;
}SqStack;
Status InitStack(SqStack* S)
{
S->base = (TElemType*)malloc(STACK_INIT_SIZE * sizeof(TElemType));
if (!S->base)
{
cout<<"内存分配失败!\n";
exit(0);
}
S->top = S->base;
S->stacksize = STACK_INIT_SIZE;
return OK;
}
Status GetTop(SqStack* S, TElemType* e)
{
if (S->top == S->base)
return ERROR;
*e = *(S->top - 1);
return OK;
}
Status Push(SqStack* S, TElemType e)
{
if (S->top - S->base >= STACK_INIT_SIZE)
{
S->base = (TElemType*)realloc(S->base, (S->stacksize + STACKINCREMENT) * sizeof(TElemType));
if (!S->base)
{
cout<<"内存分配失败!\n";
exit(OVERFLOW);
}
S->top = S->base + S->stacksize;
S->stacksize += STACKINCREMENT;
}
*S->top++ = e;
return OK;
}
Status Pop(SqStack* S, TElemType* e)
{
if (S->top == S->base)
return ERROR;
*e = *--S->top;
return OK;
}
typedef struct {
SBElemType* base;
SBElemType* top;
int stacksize;
} SqStack_BiTree;
void SqStack_BiTree_InitStack(SqStack_BiTree& S)
{
if (!(S.base = (SBElemType*)malloc(STACK_INIT_SIZE
* sizeof(SBElemType))))
exit(0);
S.top = S.base;
S.stacksize = STACK_INIT_SIZE;
}
void SqStack_BiTree_DestroyStack(SqStack_BiTree& S)
{
free(S.base);
S.base = NULL;
S.top = NULL;
S.stacksize = 0;
}
void SqStack_BiTree_Push(SqStack_BiTree& S, SBElemType e)
{
if (S.top - S.base >= S.stacksize)
{
S.base = (SBElemType*)realloc(S.base, (S.stacksize
+ STACKINCREMENT) * sizeof(SBElemType));
if (!S.base)
exit(OVERFLOW);
S.top = S.base + S.stacksize;
S.stacksize += STACKINCREMENT;
}
*(S.top)++ = e;
}
Status SqStack_BiTree_Pop(SqStack_BiTree& S, SBElemType& e)
{
if (S.top == S.base)
{
return ERROR;
}
e = *--S.top;;
return OK;
}
Status SqStack_BiTree_GetTop(SqStack_BiTree S, SBElemType& e)
{
if (S.top > S.base) {
e = *(S.top - 1);
return OK;
}
else
{
return ERROR;
}
}
char Precede(char t1, char t2)
{
int i, j;
char pre[7][7] = {
{'>','>','<','<','<','>','>'},
{'>','>','<','<','<','>','>'},
{'>','>','>','>','<','>','>'},
{'>','>','>','>','<','>','>'},
{'<','<','<','<','<','=','0'},
{'>','>','>','>','0','>','>'},
{'<','<','<','<','<','0','='} };
switch (t1) {
case '+': i = 0; break;
case '-': i = 1; break;
case '*': i = 2; break;
case '/': i = 3; break;
case '(': i = 4; break;
case ')': i = 5; break;
case '=': i = 6; break;
}
switch (t2) {
case '+': j = 0; break;
case '-': j = 1; break;
case '*': j = 2; break;
case '/': j = 3; break;
case '(': j = 4; break;
case ')': j = 5; break;
case '=': j = 6; break;
}
return pre[i][j];
}
Status In(TElemType c)
{
switch (c)
{
case '+':
case '-':
case '*':
case '/':
case '(':
case ')':
case '=':
return TRUE;
default:
return FALSE;
}
}
ElemType Operate(ElemType a, TElemType theta, ElemType b)
{
TElemType c;
switch (theta)
{
case '+':
c = a + b;
break;
case '-':
c = a - b;
break;
case '*':
c = a * b;
break;
case '/':
c = a / b;
break;
}
return c;
}
void EvaluateExpression(BiTree& root, char* str)
{
SqStack OPTR;
InitStack(&OPTR);
SqStack_BiTree EXPT;
SqStack_BiTree_InitStack(EXPT);
char ch, x, theta;
BiTree a, b;
int i = 0;
Push(&OPTR, '=');
ch = str[i++];
GetTop(&OPTR, &x);
while (ch != '=' || x != '=')
{
if (In(ch))
{
switch (Precede(x, ch))
{
case '<':
Push(&OPTR, ch);
ch = str[i++];
break;
case '=':
Pop(&OPTR, &x);
ch = str[i++];
break;
case '>':
Pop(&OPTR, &theta);
BiTree TEMP;
TEMP = (BiNode*)malloc(sizeof(BiNode));
if (!TEMP)
exit(-1);
TEMP->data = theta;
SqStack_BiTree_Pop(EXPT, b);
SqStack_BiTree_Pop(EXPT, a);
TEMP->lchild = a;
TEMP->rchild = b;
SqStack_BiTree_Push(EXPT, TEMP);
root = TEMP;
break;
}
}
if (ch >= '0' && ch <= '9')
{
BiTree Temp;
Temp = (BiNode*)malloc(sizeof(BiNode));
if (!Temp)
exit(-1);
Temp->data = ch;
Temp->lchild = NULL;
Temp->rchild = NULL;
SqStack_BiTree_Push(EXPT, Temp);
ch = ch = str[i++];;
}
GetTop(&OPTR, &x);
}
}
int calculate_BiTree(BiTree& T)
{
int lvalue;
int rvalue;
char theta;
if (T == NULL) return 0;
if (T != NULL)
{
if (T->lchild == NULL && T->lchild == NULL)
return T->data - '0';
else
{
lvalue = calculate_BiTree(T->lchild);
rvalue = calculate_BiTree(T->rchild);
theta = T->data;
return Operate(lvalue, theta, rvalue);
}
}
}
int main()
{
BiTree T;
char str[1000];
int result[100] = { 0 };
int number = 0;
do
{
cout << "输入表达式:";
cin.getline(str,30);
EvaluateExpression(T, str);
result[number] = calculate_BiTree(T);
number++;
} while (strcmp(str, "=") != 0);
for (int j = 0; j < number - 1; j++)
{
cout << endl;
cout<<"表达式运算结果: " << result[j] << endl;
}
}
三、实验结果分析

1.本实验遇到的问题与解决的方法
通过这次实验我学到了对二叉树的遍历和二叉树的创建等等,而且当遇到运算符时不能直接创建结点,而应将其与前面的运算符进行优先级比。
2.对设计及调试过程的心得体会文章来源:https://www.toymoban.com/news/detail-757286.html
从这次实验,我知道了要学好数据结构必须得亲自动手去编写算法,经过本次实验我才发现自己是多么的单纯,在编写过程中还是出了许多问题。以后一定要加强动手编写,不能因为困难而放弃学习。文章来源地址https://www.toymoban.com/news/detail-757286.html
到了这里,关于数据结构——基于二叉树的表达式求值算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!