第四章，向量组，2-矩阵等价与向量组等价的关系-Toy模板网

这篇具有很好参考价值的文章主要介绍了第四章，向量组，2-矩阵等价与向量组等价的关系。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

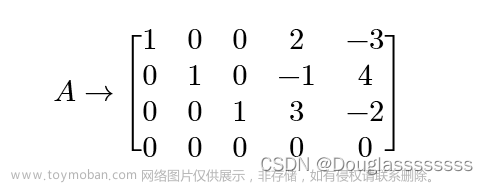
玩转线性代数(23)线性组合与线性表示的应用的笔记，相关证明以及例子见原文

矩阵乘法与线性表示

设有 $A_{m*n}B_{n*l}=C_{m*l}$ ，那么A、B矩阵的行、列向量组与C的行、列向量组之间有什么关系呢？
先看C的行向量组， $C = A B$ ，根据初等变换的知识，A在B左边，说明是对B进行的行变换（此时的行变换不一定是初等行变换，也不一定是可逆的），将B的行变成了C的行，故C的行向量组可以由B的行向量组来线性表示，如下：
$\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{pmatrix} \begin{pmatrix} b_1^T\\ b_2^T\\ \vdots \\ b_n^T\\ \end{pmatrix}=\begin{pmatrix} c_1^T\\ c_2^T\\ \vdots \\ c_m^T\\ \end{pmatrix}$
同理，C的列向量组可由A的列向量组线性表示
$\begin{pmatrix} c_1 & c_2 & \cdots & c_l \end{pmatrix}= \begin{pmatrix} a_1 & a_2 & \cdots & a_n \end{pmatrix} \begin{pmatrix} b_{11} & b_{12} & \cdots & b_{1n} \\ b_{21} & b_{22} & \cdots & b_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ b_{n1} & b_{n2} & \cdots & b_{nl} \\ \end{pmatrix}$

矩阵等价与向量组等价

矩阵等价是两个矩阵可经过初等变换来相互转化；两个向量组等价是指它们可以相互线性表示。两个向量组等价的判断条件也已经清楚，就是 $R (A) = R (B) = R (A, B)$
矩阵等价有行等价、列等价和等价有一种形式，如何判断两个矩阵等价？首先矩阵是同型矩阵，其次矩阵A与B的秩相等。因为若 $R (A) = R (B)$ ，则A与B的标准形是相同的，即
$A\sim F=\begin{pmatrix} E_r & 0\\ 0 & 0 \end{pmatrix}$ ,同时 $B\sim F=\begin{pmatrix} E_r & 0\\ 0 & 0 \end{pmatrix}$
根据等价矩阵的传递性知， $A\sim B$ 。
由此可知，对两个向量组 $A:a_1,a_2,\cdots,a_m, B:b_1,b_2,\cdots,b_l$ 和两个矩阵 $A=(a_1,a_2,\cdots,a_m), B:(b_1,b_2,\cdots,b_l)$ ，向量组A与B等价 $\Rightarrow$ 矩阵A与B等价，反之不成立。

若矩阵A与B等价，可以推出的结论：
（1）若 $A^r_{\sim}B$ ，则存在可逆矩阵P，使PA=B，即B=PA，所以B的行向量组可由A的行向量组线性表示，同时有 $A=P^{-1}B$ ，所以A的行向量组也可以由B的行向量组线性表示，说明A与B的行向量组等价；
（2）若 $A^c_{\sim}B$ ，A与B的列向量组是等价的。

其实线性表示与线性组合这些概念也可以用到方程组上．对方程组A的各个方程作线性运算所得到的一个方程就称为方程组A的一个线性组合；若其中一个方程可以写成其它方程的线性组合，则称该方程可由其它方程线性表示，若方程组B的每个方程都可由方程组A的线性表示，就称方程组B能由方程组A线性表示，这时方程组A 的解一定是方程组B的解；若方程组A与方程组B能相互线性表示，就称这两个方程组等价，等价的方程组一定同解

为什么方程组B能由方程组A线性表示，方程组A 的解一定是方程组B的解？
理解：方程组B能由方程组A线性表示，即若 $x\in A$ 一定有 $x\in B$ ，所以A的解都是B的解，B的解集合范围大。文章来源地址https://www.toymoban.com/news/detail-757317.html