* * * * * * The Machine Learning Noting Series * * * * * *
决策树(Decision Tree)是机器学习的核心算法之一,在较小训练样本或有限计算资源下仍有较好表现,它包括分类树和回归树,是目前应用最广泛的分类预测和回归预测方法。
导航
0 引言
1 决策树的概念
分类树
回归树
2 决策树的生长
分类算法
分类过程
3 决策树的剪枝
剪枝算法
剪枝过程
4 python代码实现——实例应用
- - - - - - - - - - -
0 引言
考虑这样一个药品筛选问题,大批患有同种疾病的不同病人,服用5种候选药后取得同样的效果,现有每个病人服药前的几项生理指标数据,要通过这些数据来得到选药的建议,即要根据任何一个此类病人的生理指标来得到最合适药物的建议,这就可以使用决策树方法,建立以药物为输出变量,以生理指标为输入变量的多分类预测模型。此案例在文章最后给出。
1 决策树概念
分类树
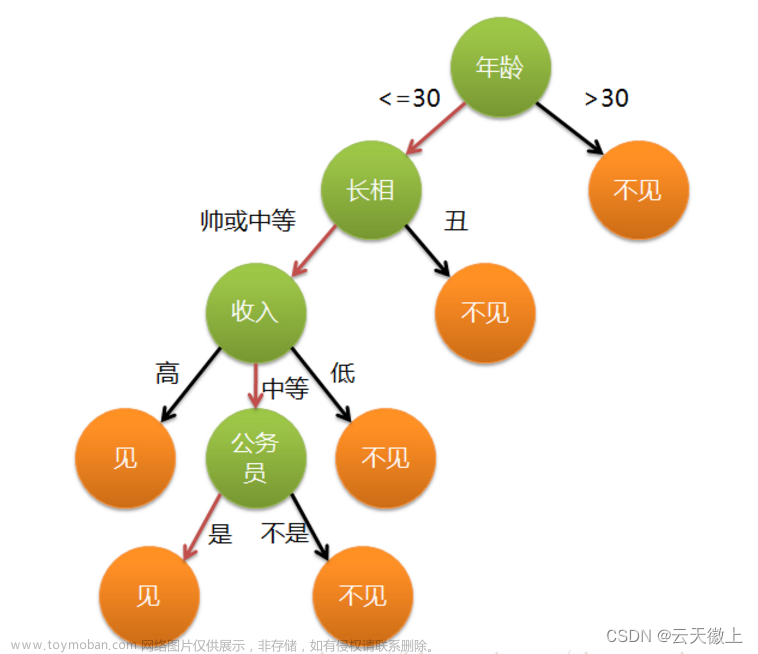
以一个例子说明决策树概念。右侧图为一个典型的树深度等于4的决策树。树深度是树根到树叶的最大层数,通常为决策树模型复杂度的度量。每个椭圆为树的节点,有向箭头将各层节点连在一起构成树的分支,一个分支的上下节点分别成为父、子节点,每个父节点下均仅有2个子节点的称为2叉树,2个以上节点的为多叉树。根节点包含所有样本,按照某种分类算法分出的子节点分别包含父节点的部分样本,在末端且没有子节点的称为叶节点。
左侧图为右侧决策树的分类边界示意。右侧决策树根节点按 X2<5 规则生成第一层的左右两个子节点,分别对应左图水平线 X2=5 分割形成的上下两个区域,后面的分割依次类推。

回归树
回归树本质上也是对 p+1 (p个输入变量)维空间的划分,下图展示了两个输入变量 X1 和 X2 以及一个输出变量 Y 的回归平面。左图为使用线性回归模型 所得的回归平面,右图为回归树的回归面。右图回归面按照一定的规则进行划分,例如最高面是按照规则 X1<-2.9和X2>3.4 划分的。图中深色观察测点的输出变量实际值大于预测值,样本观测点位于回归面上方,浅色点相反,可见回归树复杂度高,能有效分析输入和输出变量间的非线性关系,解决非线性回归问题。

分类树空间划分的先后顺序和位置,每次划分应使分出的两个区域所包含的观测点的输出变量取值差异及异质性尽量低,即两区域的离差平方(或MES)和应为最小,公式为:(其中R为划分区域,为输出变量预测值)
2 决策树的生长
分类回归树CART(Classification and Regression Tree)为二叉树,使用贪心算法,自顶向下的递归二分策略实现区域划分。其他算法包括ID3和C4.5这里不做介绍。
分类算法
分类由节点异质性(也称为纯洁度(Purity))决定,异质性越小表明子节点观测值类别相同程度越高,分类越合适。
⚫ CART分类树使用基尼系数(Gini)(或者熵[参考点击这里] )度量节点异质性,节点 t 的基尼系数为:
其中 K 为输出变量的类别数, 是节点 t 中输出变量取第 k 类的概率。可见当节点 t 中输出变量均取同一类值即没有异质性时,基尼系数取最小值为0;当输出变量异质性最大时基尼系数取到最大值 1-1/k .
⚫ CART回归树使用方差度量异质性,节点 t 方差为:
其中,y(t) 为节点 t 中样本观测 X 的输出变量值, 为节点 t 中输出变量的均值。
分类过程
⚫ 分类树节点的划分应使左()右()子节点的基尼系数均取到最小值,但通常无法做到,因此只需取两者的加权平均数最小即可,权重为左右节点各自的样本量占比。可见,从父节点到子节点,输出变量的异质性下降为:
“最佳”分组变量和组限应使取最大值。同理,若使用熵而非基尼系数,则使用熵替代上式中的 :
“最佳”分组同样需使上式达到最大值。需要说明的是,熵取最小值0代表节 t 无异质性,最大值取到 . 上式中的即为信息增益。
⚫ 回归树分类过程和分类树类似,只是异质性度量使用节点方差代替基尼系数。回归树异质性下降为:
“最佳”分组同样需使上式达到最大值。
3 决策树的剪枝
剪枝算法
CART的后剪枝采用最小代价复杂度剪枝法(Minimal Cost Complexity Pruning,MCCP),剪枝的目的是解决模型的过拟合,以得到测试误差最小的树,或者说,达到复杂度和测试误差的平衡。
可以使用叶节点个数来测度决策树的复杂度,将误差看成树的“测试代价”,那么树 T 的代价复杂度定义为:
其中,为树T的叶节点个数,α为复杂度参数(Complexity Parameter,CP参数),R(T)为测试误差:对于分类树使用判错率计算;对于回归树使用均方误差或者离差平方和计算,即此时:
一般希望测试误差R(T)和模型复杂度均较低,但两者其实是此高彼低的关系,因此只要两者之和即代价复杂度较小即可。
此外,树T代价复杂度是α的函数,α=0时表示不考虑复杂度的影响,基于代价复杂度最小是最优树的原则,此时的最优树为叶节点最多的树。显然最优树与CP参数α有关,因此可以通过调整α的取值得到一系列当前最优树,而真正的最优树就在其中。
剪枝过程
在从叶节点逐渐向根节点方向剪枝的过程中,需要判断先剪哪一只,是否需要剪枝的问题。即在判断是否应剪掉中间节点{t}下的子树时,应计算两者的代价复杂度,其中中间节点的代价复杂度通常被视为剪掉其所有子树后的代价复杂度(此时仅有一个叶节点):
中间节点的子树的代价复杂度为:
其中为左右两个子节点测试误差的加权均值,权重为各自样本量占比。
基于代价复杂度最小原则,若,即时,则应剪掉子树,因为它对降低测试误差贡献很小。
CART后剪枝主要分为两个阶段


4 python代码实现——实例应用
继续引言中的例子,先说明结果,python代码放在最后。

左图可以得出,树深度达到4时两个误差均达到最小,因此最有树深度为4,右图可以看出,影响药物效果的生理指标中,最重要因素为Na/K,性别没有影响。


左图表明模型整体预测正确率为99%,对药物B的查准率较低,但整体查准率P和查全率R均达99%,说明模型分类预测性能理想。右图为此案例的决策树,从前4行可以看出,当生理指标4≤14.83,指标2小于等于0.5以及指标0小于等于49.5时,推荐使用药物A,其余类推。
本案例python代码(来自参考文献,数据可向我索要)
# 导入包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import warnings
warnings.filterwarnings(action = 'ignore')
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei'] #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
import sklearn.linear_model as LM
from sklearn.metrics import classification_report
from sklearn.model_selection import cross_val_score,train_test_split
from sklearn.datasets import make_regression
from sklearn import tree
from sklearn.preprocessing import LabelEncoder
# 数据详情
data=pd.read_csv('药物研究.txt')
le = LabelEncoder()
le.fit(data["Sex"])
data["SexC"]=le.transform(data["Sex"])
data["BPC"]=le.fit(data["BP"]).transform(data["BP"])
data["CholesterolC"]=le.fit(data["Cholesterol"]).transform(data["Cholesterol"])
data["Na/K"]=data["Na"]/data["K"]
data.head()# 生成决策树
X=data[['Age','SexC','BPC','CholesterolC','Na/K']]
Y=data['Drug']
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,train_size=0.70, random_state=123)
trainErr=[]
testErr=[]
K=np.arange(2,10)
for k in K:
modelDTC = tree.DecisionTreeClassifier(max_depth=k,random_state=123)
modelDTC.fit(X_train,Y_train)
trainErr.append(1-modelDTC.score(X_train,Y_train))
testErr.append(1-modelDTC.score(X_test,Y_test))
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(12,4))
axes[0].grid(True, linestyle='-.')
axes[0].plot(np.arange(2,10),trainErr,label="训练误差",marker='o',linestyle='-')
axes[0].plot(np.arange(2,10),testErr,label="测试误差",marker='o',linestyle='-.')
axes[0].set_xlabel("树深度")
axes[0].set_ylabel("误差")
axes[0].set_title('树深度和误差')
axes[0].legend()
bestK=K[testErr.index(np.min(testErr))]
modelDTC = tree.DecisionTreeClassifier(max_depth=bestK,random_state=123)
modelDTC.fit(X_train,Y_train)
axes[1].bar(np.arange(5),modelDTC.feature_importances_)
axes[1].set_title('输入变量的重要性')
axes[1].set_xlabel('输入变量')
axes[1].set_xticks(np.arange(5))
axes[1].set_xticklabels(['年龄','性别','血压','胆固醇','Na/K'])
plt.show()
# 打印决策树
print("模型的评价:\n",classification_report(Y,modelDTC.predict(X)))
print(tree.export_text(modelDTC))参考文献
《Python机器学习 数据建模与分析》,薛薇 等/著文章来源:https://www.toymoban.com/news/detail-758055.html
《机器学习与Pytnon实践》,黄勉 编著文章来源地址https://www.toymoban.com/news/detail-758055.html
到了这里,关于决策树的原理、方法以及python实现——机器学习笔记的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!