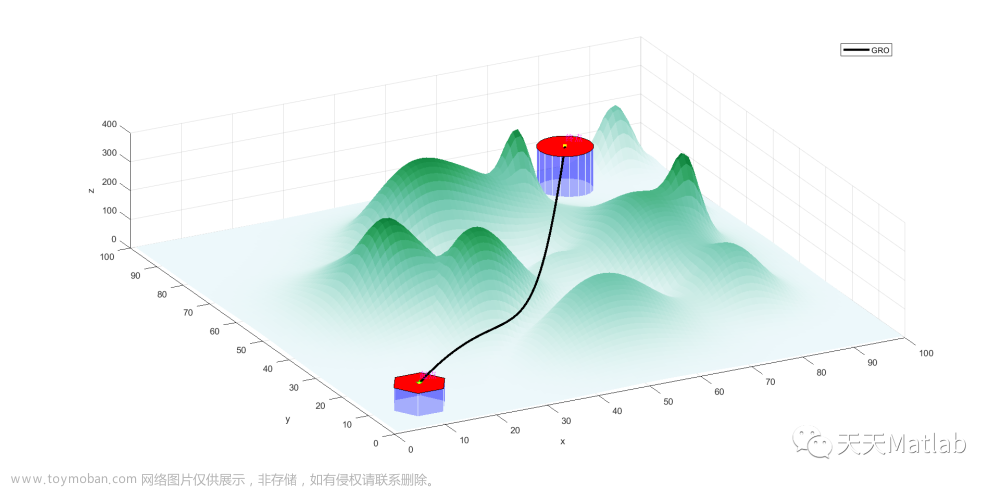
⛄一、粒子群算法无人机群威胁环境下多目标路径优化搜索探测
1 粒子群算法
粒子群算法是智能算法领域中除蚁群算法、鱼群算法又一个智能群体算法。
PSO算法首先在可行解空间中初始化一群粒子,每个粒子都代表极值优化问题的一个潜在最优解。粒子在解空间中运动,通过跟踪个体极值Pbest和群体极值Gbest更新个体位置。
粒子每更新一次位置,就计算一次适应度值,并且通过比较新粒子的适应度值和个体极值、群体极值的适应度值更新个体极值Pbest和群体极值Gbest位置。
在每一次迭代过程中,粒子通过个体极值和群体极值更新自身的速度和位置,每个粒子在D维空间的速度和位置状态可表示为
2 粒子群算法步骤
粒子群算法是一种基于群体智能的优化算法,其步骤如下:
(1)初始化粒子群:随机生成一定数量的粒子,并为每个粒子随机分配一个位置和速度。
(2)计算适应度函数:根据问题的具体情况,计算每个粒子的适应度函数值。
(3)更新粒子速度和位置:根据当前位置和速度,以及全局(4)最优位置和个体最优位置,更新每个粒子的速度和位置。
(5)更新全局最优位置和个体最优位置:根据当前适应度函数值,更新全局最优位置和个体最优位置。
(6)判断终止条件:如果满足终止条件,则输出最优解;否则返回第3步。
3 多目标粒子群算法求解多无人机多任务路分配及路径规划(最短路程+最短时间)问题
多目标粒子群算法(MOPSO)是一种用于解决多目标优化问题的算法。在多无人机多任务路分配及路径规划问题中,我们需要同时考虑最短路程和最短时间两个目标。MOPSO算法通过维护一个粒子群体,每个粒子代表一个解决方案,并通过不断地更新粒子的速度和位置来搜索最优解。在每次更新后,通过对所有粒子进行非支配排序和拥挤度距离计算,筛选出一组最优解,即帕累托前沿。这些解可以提供给决策者进行选择,以达到最优的路分配方案和路径规划方案。
下面是MOPSO算法求解多无人机多任务路分配及路径规划的步骤:
(1)初始化粒子群体,包括粒子的位置和速度。
(2)计算每个粒子的适应度值,即路分配方案和路径规划方案的目标函数值。
(3)对所有粒子进行非支配排序,得到帕累托前沿。
(4)计算每个粒子的拥挤度距离,用于保证帕累托前沿的多样性。
(5)根据粒子的适应度值和拥挤度距离,更新粒子的速度和位置。
(6)重复步骤2-5,直到达到预设的停止条件。
⛄二、部分源代码
%% 14 UAVs
% 6 targets %目标
% 3 tasks on each target %在每个目标上的任务
% 2 functions %功能
% 8 constrains %约束
%%
clc;
clear;
close all;
tic
%% 无人机参数初始化
global NU NS NMM V N NT NM dim
NU=14; %无人机总数目
NT=6; %目标数
NS=8; %侦察无人机数目
NMM=3; %每个目标上的任务数
NM=NT*NMM; %总任务数
T=[36 49 12;70 47 25;25 15 45;62 70 56;54 42 78;61 39 41]; %目标的坐标
U_X=[73 91 41;94 92 42;90 37 45;5 57 12;20 0 32;1 68 45;90 74 72;11 90 61;73 76 12;69 20 10;52 46 42;46 98 41;92 86 62;79 4 3]; %飞机坐标
V=[0.1;0.12;0.12;0.11;0.1;0.12;0.11;0.11;0.16;0.1;0.12;0.13;0.09;0.11]; %无人机的速度
%% 粒子群参数初始化
MaxIt = 50; %最大迭代次数
N = 20; %种群规模
w = 0.75; %惯性权重系数
pro=0.7; %向拐点学习概率
c1 = 0.7; %个体学习因子,c1=c2代表个体经验与群体经验有同样重要的影响
c2 = 0.7; %全局学习因子
dim=6; %粒子的行数
%% 调用粒子群
[pg,gb,hhh,HHH]=PSO(MaxIt,pro,c1,c2);
toc
disp(['运行时间: ',num2str(toc)]);
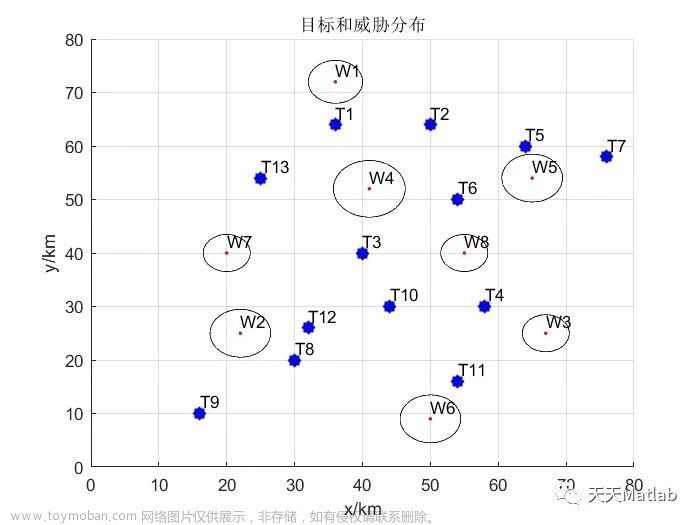
⛄三、运行结果







⛄四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]牛龙辉,陈海洋,季野彪.结合粒子群算法与任务分配协调策略的仓储多机器人任务分配[J].西安工程大学学报. 2020,34(06)文章来源:https://www.toymoban.com/news/detail-758270.html
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除文章来源地址https://www.toymoban.com/news/detail-758270.html
到了这里,关于【任务分配】多目标粒子群算法求解多无人机多任务路分配及路径规划(最短路程+最短时间)问题【含Matlab源码 3522期】的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!




](https://imgs.yssmx.com/Uploads/2024/04/861235-1.png)
](https://imgs.yssmx.com/Uploads/2024/04/857850-1.png)