第一节 矩阵的基本概念与特殊矩阵
一、基本概念
①矩阵
像如下图示的为矩阵,记为A=(aij)m*n

②同型矩阵及矩阵相等
若A、B为如下两个矩阵


如果A和B的行数和列数相等,那么A和B为同型矩阵,且A和B的元素相等(即:aij=bij),则称A和B相等
③伴随矩阵

设A为n阶矩阵(如上图所示),设A的行列式|A|,则A中aij的余子式为Mij,代数余子数为Aij,则A为如下所示,A即为A的伴随矩阵

④正交矩阵
若A为AA^T = A^TA = E,则称A为正交矩阵(E为单位矩阵,A^T为转置矩阵)
正交矩阵的性质:
(1)若A为正交矩阵,则|A|=1或|A|=-1
(2)若A为正交矩阵,则A可逆,A^T = A^-1
二、特殊矩阵
①零矩阵
设A=(aij)m*n,若∀aij=0,那么称为矩阵A为零矩阵,记为A=0
②n阶方阵
设A=(aij)m*n,若m=n,那么称为矩阵A为n阶方阵
③单位矩阵和数量矩阵
在矩阵的乘法中,有一种矩阵起着特殊的作用,如同数的乘法中的1,这种矩阵被称为单位矩阵,如图所示

数量矩阵就是对角线上元素都是同一个数值,其余元素都是零,如图所示

注:单位矩阵和数量矩阵必须是方阵
④转置矩阵

设A为m*n矩阵(如上图所示),将A的行和列元素进行交换(例如:aij和aji进行交换),得到如图,则称为转置矩阵,记为AT

⑤对角矩阵
如图所示的矩阵称为对角矩阵

第二节 矩阵的运算及其性质
一、矩阵的三则运算及其性质
(一)矩阵的三则运算
①矩阵的加减法

注:只有同阶的矩阵才能进行加减法
②矩阵与矩阵的乘法

其中cij=ai1 * bij + ai2 * b2j + … + ain * bnj
注:两个矩阵的内编号决定是否可相差,两个矩阵的外编号决定结果的行列数,例如Amn和Bmn无法相乘,Amn和Bnm结果为Cmm;
两个矩阵有顺序要求,例如A和B为两个矩阵,则AB≠BA
(二)矩阵的三则运算的性质
①A+B=B+A
②(A+B)+C=A+(B+C)
③(AB)C=A(BC)
④(k+l)A=kA+lA (k、l为常数)
⑤k(A+B)=kA+kB (k为常数)
⑥A(B+C)=AB+AC
⑦设A是mn矩阵,B,C分别为ns,n*l矩阵,则A(B┇C)=(AB┇AC)
注意:
①矩阵不满足分配率,但满足(A+B)^2 = A^2 + AB + BA + B^2
二、矩阵的转置运算及性质
(一)矩阵转置的定义

(二)矩阵转置的性质

第三节 矩阵的逆矩阵
一、矩阵理论产生的背景
①一元一次方程的解
一元一次方程ax=b的解分为如下两种情形:
(1)当a≠0时,因为(1/a)*a=1,所以将方程ax=b两边乘以1/a得a=b/a
(2)当a=0时,若b=0,则方程ax=b有无数个解;若b≠0,则方程ax=b无解
②矩阵方程的解
设A为m*n矩阵,AX=b表示线性方程组,其解的情形也有如下两种情形:
(1)设A为n阶方阵,且存在n阶矩阵B,使得BA=E,将方程组AX=b两边左乘B得BAX=Bb,即X=Bb,研究该情况方程组的解需要研究矩阵的逆矩阵理论
(2)设A为n阶矩阵但不存在矩阵B,使得BA=E;或A为m*n阵且m≠n,研究该情况方程组的解需要研究矩阵的秩的理论
二、逆矩阵的定义
设A是n阶矩阵,若存在 阶矩阵B使得BA=E(或AB=E),称矩阵A可逆矩阵B称为矩阵A的逆矩阵,记为B=A^-1
注意:
①若A可逆,则A^-1也是可逆的
②设A为n阶非零矩阵,由AB=AC不一定有B=C;设A可逆,则AB=AC,一定有B=C
三、关于矩阵的逆矩阵的两个问题
问题1:设A为n阶矩阵,A可逆的条件是什么?
问题2:设A为n阶可逆矩阵,如何求其逆矩阵A^-1?
四、矩阵可逆的充分必要条件(重要定理)
设A是n阶矩阵,则A可逆的充分必要条件是|A|=0.
注意:

五、逆矩阵的求法
(一)伴随矩阵法
若n阶矩阵A可逆,则A^-1 = (1/|A|) A* ,其中|A|为A的行列式,A*为A的伴随矩阵
(二)初等变换法求逆矩阵-思想体系与求法
1.方程组的三种同解变形
方程组的以下三种变形称为方程组的同解变形:
(1)对调两个方程;
(2)某个方程两边同乘以一个非零常数;
(3)某个方程的倍数加到另一个方程.
2.矩阵的初等变换
以下三种变换称为矩阵的初等行变换:
(1)对调矩阵的两行;
(2)矩阵的某行乘以非零常数 k;
(3)矩阵某行的倍数加到另一行
以下三种变换称为矩阵的初等列变换 :
(1)对调矩阵的两列;
(2)矩阵某列乘以非零常数 k;
(3)矩阵某列的倍数加到另一列.
矩阵的初等行变换和初等列变换统称为矩阵的初等变换
3.三种初等矩阵

4.与逆矩阵相关的三个问题
问题1: 设A为n阶可逆矩阵,A 否可以经过有限次初等行变换化为单位矩阵E?
解答: 若A 可逆,则A一定可以经过有限次初等行变换化为E
问题2: 设A是mnn 矩阵且r(A)=r,问A是否可以过有限次初等行变换化为
解答: 不一定
问题3 设A是m*n 矩阵,且r(A)=r,问A是否可以经过有限次初等变换化为
解答: 一定可以
5.初等变换法求逆矩阵




六、逆矩阵的性质


第四节 矩阵的秩
一、矩阵秩的概念
设A是m*n矩阵,矩阵A中任取r行和r列,元素按照原有次序排列构成的r阶行列式,称为矩阵A的r阶子式,矩阵A共有Crm、Crn个阶子式若至少有一个阶子式不为零但所有r十1阶子式(如果有)皆为零,称r为矩阵A的秩记为r(A)=r.
注意:

二、矩阵秩的求法
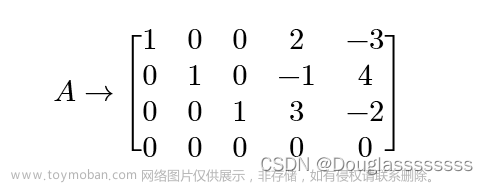
在方程组中,矩阵的秩本质上为方程组中约束条件的个数,而方程组约束条件的个数即经过方程组三种同解变形阶梯化后留下的方程个数,故对矩阵进行初等行变换阶梯化后非零行数即为矩阵的秩.如:

注意:
1.矩阵的秩本质上即为方程组约束条件的个数.
2.r(A)=0的充分必要条件是A=0
3.r(A)>=1的充分必要条件是A≠0
4.r(A)>=2的充分必要条件是A至少两行不成比例
三、矩阵秩的性质
性质1 r(A)=r(A^T) = r(A^TA) = r(AA^T ),其中A^T为A的转置矩阵
使用场景 出现A^TA 、或AA^T时使用
性质2 设A,B是同型矩阵,则r(A±B)<=r(A)+r(B).
使用场景 出现A+B,A-B或r(A)+r(B)时使用

使用场景 出现r(A),r(B),r(AB)时使用
性质4 设A,B分别为mn及ns矩阵,且AB=0,则r(A)+r(B)<=n
使用场景 出现AB=0时使用
性质5 设A是m*n矩阵,P、Q分别为m及n阶可逆矩阵,则r(A)=r(PA)=r(AQ)=r(PAQ)

使用场景 出现A*或Aij时使用

性质8 设A为n阶非零矩阵,则r(A)=1的充分必要条件是,存在非零向量α、β,使得得A=αβT,其中βT为β的转置矩阵
第五节 矩阵等价
一、矩阵等价的定义
设A,B是两个同型矩阵,若A经过有限次初等变换化为 B,称矩阵A与矩阵B等价
二、矩阵等价判别法
定理1 设A,B为同型矩阵,则AB是等价矩阵的充分必要条件是r(A)=r(B).
定理2 设A,B为同型矩阵,则A,B等价的充分必要条件是,存在可逆矩阵P,Q,使得PAQ=B.
注意:矩阵相等(第一节提到过)和矩阵等价(上述提到过)不同
矩阵笔记
① AB^T为矩阵, A^TB 为一个数(后边矩阵前边数),且A^TB 的值为矩阵AB^T的对角线,例如:

② 如果α、β为两个维数相同的列向量,且A=αβ^T, 则A^n = k^(n-1)A ,其中k = α^Tβ = β^Tα,例如:

③ 相似变换矩阵文章来源:https://www.toymoban.com/news/detail-758313.html

两个相似的矩阵有许多相同的性质:文章来源地址https://www.toymoban.com/news/detail-758313.html
- 两者的秩相等。
- 两者的行列式相等。
- 两者的迹数相等。
- 两者拥有同样的特征值,尽管相应的特征向量一般不同。
- 两者拥有同样的特征多项式。
- 两者拥有同样的初等因子。
到了这里,关于线性代数基础【2】矩阵的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!