FPGA实现CIC滤波器
上一节MATLAB CIC滤波器_小小低头哥的博客-CSDN博客介绍了如何使用MATLAB仿真不同要求的CIC滤波器,并对结果进行了分析。这次使用FPGA分别实现单级、多级CIC滤波器。
单级CIC滤波器的实现非常简单。根据
y
(
n
)
=
∑
k
=
0
M
−
1
x
(
n
−
k
)
=
x
(
n
)
−
x
(
n
−
M
)
+
∑
k
=
0
M
−
1
x
(
n
−
1
−
k
)
=
[
x
(
n
)
−
x
(
n
−
M
)
]
+
y
(
n
−
1
)
(1)
y(n)=\sum_{k=0}^{M-1}x(n-k)=x(n)-x(n-M)+\sum_{k=0}^{M-1}x(n-1-k)=[x(n)-x(n-M)]+y(n-1)\tag{1}
y(n)=k=0∑M−1x(n−k)=x(n)−x(n−M)+k=0∑M−1x(n−1−k)=[x(n)−x(n−M)]+y(n−1)(1)
可实现此单级滤波器。由于滤波器系数为0或者1,因此再滤波器结构中只需要加、减法及寄存器即可,从而可以使滤波器工作在极高的系统频率中。
1 单级CIC滤波器的FPGA设计
采用FPGA设计抽取倍数为5的抽取系统,采用5阶CIC滤波器作为抗混叠滤波器,并对抽取系统进行仿真测试。仿真频谱为1KHZ的正弦波信号,抽样频率为200KHZ,采用位数为10比特数据作为测试激励源,用MATLAB分析结果。
MATLAB信号产生函数和Modelsim仿真函数在前几节中给出了,此处直接给出FPGA代码
module SigCIC(
input rst, //复位信号
input clk, //FPGA系统时钟,频率为200KHZ
input signed[9:0] din, //输入数据频率为200KHZ
output reg r_flag, //输出数据有效指示信号
output reg signed[12:0] dout //滤波后的输出数据,5倍抽取后,频率为40KHZ
);
reg [2:0]count; //计数器
reg [3:0] i;
//x(n)-x(n-M)(M=5)分别对应din-din_reg[0]-din_reg[4]
reg signed[ 9:0] din_reg[4:0]; //寄存器
reg signed[12:0] dout_CIC; //CIC滤波器的每个输入数据对应的输出数据
//CIC滤波器过程
always @(posedge clk or posedge rst)
if(rst) begin
for(i=0;i<5;i=i+1) begin
din_reg[i] <= 10'd0; //初始化寄存器
end
dout_CIC <= 13'd0; //初始化输出
end
else begin
for(i=0;i<4;i=i+1) begin
din_reg[i+1] <= din_reg[i]; //将数据后移
end
din_reg[0] <= din;
dout_CIC <= dout_CIC + din - din_reg[4];//y(n) = y(n-1) + x(n)-x(n-M);
end
//抽取过程
always @(posedge clk or posedge rst)
if(rst) begin
count <= 3'd0;
dout <= 13'd0;
end
else if(count==3'd4) begin //每隔5次抽取一次
count <= 3'd0;
dout <= dout_CIC;
r_flag <= 1'd1;
end
else begin
count <= count + 1'd1;
r_flag <= 1'd0;
end
endmodule
1.1 结果展示及分析

Modelsim中的波形不够直观,接下来展示MATLAB中的展示的图形



由图不难发现仿真滤波后的信号频率为1KHZ,信号波形没有变化,但滤波后的数据速率降低为原来的1/5,仿真结果与期望结果一致。
2.多级CIC滤波器的FPGA实现
2.1 Noble恒等式
对于多级系统,包括线性系统、内插滤波器和抽取滤波器,可以在处理信号的流程中重新排列这3个部分的处理顺序,以便系统能够以更简便的方式实现。这就是所谓的Noble恒等式。
具体到多速率信号处理系统,如果线性系统F(zM)后面紧跟着M倍抽取滤波器,则式
F
(
Z
M
)
(
↓
M
)
=
(
↓
M
)
F
(
Z
)
(2)
F(Z^M)(↓M)=(↓M)F(Z) \tag{2}
F(ZM)(↓M)=(↓M)F(Z)(2)
这表明调换线性系统的抽取系统的处理顺序,及首先进行抽取,然后进行线性滤波,这样就可以将线性滤波器的长度降低到1/M,即滤波器的抽头数为原来的1/M。如果在线性系统F(ZL)前有L倍内插滤波器,则有式(3)成立。
(
↑
L
)
F
(
Z
L
)
=
F
(
Z
)
(
↑
L
)
(3)
(↑L)F(Z^L)=F(Z)(↑L)\tag{3}
(↑L)F(ZL)=F(Z)(↑L)(3)
也就是说,在内插时将线性系统放置在内插滤波器之前,就可以得到阶数降低为1/L的滤波器。
2.2 Hogenauer滤波器
根据CIC滤波器的原理,CIC滤波器可分为无反馈结构的FIR滤波器结构及有反馈结构的IIR滤波器。如果要用Noble恒等式原理改变多级CIC滤波器的结构,则需要采用有反馈结构的IIR滤波器。N级CIC滤波器的系统函数可表示为:
H
(
z
)
=
(
1
−
z
−
M
1
−
z
−
1
)
N
(4)
H(z)=(\frac{1-z^{-M}}{1-z^{-1}})^N\tag{4}
H(z)=(1−z−11−z−M)N(4)
根据式(4)可直接画出多级CIC滤波器的结构(以3级抽取滤波器为例),如图5(a)所示。根据易位定理,可以将图5(a)中的结构进行重新排列,得到图5(b)所示的结构。再根据Noble恒等式,改变抽取滤波器的位置,即可得到占用资源最少的多级CIC滤波器,如图5(c)所示,这种结构的滤波器被称为Hogenauer滤波器。按照同样的处理方法,可以得到多级Hogenauer滤波器内插滤波器,如图5(d)所示。

2.3多级CIC滤波器的FPGA设计
在FPGA上设计抽取倍数为5的抽取系统,采用5阶3级CIC滤波器作为抗混叠滤波器,并对抽取系统进行仿真测试,系统输入数据的位数为10比特,系统时钟与数据的频率相同。
仍然先用MATLAB产生200KHZ抽样的测试信号,给FPGA仿真使用。MATLAB以及FPGA仿真文件前面章节给出过,这里仍然只给出FPGA代码及仿真结果。
//顶层模块
module MultCIC(
input rst,
input clk,
input [ 9:0] Xin,
output [16:0] Yout,//滤波后的数据
output rdy
);
wire r_flag;
wire signed[16:0] Intout;
wire signed[16:0] dout;
//实例化积分器模块
Integrated u_Integrated(
.rst(rst),
.clk(clk),
.Xin(Xin),
.Intout(Intout)
);
//实例化抽取模块
Decimata u_Decimata(
.rst (rst),
.clk (clk),
.lin (Intout), //输入数据频率
.dout (dout), //滤波后数据
.r_flag(r_flag) //数据有效指示信号
);
//实例化梳状模块
Comb u_Comb(
.rst (rst), //复位信号
.clk (clk),
.r_flag (r_flag), //输入数据准备好信号
.Xin (dout), //输入数据
.Yout (Yout) //滤波后输出数据
);
assign rdy = r_flag;
endmodule
//积分模块
module Integrated(
input clk,
input rst,
input signed[ 9:0] Xin, //数据输入频率位2KHZ
output signed[16:0] Intout //滤波后的输出数据
);
wire signed[36:0] D1,D2,D3; //分别对应三个累加器的输出y1(n),y2(n),y3(n)
reg signed[36:0] d1,d2,d3; //寄存器 存储内容分别为三个累加器输出的延迟y1(n-1),y2(n-1),y3(n-1)
always @(posedge clk or posedge rst)
if(rst) begin //初始化
d1 <= 37'd0;
d2 <= 37'd0;
d3 <= 37'd0;
end
else begin
d1 <= D1;
d2 <= D2;
d3 <= D3;
end
assign D1 = (rst?37'd0:{{27{Xin[9]}},Xin} + d1);
assign D2 = (rst?37'd0:D1 + d2);
assign D3 = (rst?37'd0:D2 + d3);
assign Intout = D3[16:0];
endmodule
//抽取模块
module Decimata(
input rst,
input clk,
input signed[16:0] lin, //输入数据频率
output reg signed[16:0] dout, //滤波后数据
output reg r_flag //数据有效指示信号
);
reg [2:0] count; //计数器
always @(posedge clk or posedge rst)
if(rst) begin
count <= 3'd0;
r_flag <= 1'd0;
dout <= 17'd0;
end
else if(count == 3'd4) begin
count <= 3'd0;
r_flag <= 1'd1;
dout <= lin;
end
else begin
count <= count + 1'd1;
r_flag <= 1'd0;
dout <= dout;
end
endmodule
//梳状模块
module Comb(
input rst , //复位信号
input clk ,
input r_flag , //输入数据准备好信号
input signed[16:0] Xin,//输入数据
output signed[16:0] Yout//滤波后输出数据
);
wire signed[16:0] C1,C2; //每个累加器的输出
reg signed[16:0] c1,c2,c3,c4; //输入数据以及每个累计器输入的延迟
always @(posedge clk or posedge rst)
if(rst) begin
c1 <= 17'd0;
c2 <= 17'd0;
c3 <= 17'd0;
c4 <= 17'd0;
end
else if(r_flag) begin
c1 <= Xin;
c2 <= c1 ;
c3 <= C1 ;
c4 <= C2 ;
end
else begin
c1 <= c1 ;
c2 <= c2 ;
c3 <= c3 ;
end
assign C1 = (rst?17'd0:(c1-c2));
assign C2 = (rst?17'd0:(C1-c3));
assign Yout = (rst?17'd0:(C2-c4));
endmodule
2.4 仿真结果及分析

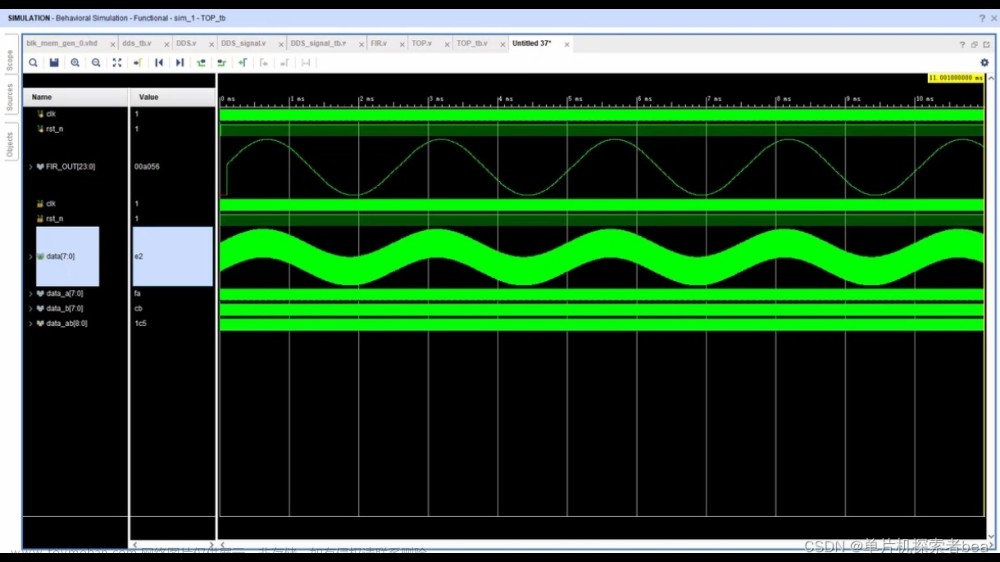
上图为Modelsim仿真结果,可以初步判断输出信号还不错。不过Modelsim观察不明白,用MATLAB读取此数据再观察

由上图不难发现,仿真前的1KHZ及30KHZ正弦波合成信号,经抽取滤波后,形成了的单一的1KHZ正弦波,切滤波后的数据速率降低为原来的1/5,仿真结果与期望结果相同。文章来源:https://www.toymoban.com/news/detail-758487.html
其实还有关于如何确定FPGA中中间级输出变量的字长问题,不过我目前没搞懂,就暂且不提了。文章来源地址https://www.toymoban.com/news/detail-758487.html
到了这里,关于FPGA实现CIC滤波器的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!