【算法每日一练]-图论（保姆级教程篇4（最短路，分层图） #最短路计数 #社交网络 #公园 #飞行路线 # 第二短路-Toy模板网

这篇具有很好参考价值的文章主要介绍了【算法每日一练]-图论（保姆级教程篇4（最短路，分层图） #最短路计数 #社交网络 #公园 #飞行路线 # 第二短路。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

今天知识点

di和sp求到每个点的最短路数

floyd求到点的最短路数和经过点的最短路数

求三点最短距离

每个点有多个状态，建立分层图

求第二短路

题目：最短路计数

思路：

题目：社交网络

思路：

题目：公园

思路：

题目：飞行路线

思路：

题目：第二短路

思路：

题目：最短路计数

【算法每日一练]-图论（保姆级教程篇4（最短路，分层图） #最短路计数 #社交网络 #公园 #飞行路线 # 第二短路,图论,算法,图论,数据结构,深度优先,c++,网络,leetcode

思路：

注意到每条路径的权值都是1，难怪结果会那么大。



dikjkstra和spfa版本最短路计数：
   if(dis[u]+1<dis[v]) ans[v]=ans[u],dis[v]=dis[u]+1
   else if(dis[u]+1==dis[v]) ans[v]+=ans[u]


1，维护最短路时产生的：那就是映射关系（因为引入的是周围点，相当于ans[v]=ans[cur]*1）
2，新最短路：发现了新的最短路就相加


也就是说我们只需要在更新路径的时候顺序更新记录最短路数的数组即可，相当于将两个dp式子一起执行了

#include <bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
const int N=1e6+5,M=2e6+5;
int mod=100003,n,m,tot=0;
int head[N],vis[N],dis[N],ans[N];
priority_queue<pii,vector<pii>,greater<pii>>Q;
struct node {int to;int next;}e[M*2];
void add(int u,int v){e[++tot]=(node){v,head[u]};head[u]=tot;}
void dijkstra(int s){
	memset(dis,0x3f,sizeof(dis));
	Q.push({0,s});dis[s]=0;ans[s]=1;
	while(!Q.empty()){
		int cur=Q.top().second;Q.pop();
		if(vis[cur])continue;//跳不跳无所谓，无非耗点时间
		vis[cur]=1;
		for(int i=head[cur];i;i=e[i].next)
		{
			int v=e[i].to;
			if(dis[cur]+1<dis[v])dis[v]=dis[cur]+1,ans[v]=ans[cur],Q.push({dis[v],v});//映射最短路(路过此点可以变短，那么最短路就和它有关)
			else if(dis[cur]+1==dis[v])ans[v]+=ans[cur],ans[v]%=mod;//新最短路(发现了另外的最短路就相加)
		}
	}
}
int main(){
	cin>>n>>m;int x,y;
	for(int i=1;i<=m;i++){
		scanf("%d%d",&x,&y);
		add(x,y);add(y,x);
	}
	dijkstra(1);
	//spfa(1);
	for(int i=1;i<=n;i++){
		cout<<ans[i]<<'\n';
	}
}

文章来源地址https://www.toymoban.com/news/detail-758609.html

//spfa版本：这个版本更快！！！！
void spfa(int s){
	memset(dis,0x3f,sizeof(dis));
	queue<int>q;vis[s]=1;
	q.push(s);dis[s]=0;ans[s]=1;
	while(!q.empty()){
		int cur=q.front();q.pop();
		vis[cur]=0;
		for(int i=head[cur];i;i=e[i].next){
			int v=e[i].to;
			if(dis[cur]+1<dis[v]){
			   dis[v]=dis[cur]+1;
			   ans[v]=ans[cur];
			   if(!vis[v])q.push(v),vis[v]=1;	
			}
			else if(dis[cur]+1==dis[v])ans[v]+=ans[cur],ans[v]%=mod;
		}
	}
}

题目：社交网络

思路：

点i的重要程度=∑从s到t的且经过i最短路条数/从s到t的最短路条数（s!=i，t!=i）

主要还是floyd算法，求出每个(i,j)对每个k的重要程度为ans[k]
求到某点时最短路径数：
1，只要最短路更新，那么最短路个数也要更新 e[i][j]=e[i][k]*e[k][j]
2，如果发现了新的最短路，那么就相加   e[i][j]+=e[i][k]*e[k][j];

#include <bits/stdc++.h>
using namespace std;   
typedef long long ll;
const int N=110;
ll INF,dis[N][N],e[N][N];//e[i][j]表示（i，j）的最短路径数
double ans[N];//每个点的重要程度
int main(){
	int n,m;ll x,y,z;
	cin>>n>>m;
	memset(dis,0x7f,sizeof(dis));
	INF=dis[1][1];//初始化INF无穷大
	for(int i=1;i<=m;i++){
		scanf("%lld%lld%lld",&x,&y,&z);
		dis[x][y]=dis[y][x]=z;
		e[x][y]=e[y][x]=1;//初始化e[i][j]
	}
	for(int i=1;i<=n;i++)  dis[i][i]=0;//对角线为0，但是不写也对其余任何边都没有影响，写不写随你
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++){
			if(dis[i][k]==INF||dis[k][j]==INF)continue;//有不通的就直接跳过
			if(dis[i][j]>dis[i][k]+dis[k][j]){
				dis[i][j]=dis[i][k]+dis[k][j];//每个边只会更新一次，即当前最优
				e[i][j]=e[i][k]*e[k][j];//只要最短路更新，则最短路对应的个数也要更新即可
				continue;
			}
			if(dis[i][j]==dis[i][k]+dis[k][j]){//找到了第二条最短路，就相加
				e[i][j]+=e[i][k]*e[k][j];
			}
		}
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++){
			if(i==j||j==k||i==k)continue;
			if(dis[i][j]==dis[i][k]+dis[k][j])//对k遍历每个（i，j）
				ans[k]+=(1.0*e[i][k]*e[k][j])/e[i][j];
		}
	for(int i=1;i<=n;i++)
		printf("%0.3f\n",ans[i]);
}

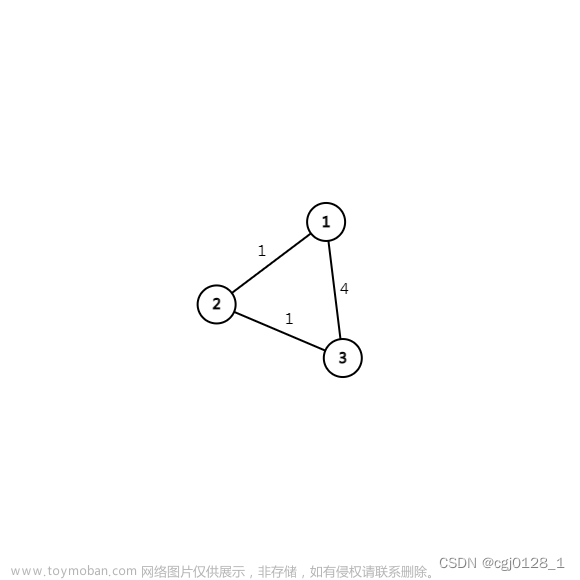
题目：公园

今天是六一节，小度去公园玩，公园一共 N 个景点，正巧看到朋友圈度度熊也在这个公园玩，于是他们约定好一块去景点 N。小度当前所在景点编号为 T，从一个景点到附近的景点需要消耗的体力是 TE，而度度熊所在景点编号为 F ，移动消耗为 FE。好朋友在一块，赶路都会开心很多，所以如果小度和度度熊一块移动(即在相同位置向相同方向移动)，每一步他俩的总消耗将会减少 S。
求他俩到景点 N 时，所需要的总消耗最少是多少？

输入：

输出：

思路：

其实注意到两个人的消耗是固定的，既然不知道在哪相遇，不妨把每个点都做中间相遇点试试，(你看看，出题人就是想让你暴力的)。

我们先对3个点找各自到其他点的最短距离，假如a点是相遇点，那么三个点(小度，小熊，终点)到此点a的最短距离×各自三个消耗(消耗怎么算？就看走了多长就行，因为每短的消耗是一样的)，这样的话，一种答案就出来了，然后找出最优答案即可。

其实，从这道题，你发现了什么？是不是找3个点的最近距离问题！

#include <bits/stdc++.h>    
using namespace std;   //暴力枚举
typedef pair<int,int> pa;
const int N=40005;
int dis[3][N],head[N];
int s1,s2,n,m;  
long long ans=1e17;
priority_queue<pa,vector<pa>,greater<pa>> Q;
struct node{int to;int next;}e[N*2]; //就是喜欢用链式前星
void add(int u,int v){
	static int i=0;i++;
	e[i].to=v;
	e[i].next=head[u];head[u]=i;
}
void dijkstra(int s,int dis[]){ //int dis[]=a[length],这样传参挺好的
	for(int i=0;i<=n;i++)dis[i]=40000;
	dis[s]=0;
	Q.push(make_pair(0,s));
	while(!Q.empty()){
		int u=Q.top().second;int dis_=Q.top().first;Q.pop();
		if(dis_!=dis[u]) continue;
		for(int i=head[u];i;i=e[i].next){
			int v=e[i].to;
			if(dis[v]>dis[u]+1)
				dis[v]=dis[u]+1,Q.push(make_pair(dis[v],v));
		}
	}	
}
int main(){
	long long e1,e2,e3; //之所以ll型，是因为dis是int型，运算时方便给ll型ans赋值（类型隐式转换）
	cin>>e1>>e2>>e3;  //e1，e2是两人的消耗，e3是减少的消耗：
	cin>>s1>>s2>>n>>m;//s1，s2是两个人的起点，n，m是景点数和边数
	int u,v;
	while(m--){
		scanf("%d %d",&u,&v);
		add(u,v);add(v,u);  //建边
	}
	dijkstra(s1,dis[0]); //寻找3个点到其余点的最短距离
	dijkstra(s2,dis[1]);
	dijkstra(n,dis[2]);
	for(int i=1;i<=n;i++){ //如果dis没有变说明这个点到不了，标记一下
		if(dis[0][i]==40000)dis[0][i]=-1;
		if(dis[1][i]==40000)dis[1][i]=-1;
		if(dis[2][i]==40000)dis[2][i]=-1;
	}
	for(int i=1;i<=n;i++){ 
		if(dis[0][i]!=-1&&dis[1][i]!=-1&&dis[2][i]!=-1) //3个点都要能到才算有效（能连起来）
		ans=min(ans,dis[0][i]*e1+dis[1][i]*e2+dis[2][i]*(e1+e2-e3)); //（ll*int）->ll类型
	}
	if(ans==1e17){cout<<-1;return 0;}//3个点没有一个公共交点，即3个点连不起来
	cout<<ans;
	return 0;
}

题目：飞行路线

思路：

一个图中任意两个点都可以权值变成0，最多有k次，我们常常建立k层的分层图，相邻层所有点建立权值为0的立体边，然后跑最短路即可

#include <bits/stdc++.h> 
using namespace std;
int cnt,head[110005];
int dis[110005];
bool vis[110005]; //标记当前白点，如果不想用vis，也可以判断取出元素的dis和dis数组中值是否一样
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>> > Q; //堆优化(first是值，second是下标)
struct Edge{ int to,w,next;}e[2500001];
void add(int u,int v,int w) { e[++cnt]=(Edge){v,w,head[u]}; head[u]=cnt;}
void Dijkstra(int s)//dijktra+堆优化
{
    memset(dis,0x3f,sizeof(dis));
    dis[s]=0;
    Q.push(make_pair(0,s));
    while(!Q.empty())  //必须用empty， size是求大小的，会慢一些 !!!
    {
		int u=Q.top().second; Q.pop();
		if(vis[u]) continue; //已经是白点的就跳过
	    vis[u]=1; //标记成白点
	    for(int i=head[u];i;i=e[i].next)
	    {
	        int v=e[i].to,w=e[i].w;
	        if(dis[v]>dis[u]+w) dis[v]=dis[u]+w,Q.push(make_pair(dis[v],v));
	    }
    }    
}

int main()
{
	int n,m,k,s,t;
	cin>>n>>m>>k>>s>>t; //城市数，航线数，免费次数，起始城市号，终点城市号
    int u,v,c;
    for(int i=0;i<m;++i)
    {
    	cin>>u>>v>>c;//两个城市航线，费用
    	for(int j=0;j<=k;++j){//建立每层图
    		add(u+j*n,v+j*n,c);
            add(v+j*n,u+j*n,c);
            if(j!=k){//第k层下面没有了，就别建了
            	add(u+j*n,v+(j+1)*n,0); //分层图：所有相邻层间：上下层u，v的权值为0
            	add(v+j*n,u+(j+1)*n,0);
			}
		}
    }
    for(int i=1;i<=k;++i)
	{
		add(t+(i-1)*n,t+i*n,0);
	}//处理奇葩数据
    Dijkstra(s);
    printf("%d",dis[t+k*n]);
    return 0;
}

题目：第二短路

思路：

#include<bits/stdc++.h>
using namespace std;   
typedef pair<int,int> pii;
const int N=5005,M=100005;
int n,m,tot,flag;
int head[N],d1[N],d2[N],vis[N];
priority_queue<pii,vector<pii>,greater<pii> > Q;
struct node{int to;int w;int next;}e[M*2];
void add(int u,int v,int w){e[++tot]=(node){v,w,head[u]};head[u]=tot;}
void dijkstra(int s){
	memset(d1,0x3f,sizeof(d1));//d1存放第一短路
	memset(d2,0x3f,sizeof(d2));//d2存放第二短路
	Q.push(make_pair(0,s));d1[s]=0;
	while(!Q.empty()){
		int cur=Q.top().second;Q.pop();
		if(vis[cur])continue;//vis数组可有可无，即便旧白点引入也掀不起变化，无非多走了几步
		vis[cur]=1;
		for(int i=head[cur];i;i=e[i].next){
			int v=e[i].to,w=e[i].w;flag=0;
			if(d1[cur]+w<d1[v])d2[v]=d1[v],d1[v]=d1[cur]+w,flag=1;//维护最短路，更新前的最短路就是次短路
			if(d1[cur]+w>d1[v]&&d1[cur]+w<d2[v])d2[v]=d1[cur]+w,flag=1;//最短路没有变化，更新次短路
			if(d2[cur]+w<d2[v])d2[v]=d2[cur]+w,flag=1;//维护次短路,如果d2[s]初始化成0,那么这个地方就出问题了
			if(flag)Q.push(make_pair(d1[v],v));
		}
	}
}
int main(){
	cin>>n>>m;int u,v,w;
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&u,&v,&w);
		add(u,v,w);add(v,u,w);
	}
	dijkstra(1);
	cout<<d2[n];
}

到了这里，关于【算法每日一练]-图论（保姆级教程篇4（最短路，分层图） #最短路计数 #社交网络 #公园 #飞行路线 # 第二短路的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！