(1)关于动态规划的定义:
之前买的假书害人捏......不过有个问题没说错,动态规划和递归很相似,但是动态规划利用分治法,把大问题转化为子任务,当计算出一个子任务的结果将储存起来,避免对于同一个子任务的重复计算
但其实根据某本书的写法,就是给递归套了一层存储的壳子......这个做法其实其中的一种,自上而下,在本质上仍然是将运算结果做一个简单的存储,
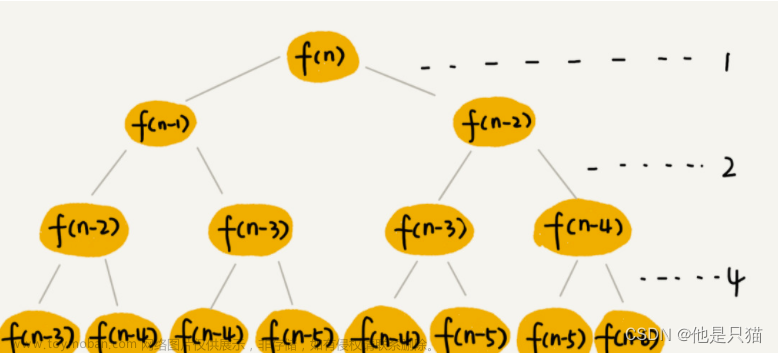
比如常用的斐波那契数列计算,使用自上而下反而更加直观,自下而上也不是不行,就很怪
而更加常用的动态规划可以理解为自下而上进行的,先去计算小任务,再去计算大任务的结果
这种动态规划一般需要我们写出一个dp状态转移方程,并且要用一定的顺序来由小到大计算(不一定是遍历矩阵捏)
另外,这种条件下我们想要输出结果,需要结合回溯法还有存储
(2)关于动态规划的举例(例题)
1.背包问题:
背包问题是除了斐波那契数列以外,最常用也是最简单的一种动态规划问题
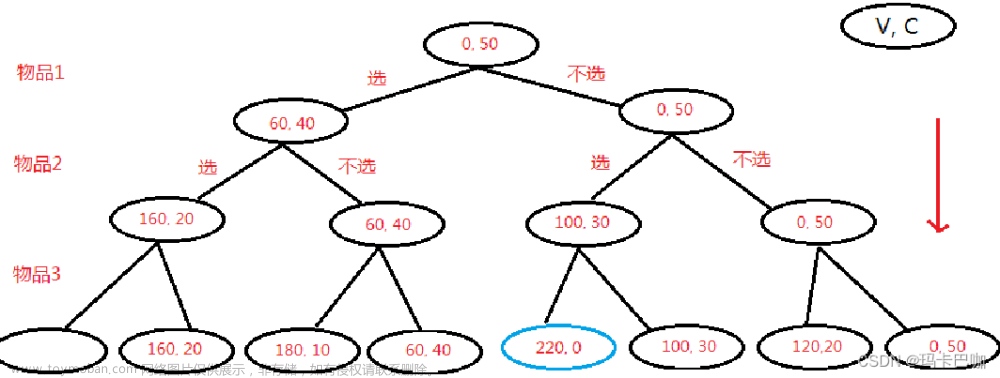
背包问题的描述,举例,当前有四件商品,编号为1234,所占空间为2345,价值为3456
如何有限的空间获取足够多的价值 (这种双限制的问题就该线性规划!<划掉>)
| 编号 | 1 | 2 | 3 | 4 |
| 所占空间 | 2 | 3 | 4 | 5 |
| 价值 | 3 | 4 | 5 | 6 |
2.处理思路/转移方程:
处理思路(这里先整理动态规划的部分)如果当前的剩余空间 j ,能装下当前这个商品 i,就判断一下能否购买这个,如果装不下就手动忽略这个
状态转移方程( f(i,j) 代表当前能购买前 i 个物体,剩余空间还有 j 条件下能获取到的最大价值)
当weight[i]>j(装不下的时候)
f(i,j)=f(i-1,j)
当weight[i]<=j(能装得下)
f(i,j)=max{ f(i-1 , j) , f( i-1 , j-weight[i])+value[i] }
截止条件为
i==0(意为没有商品可以购买的时候)
3.代码思路以及实现:
//提示想算出最优解是可行的,不过要进行回溯捏
//二维数组计算的原理为:(具体画个图)自下而上开始计算
//先把0的位置都初始化,然后从(1.1)开始往前,直到把所有的情况都计算出来,
// 然后直接读取最后一个位置
//之所以称之为动态,可能是因为某次计算出的结果会作为下一次计算的基数
void f(int x, int y) {
//初始化数组
int arr[50][50];
for (int i = 0; i < 50; i++) {
for (int j = 0; j < 50; j++) {
arr[i][j] = 0;
}
}
//然后开始往里面算
for (int i = 1; i <= x; i++) {
for (int j = 1; j <= y; j++) {
if (j >= weight[i]) {//注意这里是大于等于
int m1 = arr[i - 1][j];
int m2 = arr[i - 1][j - weight[i]] + value[i];
arr[i][j] = m1 > m2 ? m1 : m2;
}
else {
arr[i][j]= arr[i - 1][j];
}
}
}
//输出最终结果------------------------------------
cout << arr[x][y] << endl;
//遍历得到结果------------------------------------
for (int i = 0; i <= x; i++) {
for (int j = 0; j <= y; j++) {
cout << arr[i][j] << " ";
}
cout << endl;
}
}同时这里补充一个回溯的方法
//根据纯动态规划的获取方法(回溯)
//回溯的原理为:判断一下当前这个东西自己能否能装下,如果能装下
//看看当前的价值是否等于之前买下的情况,如果是,则确实是买下了这个东西
//如果不是,就代表自己没买
//此外,如果装不下,也默认自己没买
void findWhat(int x,int y) {//树组是上面运行完的现成数组,我们直接进行回溯
if (x >= 1) {
if (y >= weight[x]) {//代表可以买到
if (temp[x][y] == temp[x - 1][y - weight[x]] + value[x]) {
cout << "::" << x << endl;
findWhat(x - 1, y - weight[x]);
}
else {
findWhat(x - 1, y);
}
}
else {
findWhat(x - 1, y);
}
}
}2.最长回文子串
这道题来自于leetcode,具体的题解可以详见那边的讨论区

这道题其实肥肠简单,处理方法就是使用动态规划
状态转移方程为
A[i]==A[j] 且[i+1][j-1]为回文字串 则[i][j]也为回文字串,标记为1大致遍历的代码如下
for(int i=0;i<=n;i++) [i][i]
//设置初始条件,因为每个单独的字其实也可以视为回文子串
for(int i=2;i<=n;i+=2)
for(int j=0;j+i<=n;j++)
[j[j+i]若符合条件,则标记上这个,回文子串的长度为1+i原理:其实这个题还有点滑动窗口的影子在里面
因为状态转移方程中,判断一个部分是不是回文子串,除了要看两端是不是相等,就要看去掉两端以后内部是不是回文子串.因为这个与其称之为是自下而上,倒不如说是由内而外,
这种显然是不能做矩阵遍历的操作,我们需要结合一一下滑动窗口的思想
i+1其实代表的是这次视图判断的回文子串的长度,也就是一个窗口
我们通过不断地扩大窗口,来判断回文子串
3.最长公共字串
最长公共字串:存在一个最长的公共字串
注:这道题可以用kmp+窗口遍历的方式找到,但是复杂度为n²logn,太大了
使用动态规划的思想来处理更简单一些,多参考一下下面的第四题,很像
状态转移方程肥肠简单
// 若 x[i]==y[j] 则有c[i][j]=c[i-1][j-1]+1,,并且更新最大长度和末尾点
// 否则 清空为o
具体的代码实现为
代码如下
int arr2[10][10];
void maxSubString(string x,string y){//这个方法能得到最大公共字串的长度
int point=0;//最大字串末尾长度的位置
int MaxLength=0;//最大字串的末尾长度
//先赋值
for(int i=0;i<=9;i++)arr2[i][0]=arr2[0][i]=0;//先赋
//然后进行动态规划操作
for(int i=0;i<x.length();i++){
for(int j=0;j<y.length();j++){
if(i*j==0){
arr2[i][j]=0;
}else if(x[i]==y[j]){
arr2[i][j]=arr2[i-1][j-1]+1;
//判断并且实时更新末尾节点
if(arr2[i][j]>MaxLength){
MaxLength=arr2[i][j];
point=i;}
}else if(x[i]!=y[j]){
arr2[i][j]=0;
}
}
}
//按长度和坐标进行输出即可,毕竟已经知道公共字串在其中一个字符串的末尾节点了
for(int i=point-MaxLength+1;i<=point;i++)
cout<<x[i];
}4.最长公共子序列
最长公共子序列:假设存在两个序列AB,寻找到元素个数最大的公共子序列(注意,和最长公共字符串不是一个东西,这个不要求连续)
状态转移方程为
假设从1开始的字符串坐标位置
我们假设c[i,j]为两个字串末尾为i,j的时候,所存在的最大的公共子序列的元素数目
当i=0或者j=0的时候 c[i,j]=0;
否则 如果X[i]=Y[j] c[i,j]=c[i-1,j-1] + 1;
否则 c[i,j]=max{[i-1,j],[i,j-1]};具体的代码实现为
//关于公共子串问题
int arr[10][10];// 存储末尾为i,j的序列中,最大子序列的长度
int b[10][10]; // 存储公共元素的方位/path
void maxSub(string x,string y){
//先赋值
for(int i=0;i<=9;i++) b[i][0]=b[0][i]=arr[i][0]=arr[0][i]=0;//先赋
//然后进行动态规划操作
for(int i=0;i<x.length();i++){
for(int j=0;j<y.length();j++){
if(i*j==0){
arr[i][j]=0;
}else if(x[i]==y[j]){
arr[i][j]=arr[i-1][j-1]+1;
b[i][j]=1; //1代表的是这个就是最大公共序列的元素之一
}else if(x[i]!=y[j]){
arr[i][j]=max(arr[i-1][j],arr[i][j-1]);
if(arr[i-1][j]>=arr[i][j-1]) b[i][j]=2;//2代表是最大公共字串的元素在上面
else b[i][j]=3;//3代表是最大公共序列的元素在左面
}
}
}
}通过递归,以及b矩阵来寻找路径
//打印最大公共序列的方法
void printSub(int x,int y){
if(b[x][y]==0){ 到达边界情况,可以停下来了
return;
}else if(b[x][y]==1){ 当前这个元素就是最大公共子序列的元素
printSub(x-1,y-1);
cout<<arr[x][y];
}else if(b[x][y]==2){ 最大公共子序列的元素要往上找
printSub(x-1,y);
}else{ 最大公共子序列的元素要往左找
printSub(x,y-1);
}
}
5.钢条切割问题
钢条切割问题:假设有一段固定长度为n的钢条,切割成不同的段,可以卖出不同的价格,请问如何切割,能卖出最高价格?
这题其实很像是背包问题的逆情况,背包问题是塞东西,这是化整为零(笑)
第一种方法,自上而下,也就是递归套壳
f[i]代表长度为i的钢条切割所能得到的最大价格
price[x]代表长度为x的钢条的价格
s[i]=k记录分割点
int method(int i){
if f[i] !=-1
return f[i]
then
maxPrice = max{ f[1]+a(i-1),...f[k]+a(i-k),...f[i]+a(0)} (这里应该是for循环完成)
f[i]=max
s[i]=k //新增一个这个存储
return max;
}
然后想得到具体的解只需要用递归的方式s[i]即可
即为已知长度为i的分割点为k
如果最大的价值为不切割,即k=j,则完整的输出长度
否则,递归时分别计算出两个长度以后,继续递归第二种方法,状态转移方程,自下而上
其状态转移方程为
f[i]为长度为i的钢条能得到的最大收益
0 当i为0的时候
则状态转移方程为 f[i] =
max{ f[1]+a[i-1],.....,f[k]+a[i-k],....f[i]+a[0]}//用循环实现具体的代码实现则为
int dp(int n){
f[0]=0;
for i=1 to n
f[i] = max{ f[1]+a[i-1],.....,f[k]+a[i-k],....f[i]+a[0] } ; //(k也是利用1 to i实现的)
return f[n];
}解的重构方法为
void 回溯(int n){
//如果钢条长度为0,则无需处理
//如果钢条长度不是0
for(int i=1;i<=n;i++)
如果 f[n]=f[i]+a[n-i]
如果这里是切割成一个完整的加一个0
则直接输出
否则还是算出两个的长度,继续往下递归
}
6.堆合并问题/矩阵乘法问题
堆合并问题,又叫石子合并问题,可以抽象理解为一个一维数组,只允许相邻两个元素合并,一次合并的的花费等于两个元素的质量和.求出总的,最小的合并cost
如果可以,请给出合并方案
(值得注意的是,矩阵的乘法也同样是这个思路,就连回溯都是一毛一样的)
处理方法如下:
设C[i][j]从i到j的合并所需要的最小的花费
cut[i][j]=k,代表最佳的合并点为 i,k k+1,j
weight[i][j]i到j的总重量,也就是本次合并操作花费的力气
合并的状态方程较为简单,只要确保i<=j即可
c[i][j] = max{ c[i][k] + c[k+1][j] + weight[i][j] };
初始状态为c[i][i]=0,即为单个元素不存在合并花费这一说这道题其实和前面的最长回文字串一模一样的思路,因为这是从内到外的dp,则需要用到这种窗口遍历的方法,逐渐扩大窗口的大小,来得到每一个小的情况
代码实现如下
//处理堆合并问题的算法为
int ar[5]={3,5,2,3,4};
int C[5][5]; //用来存储这一步的最小花费
int weight[5][5];//用来储存重量,防止计算的时候耗费太多时间
int cut[5][5]; //用来存储切割位点
//最长回文子串和矩阵乘法的综合问题qwq
void stackMerge(){
//单一长度所需的合并花费肯定为0,因为根本不需要花费什么东西
for(int i=0;i<5;i++) C[i][i]=0;
//计算重量
for(int i=0;i<=4;i++){
for(int j=i+1;j<=4;j++){
weight[i][j]=0;
for(int x=i;x<=j;x++){
weight[i][j]+=ar[x];
}
}
}
for(int i=1;i<=4;i++){
for(int j=0;j+i<=4;j++){
int k;
int minCost=10000;
for(int x=j;x<j+i;x++){
if(C[j][x]+C[x+1][j+i]+weight[j][j+i]<=minCost){
k=x;
minCost=C[j][x]+C[x+1][j+i]+weight[j][j+i];
}
}
C[j][j+i]=minCost;
cut[j][j+i]=k;
}
}
cout<<C[0][4]<<endl;
}得到解的方法,其实是利用之前记录好的分割点,进行二叉树递归(这就很像是leetcode中的前序/后续+中序遍历处理二叉树的方式,都是已知分割点,进行分支构建二叉树)
在根据二叉树的形状,在合适的位置加上括号输出,就可以得到完整的操作表达式
//用递归处理回溯
//具体递归划分视情况而定,可以画个二叉树看看缺少什么东西
void howTodo(int x,int y){
if(x==y){
cout<<x;
}
else if(x+1==y){
cout<<"("<<x<<"*"<<y<<")";
}else{
cout<<"(";
howTodo(x , cut[x][y]);
howTodo(cut[x][y]+1 , y);
cout<<")";
}
}
7.子集和问题
问题描述:从集合A中找出一个子集B,B中元素的和为指定值key,如果不存在则输出提示
如果存在,请想办法进行回溯
子集和问题的处理方法如下
社F[i][j]=0/1 为截止到第i个元素,是否存在一个和为j的子序列
状态转移方程为
当a[i]>j的时候,代表不需要这个元素,F[i][j]=F[i-1][j]
当a[i]<=j的时候,可能算上这个元素刚好能凑出一个j,则前面i-1个元素中必定存在一个j-a[i]和的子集
如果不算这个元素,前面已经有了这样大小的和,则前面就存在一个j
则方程为 F[i-1][j] || F[i-1][j-a[i]]
前提条件,F[i][0]均设为1,任何子集存在空集代码处理如下
//关于子集和问题的处理
//问题描述:在集合A中寻找一个子集B,使得B中的集合等于一个固定的数值S
int n=5;
int A[7+1]={0,6,1,2,7,1,1,10};
int F[7+1][5+1];
//n为我们所需要的数值
//F[i][j]的含义为,截止到i,是否存在一个和为j,并且末尾元素为p[i]的子集,如果有就1,没有为0
//状态转移方程如下
//当A[i]>j的时候,
void dp(){
for(int i=0;i<=7;i++)
F[i][0]=1;
for(int i=1;i<=7;i++)
for(int j=1;j<=5;j++)
if(A[i]>j){//在前i-1位已经达到了满
F[i][j]=F[i-1][j];
}else{
F[i][j]=F[i-1][j]||F[i-1][j-A[i]];
}
cout<<(F[7][5]?"ok":"no solution")<<endl;
//使用回溯法判断
int i=7;int j=5;
while(i*j!=0){
if(F[i-1][j-A[i]]){
cout<<i<<"元素"<<A[i]<<endl;
i--;j-=A[i];
}else{
i--;
}
}
}判断解的情况,可以根据状态转移方程的情况是用回溯的方法进行处理
[ i - 1 ][ j ]代表没用到当前的点
[ i - 1 ][ j - A[i] ]代表已经用到了这个点
所以我们回溯可以利用循环,如果确实用到了当前的i点(即[ i - 1 ][ j - A[i] ]==1)
则输出这个点,并且i--,j-=A[i]
如果没用到这个点,则只需要i--,继续寻找下一个点即可文章来源:https://www.toymoban.com/news/detail-758610.html
(具体的回溯方法和上面写到一起了)文章来源地址https://www.toymoban.com/news/detail-758610.html
到了这里,关于[算法]动态规划以及常见例题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!