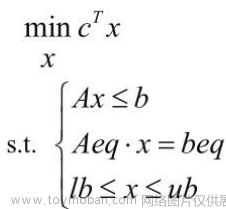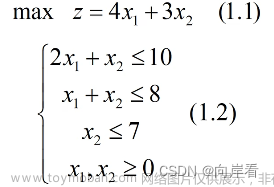目录
一、线性规划的标准形式
二、整数规划
二、整数规划之分支定界
1.概念
2、代码实现
三、整数规划之割平面法
1、基本思想
2、代码实现
四、整数规划之匈牙利算法(0-1)
1、适用情况
①0-1变量的使用
② 互斥问题
③固定费用问题
④指派问题
2、指派问题中匈牙利法
①步骤
②举例
3、代码实现
总结
一、线性规划的标准形式




求的是max,所以f中要加符号。f中是目标函数的系数
a表示的是不等式约束的系数(有不等号的,并且不等号为<)
b表示不等号后面的数
aeq表示线性约束的系数(有等号的系数)
beq表示等号后面的数
lb和ub表示最小值和最大值
(这里的zeros(3,1)表示创建3*1的数组,值都是0)
二、整数规划
1、概念



2、一般形式




二、整数规划之分支定界
1.概念




举例:

2、代码实现
matlab中代码:首先定义两个函数,然后再写一个测试脚本
function [x,fval,status] = intprog(f,A,B,I,Aeq,Beq,lb,ub,e)
%整数规划求解函数 intprog()
% 其中 f为目标函数向量
% A和B为不等式约束 Aeq与Beq为等式约束
% I为整数约束
% lb与ub分别为变量下界与上界
% x为最优解,fval为最优值
%例子:
% maximize 20 x1 + 10 x2
% S.T.
% 5 x1 + 4 x2 <=24
% 2 x1 + 5 x2 <=13
% x1, x2 >=0
% x1, x2是整数
% f=[-20, -10];
% A=[ 5 4; 2 5];
% B=[24; 13];
% lb=[0 0];
% ub=[inf inf];
% I=[1,2];
% e=0.000001;
% [x v s]= IP(f,A,B,I,[],[],lb,ub,,e)
% x = 4 1 v = -90.0000 s = 1
% 控制输入参数
if nargin < 9, e = 0.00001;
if nargin < 8, ub = [];
if nargin < 7, lb = [];
if nargin < 6, Beq = [];
if nargin < 5, Aeq = [];
if nargin < 4, I = [1:length(f)];
end, end, end, end, end, end
%求解整数规划对应的线性规划,判断是否有解
options = optimset('display','off');
[x0,fval0,exitflag] = linprog(f,A,B,Aeq,Beq,lb,ub,[],options);
if exitflag < 0
disp('没有合适整数解');
x = x0;
fval = fval0;
status = exitflag;
return;
else
%采用分支定界法求解
bound = inf;
[x,fval,status] = branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);
end
function [newx,newfval,status,newbound] = branchbound(f,A,B,I,x,fval,bound,Aeq,Beq,lb,ub,e)
% 分支定界法求解整数规划
% f,A,B,Aeq,Beq,lb,ub与线性规划相同
% I为整数限制变量的向量
% x为初始解,fval为初始值
options = optimset('display','off');
[x0,fval0,status0]=linprog(f,A,B,Aeq,Beq,lb,ub,[],options);
%递归中的最终退出条件
%无解或者解比现有上界大则返回原解
if status0 <= 0 || fval0 >= bound
newx = x;
newfval = fval;
newbound = bound;
status = status0;
return;
end
%是否为整数解,如果是整数解则返回
intindex = find(abs(x0(I) - round(x0(I))) > e);
if isempty(intindex) %判断是否为空值
newx(I) = round(x0(I));
newfval = fval0;
newbound = fval0;
status = 1;
return;
end
%当有非整可行解时,则进行分支求解
%此时必定会有整数解或空解
%找到第一个不满足整数要求的变量
n = I(intindex(1));
addA = zeros(1,length(f));
addA(n) = 1;
%构造第一个分支 x<=floor(x(n))
A = [A;addA];
B = [B,floor(x(n))];%向下取整
[x1,fval1,status1,bound1] = branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);
A(end,:) = [];
B(:,end) = [];
%解得第一个分支,若为更优解则替换,若不是则保持原状
status = status1;
if status1 > 0 && bound1 < bound
newx = x1;
newfval = fval1;
bound = fval1;
newbound = bound1;
else
newx = x0;
newfval = fval0;
newbound = bound;
end
%构造第二分支
A = [A;-addA];
B = [B,-ceil(x(n))];%向上取整
[x2,fval2,status2,bound2] = branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);
A(end,:) = [];
B(:,end) = [];
%解得第二分支,并与第一分支做比较,如果更优则替换
if status2 > 0 && bound2 < bound
status = status2;
newx = x2;
newfval = fval2;
newbound = bound2;
end
测试:
f=[-20 -10];
A=[5 4;2 5];
B=[24 13];
lb=[0 0];
[x,fval,status]= intprog(f,A,B,[1,2],[],[],lb)
三、整数规划之割平面法
1、基本思想




实例:
引入松弛变量 x7 x8 x9 x10
2、代码实现
定义一个函数DIvidePlane
function [intx,intf] = DividePlane(A,c,b,baseVector)
%功能:用割平面法求解整数规划
%调用格式:[intx,intf]=DividePlane(A,c,b,baseVector)
%其中, A:约束矩阵;
% c:目标函数系数向量;
% b:约束右端向量;
% baseVector:初始基向量;
% intx:目标函数取最值时的自变量值;
% intf:目标函数的最值;
sz = size(A);
nVia = sz(2);%获取有多少决策变量
n = sz(1);%获取有多少约束条件
xx = 1:nVia;
if length(baseVector) ~= n
disp('基变量的个数要与约束矩阵的行数相等!');
mx = NaN;
mf = NaN;
return;
end
M = 0;
sigma = -[transpose(c) zeros(1,(nVia-length(c)))];
xb = b;
%首先用单纯形法求出最优解
while 1
[maxs,ind] = max(sigma);
%--------------------用单纯形法求最优解--------------------------------------
if maxs <= 0 %当检验数均小于0时,求得最优解。
vr = find(c~=0 ,1,'last');
for l=1:vr
ele = find(baseVector == l,1);
if(isempty(ele))
mx(l) = 0;
else
mx(l)=xb(ele);
end
end
if max(abs(round(mx) - mx))<1.0e-7 %判断最优解是否为整数解,如果是整数解。
intx = mx;
intf = mx*c;
return;
else %如果最优解不是整数解时,构建切割方程
sz = size(A);
sr = sz(1);
sc = sz(2);
[max_x, index_x] = max(abs(round(mx) - mx));
[isB, num] = find(index_x == baseVector);
fi = xb(num) - floor(xb(num));
for i=1:(index_x-1)
Atmp(1,i) = A(num,i) - floor(A(num,i));
end
for i=(index_x+1):sc
Atmp(1,i) = A(num,i) - floor(A(num,i));
end
Atmp(1,index_x) = 0; %构建对偶单纯形法的初始表格
A = [A zeros(sr,1);-Atmp(1,:) 1];
xb = [xb;-fi];
baseVector = [baseVector sc+1];
sigma = [sigma 0];
%-------------------对偶单纯形法的迭代过程----------------------
while 1
%----------------------------------------------------------
if xb >= 0 %判断如果右端向量均大于0,求得最优解
if max(abs(round(xb) - xb))<1.0e-7 %如果用对偶单纯形法求得了整数解,则返回最优整数解
vr = find(c~=0 ,1,'last');
for l=1:vr
ele = find(baseVector == l,1);
if(isempty(ele))
mx_1(l) = 0;
else
mx_1(l)=xb(ele);
end
end
intx = mx_1;
intf = mx_1*c;
return;
else %如果对偶单纯形法求得的最优解不是整数解,继续添加切割方程
sz = size(A);
sr = sz(1);
sc = sz(2);
[max_x, index_x] = max(abs(round(mx_1) - mx_1));
[isB, num] = find(index_x == baseVector);
fi = xb(num) - floor(xb(num));
for i=1:(index_x-1)
Atmp(1,i) = A(num,i) - floor(A(num,i));
end
for i=(index_x+1):sc
Atmp(1,i) = A(num,i) - floor(A(num,i));
end
Atmp(1,index_x) = 0; %下一次对偶单纯形迭代的初始表格
A = [A zeros(sr,1);-Atmp(1,:) 1];
xb = [xb;-fi];
baseVector = [baseVector sc+1];
sigma = [sigma 0];
continue;
end
else %如果右端向量不全大于0,则进行对偶单纯形法的换基变量过程
minb_1 = inf;
chagB_1 = inf;
sA = size(A);
[br,idb] = min(xb);
for j=1:sA(2)
if A(idb,j)<0
bm = sigma(j)/A(idb,j);
if bm<minb_1
minb_1 = bm;
chagB_1 = j;
end
end
end
sigma = sigma -A(idb,:)*minb_1;
xb(idb) = xb(idb)/A(idb,chagB_1);
A(idb,:) = A(idb,:)/A(idb,chagB_1);
for i =1:sA(1)
if i ~= idb
xb(i) = xb(i)-A(i,chagB_1)*xb(idb);
A(i,:) = A(i,:) - A(i,chagB_1)*A(idb,:);
end
end
baseVector(idb) = chagB_1;
end
%------------------------------------------------------------
end
%--------------------对偶单纯形法的迭代过程---------------------
end
else %如果检验数有不小于0的,则进行单纯形算法的迭代过程
minb = inf;
chagB = inf;
for j=1:n
if A(j,ind)>0
bz = xb(j)/A(j,ind);
if bz<minb
minb = bz;
chagB = j;
end
end
end
sigma = sigma -A(chagB,:)*maxs/A(chagB,ind);
xb(chagB) = xb(chagB)/A(chagB,ind);
A(chagB,:) = A(chagB,:)/A(chagB,ind);
for i =1:n
if i ~= chagB
xb(i) = xb(i)-A(i,ind)*xb(chagB);
A(i,:) = A(i,:) - A(i,ind)*A(chagB,:);
end
end
baseVector(chagB) = ind;
end
M = M + 1;
if (M == 1000000)
disp('找不到最优解!');
mx = NaN;
minf = NaN;
return;
end
end举例:

>> c = [-1;-1]; % 不要加松弛变量
A = [-1 1 1 0;3 1 0 1]; % 加上松弛变量
b = [1;4];
[x fval] = DividePlane(A,c,b,[3 4]); % 松弛变量 3 4>> x
x =
1.0000 1.0000
>> maxz=-fval%求得最大值,加负号
maxz =
2
四、整数规划之匈牙利算法(0-1)
1、适用情况
①0-1变量的使用

② 互斥问题



③固定费用问题

④指派问题




2、指派问题中匈牙利法
①步骤




②举例




3、代码实现
 例子1
例子1
c = [3 8 2 10 3;8 7 2 9 7;6 4 2 7 5;8 4 2 3 5;9 10 6 9 10]
c = c(:); % 矩阵转换为向量
a = zeros(10,25);
for i = 1:5
a(i,(i-1)*5+1:5*i) = 1;
a(5+i,i:5:25) = 1;
end % 循环将指派问题转换为线性规划问题
b= ones(10,1); % 10个约束(5*2)
[x y] = linprog(c,[],[],a,b,zeros(25,1),ones(25,1));
X = reshape(x,5,5)
opt = y

例子2:

%% 指派问题(选择队员去进行游泳接力比赛)
clear;clc
c = [66.8 75.6 87 58.6 57.2 66 66.4 53 78 67.8 84.6 59.4 70 74.2 69.6 57.2 67.4 71 83.8 62.4]'; % 目标函数的系数矩阵(先列后行的写法)
intcon = [1:20]; % 整数变量的位置(一共20个决策变量,均为0-1整数变量)
% 线性不等式约束的系数矩阵和常数项向量(每个人只能入选四种泳姿之一,一共五个约束)
A = [1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1];
% A = zeros(5,20);
% for i = 1:5
% A(i, (4*i-3): 4*i) = 1;
% end
b = [1;1;1;1;1];
% 线性等式约束的系数矩阵和常数项向量 (每种泳姿有且仅有一人参加,一共四个约束)
Aeq = [1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0;
0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0;
0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0;
0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1];
% Aeq = [eye(4),eye(4),eye(4),eye(4),eye(4)]; % 或者写成 repmat(eye(4),1,5)
beq = [1;1;1;1];
lb = zeros(20,1); % 约束变量的范围下限
ub = ones(20,1); % 约束变量的范围上限
%最后调用intlinprog()函数
[x,fval] = intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)
% reshape(x,4,5)'
% 0 0 0 1 甲自由泳
% 1 0 0 0 乙蝶泳
% 0 1 0 0 丙仰泳
% 0 0 1 0 丁蛙泳
% 0 0 0 0 戊不参加
(感觉这个例子很实用,就引用过来了,要是有啥侵权,告诉我我删掉,不好意思)文章来源:https://www.toymoban.com/news/detail-758758.html
总结
以上为线性规划中算法代码,图片来自数学建模老哥课上ppt,仅为笔记。文章来源地址https://www.toymoban.com/news/detail-758758.html
到了这里,关于数学建模之matlab中线性规划的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!