实现二叉树的各种基本运算的算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了实现二叉树的各种基本运算的算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

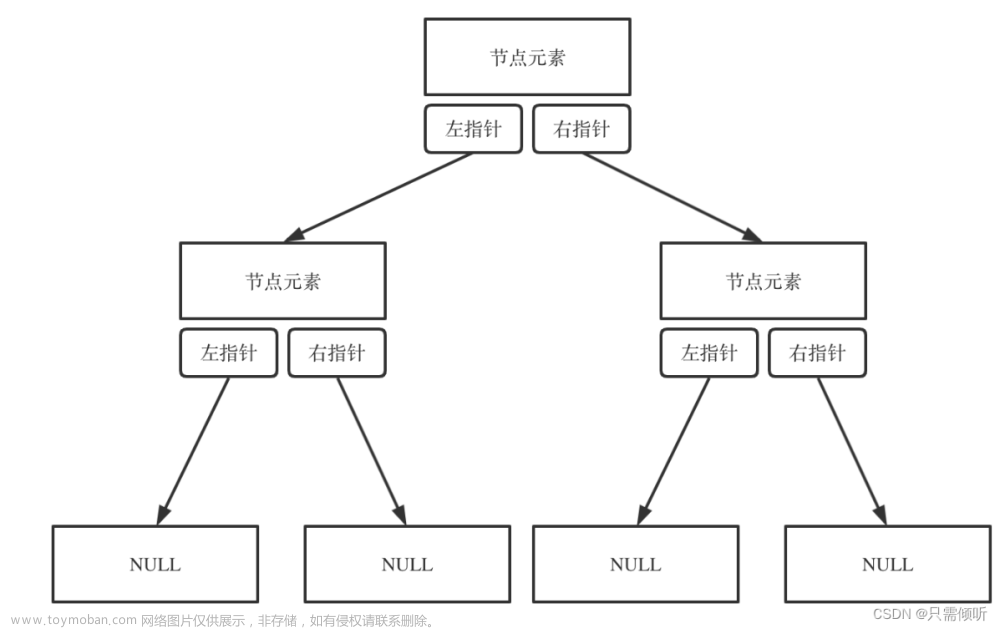
目的：领会二叉树的存储结构和掌握二叉树中各种基本运算算法的设计。

内容：编写一个程序btree.cpp，实现二叉树的各种基本运算，并在此基础上设计一个程序exp7-1.cpp完成以下功能。

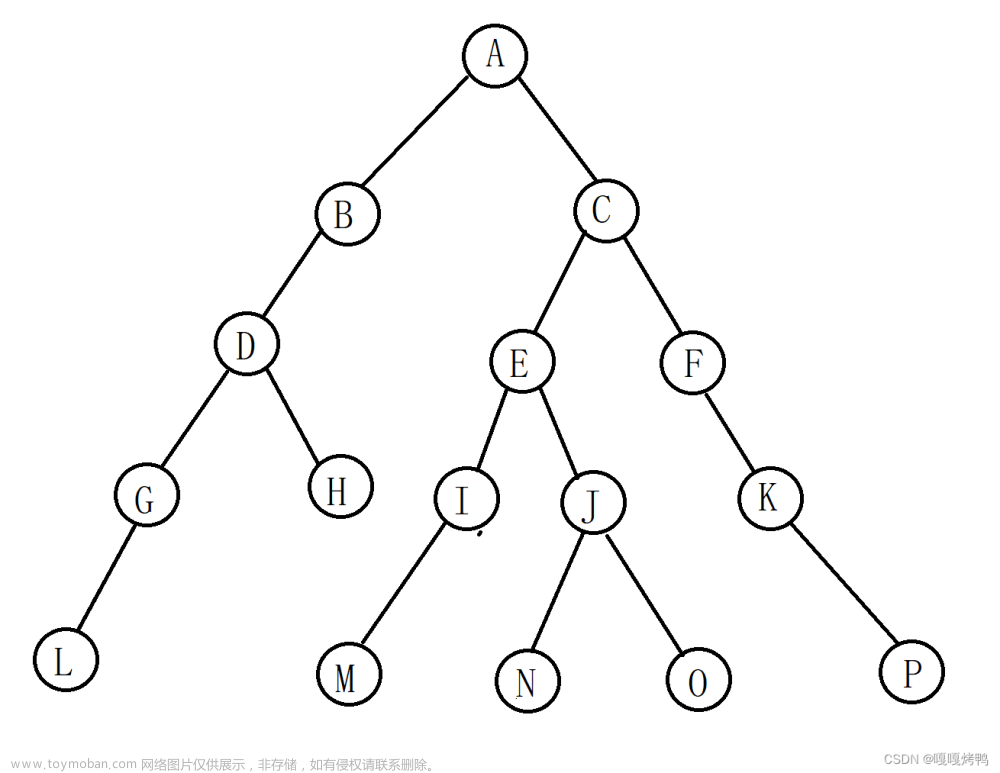
由图7.1所示的二叉树创建对应的二叉链存储结构b，该二叉树的括号表示串为“A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))”。
输出二叉树b。
输出‘H’结点的左、右孩子结点值。
输出二叉树b的高度。
释放二叉树b。

实现二叉树的各种基本运算的算法编写一个程序btree.cpp,实现二叉树的各种基本运,数据结构,数据结构

//计算机 小淇在敲代码  实现二叉树的各种基本运算的算法
#include<stdio.h>
#include<malloc.h>

#define MaxSize 100
typedef char ElemType;
typedef struct node
{
	ElemType data;          //数据元素
	struct node *lchild;    //指向左孩子结点
	struct node *rchild;    //指向右孩子结点
}BTNode;
//创建二叉树
void CreateBTree(BTNode *&b,char *str)
{
	BTNode *St[MaxSize],*p;
	int top=-1,k,j=0;char ch;
	b=NULL;
	ch=str[j];
	while(ch!='\0')
	{
		switch(ch)
		{
		case '(':top++;St[top]=p;k=1;break;
		case ')':top--;break;
		case ',':k=2;break;
		default:p=(BTNode *)malloc(sizeof(BTNode));
			p->data=ch;p->lchild=p->rchild=NULL;
			if(b==NULL)
				b=p;
			else
			{
				switch(k)
				{
				case 1:St[top]->lchild=p;break;
				case 2:St[top]->rchild=p;break;
				}
			}
		}
		j++;ch=str[j];
	}
}
//销毁二叉树
void DestroyBTree(BTNode *&b)
{
	if(b!=NULL)
	{
		DestroyBTree(b->lchild);
		DestroyBTree(b->rchild);
		free(b);
	}
}
//查找结点
BTNode *FindNode(BTNode *b,ElemType x)
{
	BTNode *p;
	if(b==NULL)
		return NULL;
	else if(b->data==x)
		return b;
	else
	{
		p=FindNode(b->lchild,x);
		if(p!=NULL)
			return p;
		else
			return FindNode(b->rchild,x);
	}
}
//找左孩子结点
BTNode *LchildNode(BTNode *p)
{
	return p->lchild;
}
//找右孩子结点
BTNode *RchildNode(BTNode *p)
{
	return p->rchild;
}
//求高度
int BTHeight(BTNode *b)
{
	int lchildh,rchildh;
	if(b==NULL)return(0);
	else
	{
		lchildh=BTHeight(b->lchild);
		rchildh=BTHeight(b->rchild);
		return (lchildh>rchildh)?(lchildh+1):(rchildh+1);
	}
}
//输出二叉树
void DispBTree(BTNode *b)
{
	if(b!=NULL)
	{
		printf("%c",b->data);
		if(b->lchild!=NULL||b->rchild!=NULL)
		{
			printf("(");
			DispBTree(b->lchild);
			if(b->rchild!=NULL)printf(",");
			DispBTree(b->rchild);
			printf(")");
		}
	}
}

//主函数
int main()
{
	BTNode *b,*p,*lp,*rp;
	printf("计算机 小淇在敲代码\n");
	printf("二叉树的基本运算如下：\n");
	printf("(1)创建二叉树\n");
	CreateBTree(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))");
	printf("(2)输出二叉树:");DispBTree(b);printf("\n");
	printf("(3)H结点:");
	p=FindNode(b,'H');
	if(p!=NULL)
	{
		lp=LchildNode(p);
		if(lp!=NULL)printf("左孩子: %c",lp->data);
		else printf("无左孩子");
		rp=RchildNode(p);
		if(rp!=NULL)printf("右孩子: %C",rp->data);
		else printf("");
	}
	printf("\n");
	printf("(4)二叉树b的高度：%d\n",BTHeight(b));
	printf("(5)释放二叉树b \n");
	DestroyBTree(b);
	return 1;
}

实现二叉树的各种基本运算的算法编写一个程序btree.cpp,实现二叉树的各种基本运,数据结构,数据结构