本部分视频所在地址：深度强化学习的理论与实践
3.1节 蒙特卡罗法简介
在其他学科中的蒙特卡罗法是一种抽样的方法。
如果状态转移概率是已知的，则是基于模型的方法。如果状态转移概率是未知的，则是免模型的方法。动态规划方法无法求解倒立摆问题，即无法处理没有状态转移概率的问题。蒙特卡罗法可以求解。
无偏估计量的理解参考：什么叫估计量的无偏性？一致性？有效性？、也可以参考下图（链接不好找，直接截图了）：
3.2节 蒙特卡罗策略评估
法1：ML拟合模拟数据法：本节不讲应用机器学习算法学习一个转移概率（这种方法是模拟出大量的数据，即下图中列出来的数据，然后使用一些ML如监督学习的方法来学习出P_head(s'|s,a)）
法2：免模型强化学习法（即蒙特卡罗方法）
经历完整的MDP序列：从初始状态S0或某一中间状态St，经过动作，奖励，状态，直到最终的终止状态ST。经历完整的MDP序列不一定从初始状态开始。
一个经历完整的MDP序列称为一次采样。
可以使用模拟程序来采样m条经历完整的MDP序列。
1）每条MDP序列的终止状态有可能一样有可能不一样，因为一个问题可能有多个终止状态
2）T1、T2、。。。Tm不是相同的
3）一个MDP序列可能从多种初始状态或多种中间状态开始。
上面的MDP序列中动作是根据π来决定的，如果要评估这个策略π，就要计算这个策略的动作值函数（或状态值函数），以下一动作值函数Q(s,a)为例
根据Q(s,a)的表达式是无法求出该期望的，因此希望使用样本的均值来近似该期望。此样本来自上面抽样出的MDP序列。
假设Gi(s,a)表示第i条MDP序列中从状态s开始执行动作a获得的累计折扣奖励。此时即可计算Q(s,a)。下式使用统计模拟出的m条MDP序列中得到的动作值函数均值来估计真实动作值函数的期望：
此处会出现一个问题（这个老师讲的不清楚，此处我听不懂，下面是瞎写的）：
s取自状态空间，a取自动作空间，(s,a)取自两个空间的乘积。对于m条MDP，如10000条MDP，10000sa的结果很大，采样效率较低
因此引入定义：
因此
好好看下下面这个算法，看懂了就懂了前面那些老师没讲清楚的内容。算法是很清晰的。
上面这个算法是先产生多个序列才去迭代算法
i表示当前统计到第i条链，因为第k条链上不一定有(s,a)
k不是第k条链，而是表示(s,a)在1,2，3，。。。i条链中出现的次数
算法3-1和算法3-2都是在维持一个这种的表格。
基于表格的方法，这种方法是针对离散的状态空间和动作空间。
动态规划算出来的解是精确地解，蒙特卡罗的解是估计出来的
3.3节 蒙特卡罗强化学习
上面的表是稀疏的，解决该问题提出来两种解决方式，如下：
1）保证每一个(s,a)都作为MDP链的初始状态。
2）在确定性策略中一些状态之后必然会发生某动作，其他动作将不会发生，软策略的改进在于，使确定性动作概率转为e，其他动作改为e/动作的个数。软策略中的其中一种称为e贪婪策略。
如何保证状态-动作对都已出现在MDP序列中？三种方法：
下面这个算法不用细致研究
下面这个算法中的过程：（），括号内容可以不在那里执行
3.4节 异策略蒙特卡罗法
两种策略的示例如下：
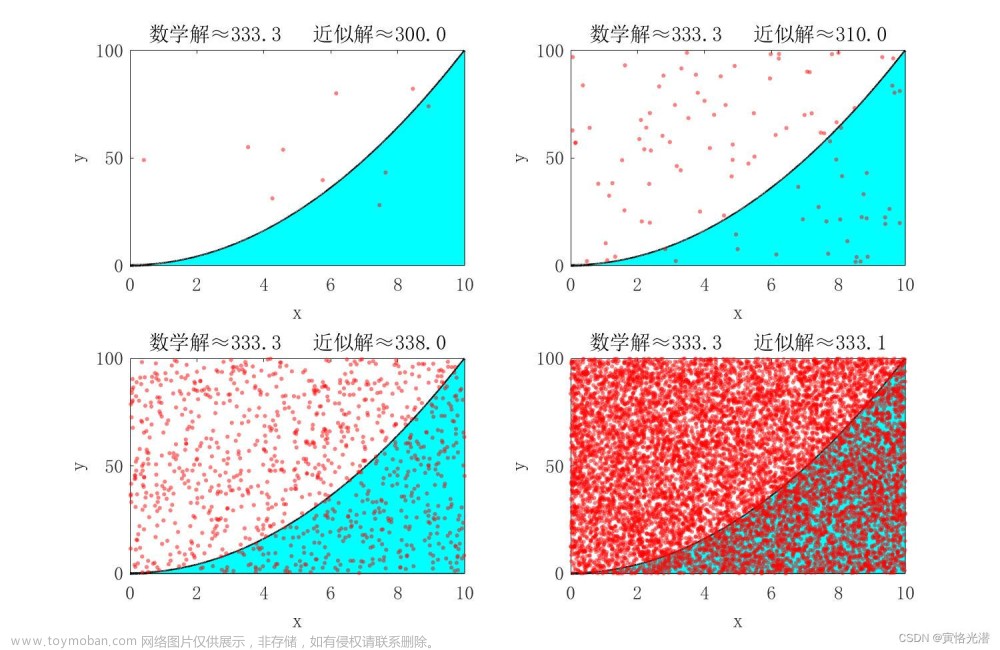
观察上图使用的均匀分布的采样方法来划分区间大小，其实在函数导数较大的地方也使用这种均匀划分区间的方法不太合适。因为此时矩形面试远大于曲线下方面积。因此有了一个想法，在导数大的地方划分的密集一点，在导数较小的地方划分的稀疏一点。因此有了重要性采样。
其中π策略是未知的，使用p分布来代替π分布是为了能实现不均衡采样，p分布可以认为就是已知的不均衡分布。上面的式子中π/p·f的取值会很困难，但是做到了最起码得采样是不均衡采样，即重要性采样。
已知一个行为策略π和一个状态转移概率p，如何计算一个已知的MDP序列存在的概率是多少？
ρ就叫重要性权重，这个值类似于积分中的π/p值
使用b分布来进行采样对行为策略π进行评估，需要最终乘以一个重要性权重。
重要性权重分：一般重要性采样和加权重要性采样
2、一般重要性采样的公式是下面第一个
上面算法中的异策略表现在待改进的策略与行为策略不一样。
尾部学习效应：是指重要性采样得到的MDP序列只学习后面一些状态和动作。文章来源：https://www.toymoban.com/news/detail-759171.html
对于确定性策略使用异策略效果不会很好。
文章来源地址https://www.toymoban.com/news/detail-759171.html
到了这里，关于学习深度强化学习---第3部分----RL蒙特卡罗相关算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
