给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
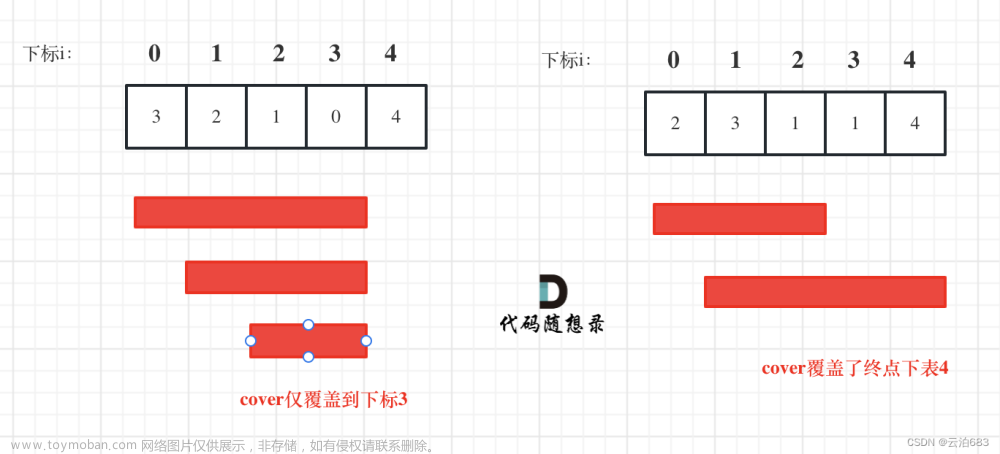
输入:nums = [2,3,1,1,4] 输出:true 解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4] 输出:false 解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
解析:
每次遍历,只需要贪心跳到最远即可。
class Solution {
public:
bool canJump(vector<int>& nums) {
int len = nums[0];
for(int i = 1;i < nums.size();i++)
{
if(len >= i)
{
len = max(len,nums[i]+i);
}
}
return len >= nums.size()-1;
}
};时间复杂度为O(n)
45. 跳跃游戏 II
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
-
0 <= j <= nums[i] i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4] 输出: 2 解释: 跳到最后一个位置的最小跳跃数是2。 从下标为 0 跳到下标为 1 的位置,跳1步,然后跳3步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4] 输出: 2
提示:
1 <= nums.length <= 1040 <= nums[i] <= 1000- 题目保证可以到达
nums[n-1]
解析:
这个是跳到最后一个位置的最小次数。
反向思想,从后向前,当前位置可以是哪个最先的下标跳跃而来的。
class Solution {
public:
int jump(vector<int>& nums) {
int p = nums.size()-1;
int ans = 0;
while(p > 0)
{
for(int i = 0;i < p;i++)
{
if(i+nums[i] >= p)
{
p = i;
ans++;
break;
}
}
}
return ans;
}
};时间复杂度为O(n*n);
在进行优化,我们可以这么想。我们每次跳到最远的。在从当前位置遍历到的第一次跳到最远的。
在这个最远的区间内,我们又可以更行更远的。以此类推,贪心正向遍历,时间复杂度为O(n)
class Solution {
public:
int jump(vector<int>& nums) {
int m = 0,r = 0;
int ans = 0;
for(int i = 0;i < nums.size()-1;i++) //最后一步不用跳
{
m = max(m,i+nums[i]);
if(i == r) // r为区间的左端点
{
r = m;
ans++;
}
}
return ans;
}
};2580. 统计将重叠区间合并成组的方案数
给你一个二维整数数组 ranges ,其中 ranges[i] = [starti, endi] 表示 starti 到 endi 之间(包括二者)的所有整数都包含在第 i 个区间中。
你需要将 ranges 分成 两个 组(可以为空),满足:
- 每个区间只属于一个组。
- 两个有 交集 的区间必须在 同一个 组内。
如果两个区间有至少 一个 公共整数,那么这两个区间是 有交集 的。
- 比方说,区间
[1, 3]和[2, 5]有交集,因为2和3在两个区间中都被包含。
请你返回将 ranges 划分成两个组的 总方案数 。由于答案可能很大,将它对 109 + 7 取余 后返回。
示例 1:
输入:ranges = [[6,10],[5,15]] 输出:2 解释: 两个区间有交集,所以它们必须在同一个组内。 所以有两种方案: - 将两个区间都放在第 1 个组中。 - 将两个区间都放在第 2 个组中。
示例 2:
输入:ranges = [[1,3],[10,20],[2,5],[4,8]] 输出:4 解释: 区间 [1,3] 和 [2,5] 有交集,所以它们必须在同一个组中。 同理,区间 [2,5] 和 [4,8] 也有交集,所以它们也必须在同一个组中。 所以总共有 4 种分组方案: - 所有区间都在第 1 组。 - 所有区间都在第 2 组。 - 区间 [1,3] ,[2,5] 和 [4,8] 在第 1 个组中,[10,20] 在第 2 个组中。 - 区间 [1,3] ,[2,5] 和 [4,8] 在第 2 个组中,[10,20] 在第 1 个组中。
提示:
1 <= ranges.length <= 105ranges[i].length == 20 <= starti <= endi <= 109
解析:
区间要不重和,所以不重和的区间有两种选择,去第一个还是去第二个。我们对左端点进行排排序。当前区间右端点判断是否和下一个区间的左端的有重合。如果没有,则可以看错新的全,他可以去第一个也可以去第二个。文章来源:https://www.toymoban.com/news/detail-759201.html
class Solution {
public:
const int MOD = 1e9 + 7;
int countWays(vector<vector<int>>& ranges) {
sort(ranges.begin(),ranges.end(),[](auto &a,auto &b)
{
return a[0] < b[0];
});
int ans = 2,max_r = ranges[0][1];
for(auto &p : ranges)
{
if(p[0] > max_r)
{
ans = ans*2%MOD;
}
max_r = max(max_r,p[1]);
}
return ans;
}
};时间复杂度为O(n*logn)文章来源地址https://www.toymoban.com/news/detail-759201.html
到了这里,关于跳跃游戏 + 45. 跳跃游戏 II的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!