1. Toy模板网首页
  2. > Toy博客

【数据结构与算法】Huffman编码/译码（C/C++）

9月前 作者：hiddenSharp429 分类：Toy博客 阅读(43) 违法举报

这篇具有很好参考价值的文章主要介绍了【数据结构与算法】Huffman编码/译码（C/C++）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

实践要求

1. 问题描述

利用哈夫曼编码进行信息通讯可以大大提高信道利用率，缩短信息传输时间，降低传输成本。但是，这要求在发送端通过一个编码系统对待传数据预先编码；在接收端将传来的数据进行译码(复原)。对于双工信道(即可以双向传输信息的信道)，每端都需要一个完整的编/译码系统。试为这样的信息收发站写一个哈夫曼码的编译码系统。

2. 基本要求

一个完整的系统应具有以下功能:

  1. I 初始化(Initialization)
    从终端读入字符集大小n，及n个字符和n个权值，建立哈夫曼树，并将它存于文件hfmtree中。
  2. C:编码(Coding)
    利用已建好的哈夫曼树(如不在内存，则从文件hfmtree中读 入)，对文件tobetrans中的正文进行编码，然后将结果存入codefile中。
  3. D:译码(Decoding)
    利用已建好的哈夫曼树将文件codefile中的代码进行译 码，结果存入文件textfile中。
  4. P:印代码文件(Print)
    将文件codefile以紧凑格式显示在终端上，每行50个代 码。同时将此字符形式的编码文件写入文件codeprint中。
  5. T:印哈夫曼树(Tree print)
    将已在内存中的哈夫曼树以直观的方式 树或凹入表行式)显示在终端上，同时将此字符形式的哈夫曼树写入文件treeprint中。

3. 测试数据

可能出现8种字符，其概率分别为0.05，0.29，0.07，0.80，0.14，0.23，0.03，0.11试设计赫夫曼编码。

3.1 input

请输入字符串集大小

8

请输入字符和权值 //用空格分离

a 5
b 29
c 7
d 8
e 14
f 23
g 3
h 11

3.2 output

若要输出"abc"这个字符串的Huffman编码
(正确的结果应为0001111010)

实践报告

1. 题目分析

说明程序设计的任务，强调的是程序要做什么，此外列出各成员分工

程序设计任务：设计一个Huffman编码译码系统，有I：初始化；C：编码；D：译码；P：印代码文件；T：印Huffman树五个功能模块。

2. 数据结构设计

说明程序用到的数据结构的定义，主程序的流程及各模块之间的层次关系

该程序主要用到的数据结构是Huffman树（最优二叉树）

主程序流程图

c++实现哈夫曼编码译码,算法与数据结构,C/C++,c语言,c++,算法

3. 程序设计

实现概要设计中的数据类型，对主程序、模块及主要操作写出伪代码，画出函数的调用关系

各模块伪代码

初始化

c++实现哈夫曼编码译码,算法与数据结构,C/C++,c语言,c++,算法

编码

c++实现哈夫曼编码译码,算法与数据结构,C/C++,c语言,c++,算法

解码

c++实现哈夫曼编码译码,算法与数据结构,C/C++,c语言,c++,算法

打印

c++实现哈夫曼编码译码,算法与数据结构,C/C++,c语言,c++,算法

打印并存入Huffman树

c++实现哈夫曼编码译码,算法与数据结构,C/C++,c语言,c++,算法

各函数层次关系图

Initialization

c++实现哈夫曼编码译码,算法与数据结构,C/C++,c语言,c++,算法

EnCode

c++实现哈夫曼编码译码,算法与数据结构,C/C++,c语言,c++,算法

DeCode

c++实现哈夫曼编码译码,算法与数据结构,C/C++,c语言,c++,算法

Tree

c++实现哈夫曼编码译码,算法与数据结构,C/C++,c语言,c++,算法

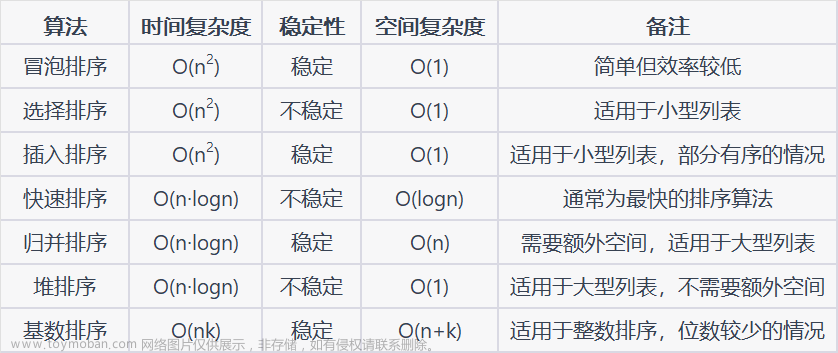
4. 调试分析

程序复杂度分析

1. 空间复杂度
o ( n ) o(n) o(n)
空间复杂度主要是由节点的内存空间和最小堆的内存空间所占据的空间所决定的，因此总的空间复杂度为O(n)。
2. 时间复杂度
O ( n l o g n ) O(nlogn) O(nlogn)
由于建立哈夫曼树的过程中需要使用最小堆来实现节点的排序和合并。最小堆的插入和删除操作都需要O(logn)的时间复杂度，而需要进行n-1次操作，因此总的时间复杂度为O(nlogn)

所遇到的问题的解决方法

  • 问题1:内存泄露问题，动态分配的空间未释放。
    解决:在函数解放使用free来释放动态分配的空间
  • 问题2:按格式读取文件信息
    解决:使用buffer和characters两个数组，buffer用于接收所有的txt文件中的内容，将buffer中有用的信息赋值给characters。

5. 测试结果

列出测试结果，包括输入和输出

测试结果一

先初始化将字符以及其权值存入txt文件中

c++实现哈夫曼编码译码,算法与数据结构,C/C++,c语言,c++,算法
c++实现哈夫曼编码译码,算法与数据结构,C/C++,c语言,c++,算法

再对其进行编码

c++实现哈夫曼编码译码,算法与数据结构,C/C++,c语言,c++,算法
c++实现哈夫曼编码译码,算法与数据结构,C/C++,c语言,c++,算法

对编码结果进行解码

c++实现哈夫曼编码译码,算法与数据结构,C/C++,c语言,c++,算法

打印Huffman树并存入txt中

c++实现哈夫曼编码译码,算法与数据结构,C/C++,c语言,c++,算法

6. 用户使用说明

给出主界面及主要功能界面

使用说明

首先初始化Huffman树，然后进行编码，编码后可选择译码也可以选择印代码文件或者印Huffman树。

7. 附录

源程序文件清单:
huffman.cpp
treeprint.txt
textfile.txt
hfmtree.txt
codefile.txt
codeprint.txt

8. 全部代码

huffman.cpp

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <iostream>

using namespace std;

// 定义哈夫曼树的节点结构体
typedef struct node
{
    int weight;         // 权值
    char character;     // 字符
    struct node *left;  // 左子树指针
    struct node *right; // 右子树指针
} Node;

// 定义哈夫曼树的节点类型
typedef Node *HuffmanTree;

// 定义哈夫曼树的节点最小堆
typedef struct heap
{
    int size;          // 堆的大小
    int capacity;      // 堆的容量
    HuffmanTree *data; // 堆数据存储指针
} MinHeap;

// 初始化最小堆
MinHeap *initMinHeap(int capacity)
{
    // 动态分配最小堆
    MinHeap *heap = (MinHeap *)malloc(sizeof(MinHeap));
    heap->capacity = capacity;
    heap->size = 0;
    heap->data = (HuffmanTree *)malloc(sizeof(HuffmanTree) * capacity);
    return heap;
}

// 最小堆中插入元素
void insert(MinHeap *heap, HuffmanTree node)
{
    if (heap->size >= heap->capacity)
    {
        return; // 如果堆已满，直接退出
    }
    heap->data[heap->size] = node;  // 将元素插入堆底
    int current = heap->size++;     // 更新堆大小
    int parent = (current - 1) / 2; // 父节点的下标
    // 自下往上调整堆，直到找到合适的位置插入新元素
    while (parent >= 0 && heap->data[current]->weight < heap->data[parent]->weight)
    {
        // 如果当前元素比父节点的权值小，则交换两个元素的位置
        HuffmanTree temp = heap->data[parent];
        heap->data[parent] = heap->data[current];
        heap->data[current] = temp;
        current = parent;
        parent = (current - 1) / 2;
    }
}

// 从最小堆中取出最小元素
HuffmanTree extractMin(MinHeap *heap)
{
    if (heap->size == 0) // 如果堆为空，直接返回空指针
    {
        return NULL;
    }
    HuffmanTree min = heap->data[0];          // 最小元素即为堆顶元素
    heap->data[0] = heap->data[--heap->size]; // 将堆底元素移到堆顶，并更新堆大小
    int current = 0;                          // 当前节点的下标
    int child = current * 2 + 1;              // 当前节点的左孩子的下标
    // 自上往下调整堆，直到找到合适的位置插入堆底元素
    while (child < heap->size) // 当前节点还有孩子节点
    {
        if (child + 1 < heap->size && heap->data[child + 1]->weight < heap->data[child]->weight)
        {
            child++; // 找到当前节点的左右孩子中较小的一个
        }
        if (heap->data[child]->weight < heap->data[current]->weight)
        {
            // 将当前节点和较小孩子节点交换位置
            HuffmanTree temp = heap->data[child];
            heap->data[child] = heap->data[current];
            heap->data[current] = temp;
            current = child;         // 更新当前节点的下标
            child = current * 2 + 1; // 更新当前节点的左孩子下标
        }
        else
        {
            break; // 如果已经满足最小堆的性质，则退出循环
        }
    }
    return min; // 返回被取出的最小元素
}

// 用最小堆构建哈夫曼树
HuffmanTree buildHuffmanTree(int *weights, char *characters, int n)
{
    // 初始化最小堆，将每个字符及其权重转换成节点，并插入堆中
    MinHeap *heap = initMinHeap(n);
    for (int i = 0; i < n; i++)
    {
        Node *node = (Node *)malloc(sizeof(Node));
        node->weight = weights[i];
        node->character = characters[i];
        node->left = NULL;
        node->right = NULL;
        insert(heap, node); // 将节点插入堆中
    }
    // 不断从最小堆中取出权重最小的两个节点，合并成一个新节点，再插入堆中
    while (heap->size > 1)
    {
        HuffmanTree left = extractMin(heap);  // 取出堆顶节点，即最小权重节点
        HuffmanTree right = extractMin(heap); // 再次取出最小权重节点
        Node *parent = (Node *)malloc(sizeof(Node));
        parent->weight = left->weight + right->weight; // 新节点的权重为左右节点的权重之和
        parent->left = left;                           // 将左节点作为新节点的左孩子
        parent->right = right;                         // 将右节点作为新节点的右孩子
        insert(heap, parent);                          // 将新节点插入堆中
    }
    HuffmanTree root = extractMin(heap); // 最后堆中只剩下根节点，即为哈夫曼树的根节点
    free(heap->data);                    // 释放堆数组占用的空间
    free(heap);                          // 释放最小堆结构体占用的空间
    return root;                         // 返回哈夫曼树的根节点指针
}
// 对单个字符进行编码模块
char *encodeChar(HuffmanTree root, char ch)
{
    static char code[100]; // 申请存储编码的空间
    static int index = 0;  // 记录编码位数

    if (root == NULL)
    {
        return NULL;
    }

    if (root->character == ch)
    {
        code[index] = '\0'; // 编码结尾
        index = 0;          // 编码位数归零
        return code;
    }

    code[index++] = '0';
    char *leftCode = encodeChar(root->left, ch);
    if (leftCode != NULL)
    {
        return leftCode;
    }

    index--; // 回溯
    code[index++] = '1';
    char *rightCode = encodeChar(root->right, ch);
    if (rightCode != NULL)
    {
        return rightCode;
    }

    index--; // 回溯
    return NULL;
}

// 对文本进行编码模块
char *encode(HuffmanTree root, char *text)
{
    char *result = (char *)malloc(strlen(text) * 100 * sizeof(char)); // 申请存储编码结果的空间
    result[0] = '\0';                                                 // 初始化
    for (int i = 0; i < strlen(text); i++)
    {
        char *code = encodeChar(root, text[i]); // 对单个字符编码
        if (code)
        {
            strcat(result, code); // 将编码拼接到结果中
        }
    }
    return result;
}

// 初始化函数
HuffmanTree initialization()
{
    int n; // 字符集大小
    printf("请输入字符集大小：\n");
    scanf("%d", &n);
    int *weights = (int *)malloc(sizeof(int) * n);       // 动态分配n个权重值
    char *characters = (char *)malloc(sizeof(char) * n); // 动态分配n个字符
    printf("请输入字符和权值：\n");
    for (int i = 0; i < n; i++)
    {
        scanf(" %c %d", &characters[i], &weights[i]);
    }
    HuffmanTree root = buildHuffmanTree(weights, characters, n);
    FILE *fp = fopen("hfmtree.txt", "w");
    fprintf(fp, "%d\n", n);
    for (int i = 0; i < n; i++)
    {
        fprintf(fp, "%c%s", characters[i], i == n - 1 ? "\n" : " ");
    }
    for (int i = 0; i < n; i++)
    {
        fprintf(fp, "%d%s", weights[i], i == n - 1 ? "\n" : " ");
    }
    fclose(fp);
    return root;
}

void EnCodeChar(HuffmanTree root)
{
    FILE *fp;
    char *characters;
    char buffer[100];
    int n;
    // 打开文件
    fp = fopen("hfmtree.txt", "r");
    if (fp == NULL)
    {
        printf("文件打开失败\n");
        exit(1);
    }
    // 读取第一行，获取字符集大小
    fscanf(fp, "%d", &n);
    // 分配空间
    characters = (char *)malloc(n * sizeof(char));
    // 读取第二行数据
    fgets(buffer, sizeof(characters) * 2, fp);
    fgets(buffer, sizeof(characters) * 2, fp);
    int i = 0;
    int j = 0;
    while (buffer[i] != NULL)
    {
        if (buffer[i] != ' ')
        {
            characters[j] = buffer[i];
            j++;
        }
        i++;
    }
    fclose(fp);
    for (int i = 0; i < n; i++)
    {
        int index = 0;
        char *res = encodeChar(root, characters[i]);
        printf("%c: %s\n", characters[i], res);
    }
}

void EnCode(HuffmanTree root)
{
    char tobetrans[100];
    char *result;
    printf("请输入一个字符串：\n");
    scanf("%s", tobetrans); // 读取输入的字符串，存储到字符数组中
    result = encode(root, tobetrans);
    printf("%s\n", result);
    FILE *fp = fopen("codefile.txt", "w");
    for (int i = 0; i < strlen(result); i++)
    {
        fprintf(fp, "%c", result[i]);
    }
    fclose(fp);
}

char DeCodeChar(HuffmanTree root, char *code)
{
    HuffmanTree p = root;
    while (*code != '\0')
    {
        if (*code == '0')
        {
            p = p->left;
        }
        else if (*code == '1')
        {
            p = p->right;
        }
        if (p->left == NULL && p->right == NULL)
        {
            return p->character;
        }
        code++;
    }
    return '\0';
}

void DeCode(HuffmanTree root)
{
    // 读取译码文件
    FILE *fp_code = fopen("codefile.txt", "r");
    char *code = (char *)malloc(1000 * sizeof(char)); // 申请存储代码的空间
    fscanf(fp_code, "%s", code);                      // 读取代码
    fclose(fp_code);

    // 译码
    char *text = (char *)malloc(1000 * sizeof(char)); // 申请存储译文的空间
    int i = 0, j = 0;
    while (code[i] != '\0')
    {
        char *tmp = (char *)malloc(100 * sizeof(char)); // 申请临时空间存储单个字符的编码
        int k = 0;
        while (DeCodeChar(root, tmp) == '\0')
        {
            tmp[k++] = code[i++];
        }
        text[j++] = DeCodeChar(root, tmp); // 译码并存储译文
        free(tmp);                         // 释放临时空间
    }
    text[j] = '\0';
    // 存储译文到文件中
    FILE *fp_text = fopen("textfile.txt", "w");
    fprintf(fp_text, "%s", text);
    fclose(fp_text);
    // 释放申请的空间
    free(code);
    free(text);
}

void Print()
{
    FILE *fp;
    char buffer[100];
    fp = fopen("codefile.txt", "r");
    if (fp == NULL)
    {
        printf("文件打开失败\n");
        exit(1);
    }
    // 读取数据
    fgets(buffer, 100, fp);
    printf("%s", buffer);
    fclose(fp);
    fp = fopen("codeprint.txt", "w");
    for (int i = 0; i < strlen(buffer); i++)
    {
        fprintf(fp, "%c", buffer[i]);
    }
    fclose(fp);
}

// 打印哈夫曼树的函数
void PrintHfmTree(FILE *file, HuffmanTree root, int level, char *prefix, int is_last)
{
    // 如果根节点为空，则返回
    if (root == NULL)
    {
        return;
    }
    // 打印当前节点的值
    printf("%s", prefix);
    printf(is_last ? "└── " : "├── ");
    printf("(%c:%d)\n", root->character, root->weight);
    fprintf(file, "%s", prefix);
    fprintf(file, is_last ? "└── " : "├── ");
    fprintf(file, "(%c:%d)\n", root->character, root->weight);

    // 更新前缀
    char new_prefix[128];
    sprintf(new_prefix, "%s%s", prefix, is_last ? "    " : "│   ");

    // 递归打印左右子树
    PrintHfmTree(file, root->left, level + 1, new_prefix, (root->right == NULL));
    PrintHfmTree(file, root->right, level + 1, new_prefix, 1);
}

void Tree(HuffmanTree root)
{
    // 打开文件treeprint
    FILE *file = fopen("treeprint.txt", "w");
    // 调用打印函数打印哈夫曼树并写入文件
    PrintHfmTree(file, root, 0, "", 1);
    // 关闭文件
    fclose(file);
}

HuffmanTree root = nullptr; // 将huffman树根设置为全局变量

void Window()
{
    char choice;
    char exit_choice;
    while (1)
    {
        printf("请选择您的操作：\n");
        printf("I. 初始化\n");
        printf("C. 编码\n");
        printf("D. 译码\n");
        printf("P. 印代码文件\n");
        printf("T. 印哈夫曼树\n");
        printf("E. 退出\n");
        scanf(" %c", &choice); // 加上空格忽略换行符

        switch (choice)
        {
        case 'I':
            printf("您选择了初始化操作。\n");
            root = initialization();
            break;
        case 'C':
            if (root == NULL)
            {
                printf("请先进行初始化操作！\n");
                break;
            }
            printf("您选择了编码操作。\n");
            EnCode(root);
            break;
        case 'D':
            if (root == NULL)
            {
                printf("请先进行初始化操作！\n");
                break;
            }
            printf("您选择了译码操作。\n");
            DeCode(root);
            break;
        case 'P':
            printf("您选择了打印操作。\n");
            Print();
            break;
        case 'T':
            printf("您选择了打印操作。\n");
            Tree(root);
            break;
        case 'E':
            printf("您确定要退出吗？按E键确认退出，按其他键返回上级菜单。\n");
            scanf(" %c", &exit_choice); // 加上空格忽略换行符
            if (exit_choice == 'E' || exit_choice == 'e')
            {
                printf("谢谢使用，再见！\n");
                return;
            }
            break;
        default:
            printf("无效的选择，请重新选择。\n");
            break;
        }
    }
}

int main()
{
    Window();
    return 0;
}

codefile.txt

0001111010

codeprint.txt

0001111010

hfmtree.txt

8
a b c d e f g h
5 29 7 8 14 23 3 11

textfile.txt

abc

treeprint.txt

└── (
:100)
    ├── (
:42)
    │   ├── (
:19)
    │   │   ├── (
:8)
    │   │   │   ├── (g:3)
    │   │   │   └── (a:5)
    │   │   └── (h:11)
    │   └── (f:23)
    └── (
:58)
        ├── (
:29)
        │   ├── (e:14)
        │   └── (
:15)
        │       ├── (c:7)
        │       └── (d:8)
        └── (b:29)

结束语

  因为是算法小菜，所以提供的方法和思路可能不是很好，请多多包涵~如果有疑问欢迎大家留言讨论，你如果觉得这篇文章对你有帮助可以给我一个免费的赞吗？我们之间的交流是我最大的动力！文章来源地址https://www.toymoban.com/news/detail-759720.html

到了这里，关于【数据结构与算法】Huffman编码/译码（C/C++）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • 浙大数据结构第五周之05-树9 Huffman Codes

    In 1953, David A. Huffman published his paper \\\"A Method for the Construction of Minimum-Redundancy Codes\\\", and hence printed his name in the history of computer science. As a professor who gives the final exam problem on Huffman codes, I am encountering a big problem: the Huffman codes are NOT unique. For example, given a string \\\"aaaxuaxz\\\", we can observe th

    2024年02月15日
    浏览(61)
  • 【数据结构与算法】哈夫曼编码（最优二叉树）实现

    【数据结构与算法】哈夫曼编码（最优二叉树）实现

    哈夫曼编码 等长编码：占的位置一样 变长编码（不等长编码）：经常使用的编码比较短，不常用的比较短 最优：总长度最短 最优的要求：占用空间尽可能短，不占用多余空间，且不能有二义性 这里给出哈夫曼二叉树的实现： HuffmanTree.h: 测试数据（主函数）： 运行结果截图

    2024年02月16日
    浏览(46)

  • 数据结构与算法之数组: Leetcode 89. 格雷编码 (Typescript版)

    格雷编码 https://leetcode.cn/problems/gray-code/ 描述 n 位格雷码序列 是一个由 2n 个整数组成的序列，其中： 每个整数都在范围 [0, 2n - 1] 内（含 0 和 2n - 1） 第一个整数是 0 一个整数在序列中出现 不超过一次 每对 相邻 整数的二进制表示 恰好一位不同 ，且 第一个 和 最后一个 整数

    2024年02月02日
    浏览(42)
  • 【数据结构与算法】哈夫曼编码（最优二叉树实现

    【数据结构与算法】哈夫曼编码（最优二叉树实现

    哈夫曼编码 等长编码：占的位置一样 变长编码（不等长编码）：经常使用的编码比较短，不常用的比较短 最优：总长度最短 最优的要求：占用空间尽可能短，不占用多余空间，且不能有二义性 这里给出哈夫曼二叉树的实现： HuffmanTree.h: 测试数据（主函数）： 运行结果截图

    2024年02月16日
    浏览(44)
  • 【数据结构 】哈夫曼编译码器

    【数据结构 】哈夫曼编译码器

    利用哈夫曼编码进行信息通信可大大提高信道利用率，缩短信息传输时间，降低传输成本。 要求：在发送端通过一个编码系统对待传数据预先编码；在接收端将传入的数据进行译码（复原）。对于双工信道(即可以双向传输信息的信道)，每端都需要个完整的编/译码系统。试为

    2024年01月18日
    浏览(45)
  • C语言---数据结构实验---哈夫曼树及哈夫曼编码的算法实现---图的基本操作

    C语言---数据结构实验---哈夫曼树及哈夫曼编码的算法实现---图的基本操作

    本篇实验代码非本人写，代码源自外部，经调试解决了部分warning和error后在本地vs上可以正常运行，如有运行失败可换至vs 未来会重构实现该两个实验 内容要求： 1、初始化(Init)：能够对输入的任意长度的字符串s进行统计，统计每个字符的频度，并建立哈夫曼树 2、建立编码

    2024年02月13日
    浏览(53)
  • 霍夫曼（Huffman）编码算法详解之C语言版

    霍夫曼（Huffman）编码算法详解之C语言版

    霍夫曼(Huffman)树是一类带权路径长度最短的二叉树树。Huffman树的一个非常重要的应用就是进行Huffman编码以得到0-1码流进行快速传输。 在电报收发等数据通讯中，常需要将传送的文字转换成由二进制字符0、1组成的字符串来传输。为了使收发的速度提高，就要求电文编码要尽

    2024年02月07日
    浏览(30)
  • 【C++】数据结构与算法：常用排序算法

    【C++】数据结构与算法：常用排序算法

    😏 ★,° :.☆(￣▽￣)/$: .°★ 😏 这篇文章主要介绍常用排序算法。 学其所用，用其所学。——梁启超 欢迎来到我的博客，一起学习，共同进步。 喜欢的朋友可以关注一下，下次更新不迷路🥞 排序算法是计算机科学中常见的一类算法，用于将一组数据按照特定的顺序进行排

    2024年02月14日
    浏览(46)
  • 【数据结构与算法C++实现】3、排序算法

    【数据结构与算法C++实现】3、排序算法

    原视频为左程云的B站教学 外层循环 ：n个数需要冒n-1个泡上去，剩下的一个必然是最小的。所以外层循环执行n-1轮 内层循环 ：比大小，第1个泡需要比n-1次，第2个泡,比较n-2次… 选择： 每次从待排序序列中选择 最小的一个 放在已排序序列的后一个位置 原理类似于对扑克牌

    2024年02月11日
    浏览(56)
  • C++数据结构与算法——哈希表

    C++数据结构与算法——哈希表

    C++第二阶段——数据结构和算法，之前学过一点点数据结构，当时是基于Python来学习的，现在基于C++查漏补缺，尤其是树的部分。这一部分计划一个月，主要利用代码随想录来学习，刷题使用力扣网站，不定时更新，欢迎关注！ 给定两个字符串 s 和 t ，编写一个函数来判断

    2024年02月19日
    浏览(56)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包