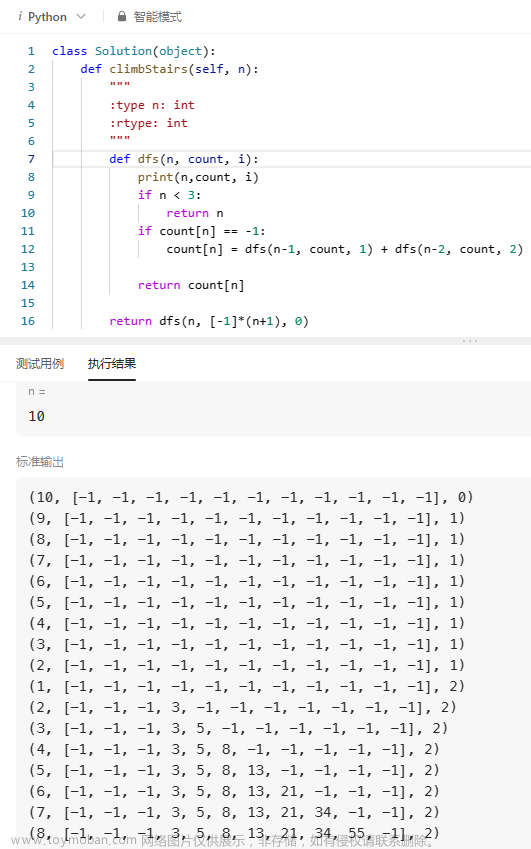
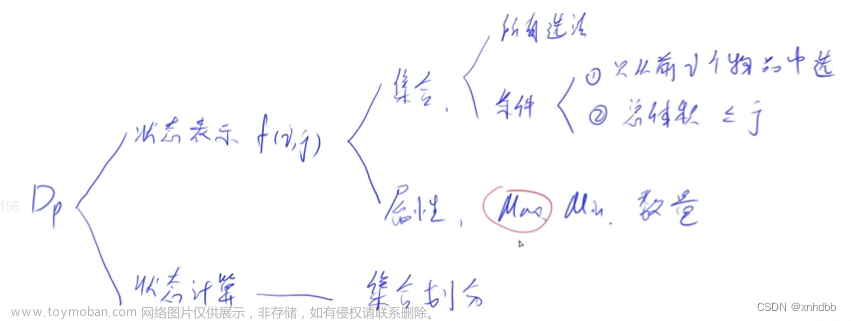
动态规划是一种作者认为比较牛逼的算法,原因是作者初学时非常困难,认为这玩意非常抽象,它往往在求一些最大,最小XXXX问题上有妙用,这篇文章可以帮大家简单理解一下DP的含义。
对了,这玩意也叫DP,原因是动态规划的英文原意是(dynamic programming)。
然后我们以一个引子来介绍一下
大家可以先独立思考一下这道题目。
题目描述
今有面值为 1、5、11 元的硬币各无限枚。
想要凑出 n 元,问需要的最少硬币数量。
输入格式
仅一行,一个正整数 n。
输出格式
仅一行,一个正整数,表示最少需要的硬币个数。
样例:
输入#1:15
输出#1:3
输入#2:12
输出#2:2
这里附上交题链接:https://www.luogu.com.cn/problem/B3635
———————————————————————————————————————————
这个问题第一眼看到,我觉得大家的做法都是会想到贪心,先拿大的凑,然后再拿小的凑,然后多试几下之后就发现似乎不太对,比如20的话用贪心思路是11+5+1+1+1+1,而实际上5+5+5+5更优。
然后搞半天发现这玩意似乎没啥规律,咋拿都没有一个通用的最优策略,那咋办呢?
别急,我们先细想一下如何凑成某种面值?
假设现在我们要凑一个20,那么我这个20能怎么来呢? 可以轻松得出,从9加个11而来,从15加个5而来,从19加个1而来。
然后我再看9,15,19能咋来,然后再看能到9,15,19的数又是咋来的。。。。子子孙孙无穷尽也。。。。。。
这样想似乎思维难度有些大,不如我们正过来想。
一开始我一分钱没凑,于是我的初始状态就是0。
我们开一个表来方便理解

那我们现在拥有0的状态了,我们可以推一下从0到其他价值。
容易得到,0能去1,5,和11。
于是这个表变成了

然后我们0弄好了,再瞅瞅1能去哪

然后就发现我们能用1再+1变成2,1再+5变成6,1再+11变成12。
再看2能去哪

然后看3

再看4
然后发现4可以+1后到5,但是0可以直接+5到5,我用4到5的话要花费5个硬币,而我0到5只花费1个硬币,用4到5的话不是血亏吗,所以5应该留下那个更小的值,于是表就变成了

从这里开始发现,从前往后看的每个数,都是由前面的数倾尽全力给你的最小的硬币数量,是最优的,那就由此得出猜想,我后面的最优都可以通过前面的最优来算出来,我们继续进行模拟。
5:

6:

6到11发现也是血亏的,不如直接0到11,所以此时价值11最少只需1个币。
7:
8:

9:
10:

这里我们用10更新时发现15这里最优硬币数是5,但我自己凑(10)的硬币数最少只要俩,那我到15只用再加个5块的硬币就够了,于是15应该被优化成3枚硬币。。。。
然后同时我10+11超过20了,后面都是无效更新,那我就不填到表里去了。
后面一直用这个思路:
最后得出这个表

然后发现推20的话,最优是4枚硬币。
推所有的数都是这样,这个表里凑成的所有的价值,都是最优的。。
附上这题的AC代码:
可以用数组模拟这个表格,进行DP。文章来源:https://www.toymoban.com/news/detail-760172.html
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int a[N];
int main()
{
int n; cin>>n;
for(int i=1;i<=n;i++)
{
if(i<5) a[i]=a[i-1]+1;
else if(i>=5 && i<11) a[i]=min (a[i-5]+1 , a[i-1]+1);
else a[i]=min ( a[i-11]+1, min( a[i-5]+1 , a[i-1]+1 ));
}
cout<<a[n]<<" ";
}最后总结一下,我们发现DP的思想,就是用前面的最优解来推后面的最优解,也就是局部最优可以推出全局最优,这也是这个思想抽象的地方,把这题理解透彻后明天听课应该能舒服一些,做完后可以用这种思路做一下其他简单DP题嗷,以便加深理解。文章来源地址https://www.toymoban.com/news/detail-760172.html
到了这里,关于动态规划の入门小题,适合0基础看的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!