数据结构之二叉树与堆以及力扣刷题函数扩展-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构之二叉树与堆以及力扣刷题函数扩展。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

个人主页：点我进入主页

专栏分类：C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶

C语言刷题数据结构初阶

欢迎大家点赞，评论，收藏。

一起努力

1.前言

2.树

2.1概念

2.2树的相关概念

3.堆

3.1堆的概念

3.2小堆函数实现

4.力扣刷题函数

5.总结

1.前言

在前面我们学习了关于顺序表，链表，栈，队列的存储方式。今天我将给大家带来关于树的一些内容以及堆的部分内容，详细包括树的定义，树相关的概念，二叉树和满二叉树的概念，树代码的实现会在后面的内容，大堆和小堆的代码实现。今天的内容相较于前面会有一点难以理解，希望大家可以认真学习，当然还有几个力扣刷题的函数扩展，其中的内容就绝对会让你感到其中的乐趣。

2.树

2.1概念

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。有一个特殊的结点，称为根结点，根节点没有前驱结点除根节点外，其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm，其中每一个集合Ti(1<= i<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继因此，树是递归定义的。

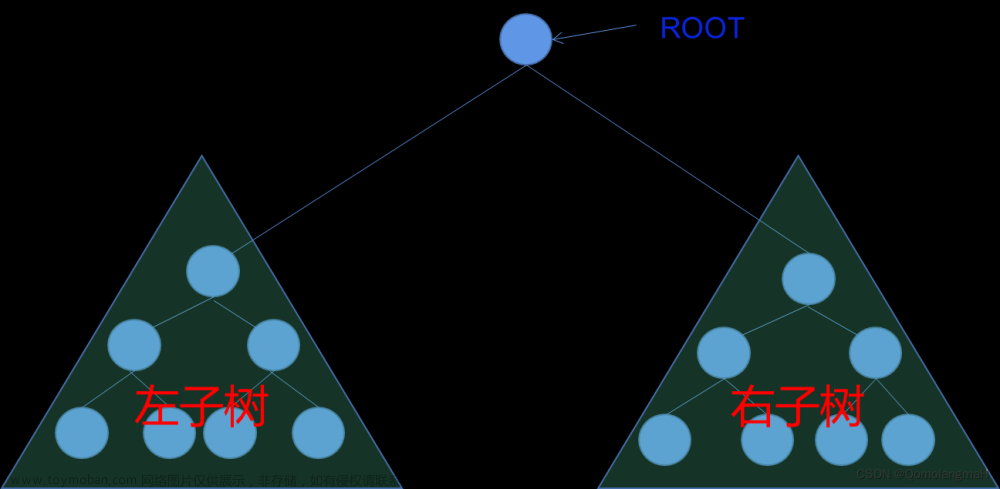
下面我给出关于树的图：

数据结构之二叉树与堆以及力扣刷题函数扩展,数据结构初阶,数据结构

2.2树的相关概念

节点的度：一个节点含有的子树的个数称为该节点的度；如上图：A的为6
叶节点或终端节点：度为0的节点称为叶节点；如上图：B、C、H、I...等节点为叶节点
非终端节点或分支节点：度不为0的节点；如上图：D、E、F、G...等节点为分支节点
双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；如上图：A是B的父节点
孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；如上图：B是A的孩子节点
兄弟节点：具有相同父节点的节点互称为兄弟节点；如上图：B、C是兄弟节点
树的度：一棵树中，最大的节点的度称为树的度；如上图：树的度为6
节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
树的高度或深度：树中节点的最大层次；如上图：树的高度为4
堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点
节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先
子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙
森林：由m（m>0）棵互不相交的树的集合称为森林。

3.堆

3.1堆的概念

如果有一个关键码的集合K = { ，，，…， }，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足： <= 且 <= ( >= 且 >= ) i = 0，1， 2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。堆我们分为大堆个小堆，大堆是父节点永远大于子节点，小堆是父节点永远小于子节点。堆的图我们认为堆是如下的样子：

数据结构之二叉树与堆以及力扣刷题函数扩展,数据结构初阶,数据结构

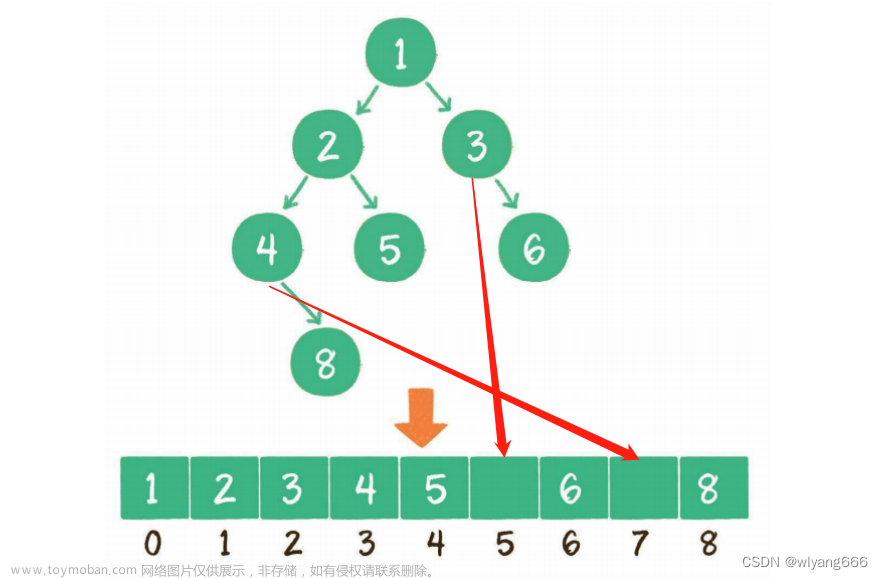
事实上我们是顺序表的形式存储的，我们知道堆是一颗完全二叉树，我们将树的每个节点用数字进行标记，如下:

数据结构之二叉树与堆以及力扣刷题函数扩展,数据结构初阶,数据结构

我们不难得出我们知道父节点的编号为n，左孩子的编号为2n+1,右孩子的编号为2n+2，假设左孩子的标号为n那么父节点的编号为(n-1)/2,我们设右孩子的节点为n那么父节点的编号为(n-1)/2，那我们很容易得到孩子节点编号为n父节点的编号为(n-1)/2，根据这一特点我们就可以利用顺序表进行存储，这样也能更好的找到父节点和孩子节点的位置，接下来我们以实现小堆为例子来展示一下大堆和小堆的实现（大堆和小堆的差距只有向上调整的部分符号不同，其余基本一致）。

3.2小堆函数实现

#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
void Swap(MyHeapData* num1, MyHeapData* num2)
{
	MyHeapData temp = *num1;
	*num1 = *num2;
	*num2 = temp;
}
void AdJustUp(MyHeapData* arr, int size)
{
	assert(arr);
	int child = size - 1, parent = (child - 1) / 2;
	while (child > 0)
	{
		if (arr[child] < arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
			break;
	}
}
void HeapInit(Heap* php)
{
	assert(php);
	php->data = (MyHeapData*)malloc(sizeof(MyHeapData));
	php->size = 0;
	php->capacity = 0;
}
void HeapDestory(Heap* php)
{
	assert(php);
	free(php->data);
	php->data = NULL;
}
void HeapPush(Heap* php, MyHeapData x)
{
	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity + 2;
		MyHeapData* arr = (MyHeapData*)realloc(php->data, newcapacity * sizeof(MyHeapData));
		if (arr == NULL)
		{
			perror("realloc fail");
			return;
		}
		php->data = arr;
		php->capacity = newcapacity;
	}
	php->data[php->size++] = x;
	AdJustUp(php->data, php->size);
}
void print(Heap* php)
{
	for (int i = 0; i < php->size; i++)
		printf("%d ", php->data[i]);
}
void HeapPop(Heap* php)
{
	assert(php);
	if (!HeapEmpty(php))
	{
		Swap(&php->data[0], &php->data[php->size - 1]);
		php->size--;
		AdJustDown(php->data, php->size);
	}
}
void AdJustDown(MyHeapData* arr, int size)
{
	assert(arr);
	int parent = 0, child = parent * 2 + 1;
	while (child<size)
	{
		if (child + 1 < size && arr[child] > arr[child + 1])
		{
			child++;
		}
		Swap(&arr[parent], &arr[child]);
		parent = child;
		child = parent * 2 + 1;
	}
}
bool HeapEmpty(Heap* php)
{
	assert(php);
	return php->size == 0;
}
void text()
{
	Heap ph;
	HeapInit(&ph);
	HeapPush(&ph, 7);
	HeapPush(&ph, 6);
	HeapPush(&ph, 4);
	HeapPush(&ph, 5);
	HeapPush(&ph, 1);
	HeapPush(&ph, 1);
	HeapPush(&ph, 3);
	print(&ph);
	printf("\n");
	HeapPop(&ph);
	print(&ph);
	printf("\n");
	HeapPop(&ph);
	print(&ph);
	HeapDestory(&ph);
}

到这里我们的小堆就实现完了。

4.力扣刷题函数

函数为sscanf函数和sprintf函数，其中sscanf函数是将任意类型数据储存在字符串中，spintf函数是将字符串数据输入到新的变量中，他们重新定义了输入输出流，我们看下面代码来感受一下：

#include<stdio.h>
int main()
{
	int a = 10;
	char arr[] = "abcd";
	double f = 1.99;
	char brr[100];
	sprintf(brr, "%d %s %f", a, arr, f);
	printf("%s\n", brr);
	a = 0;
	double b = 0.0;
	sscanf(brr, "%d %s %f", &a, &arr, &b);
	printf("%d %s %f", a, arr, f);
	return 0;
}

运行结果如下：

数据结构之二叉树与堆以及力扣刷题函数扩展,数据结构初阶,数据结构