对无向图进行邻接矩阵的转化，并且利用DFS（深度优先）和BFS（广度优先）算法进行遍历输出，在邻接矩阵存储结构上，完成最小生成树的操作。-Toy模板网

这篇具有很好参考价值的文章主要介绍了对无向图进行邻接矩阵的转化，并且利用DFS（深度优先）和BFS（广度优先）算法进行遍历输出，在邻接矩阵存储结构上，完成最小生成树的操作。。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一实验目的

二实验内容及要求

实验内容：

实验要求：

三实验过程及运行结果

一算法设计思路

二源程序代码

三、截图

四调试情况、设计技巧及体会

一实验目的

1．掌握图的相关概念。

2．掌握用邻接矩阵和邻接表的方法描述图的存储结构。

3．掌握图的深度优先搜索和广度优先搜索遍历的方法及其计算机的实现。

4．理解最小生成树的有关算法

二实验内容及要求

实验内容：

选择邻接矩阵或邻接链表存储结构，掌握图的创建、遍历、最小生成树、拓扑排序、关键路径、最短路径等典型操作。

编程实现如下功能：

（1）输入无向图的顶点数、边数及各条边的顶点对，建立用邻接矩阵表示的无向图。

（2）对图进行深度优先搜索和广度优先搜索遍历，并分别输出其遍历序列。

（3）在邻接矩阵存储结构上，完成最小生成树的操作。

实验要求：

1.键盘输入数据；

2.屏幕输出运行结果。

3.要求记录实验源代码及运行结果。

4.运行环境：CodeBlocks/Dev c++/VC6.0等C编译环境

三实验过程及运行结果

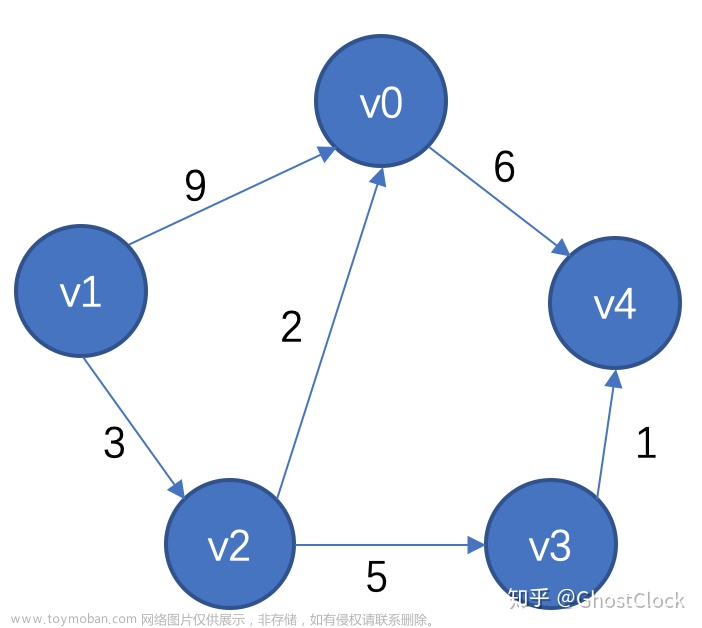
实验一：对无向图进行邻接矩阵的转化，并且利用DFS和BFS算法进行遍历输出，在邻接矩阵存储结构上，完成最小生成树的操作。

一算法设计思路

包含七个功能函数和一个主函数：void initialMatrix(Graph *g,int n)、void CreatMatrix(Graph *g,int startPoint,int endPoint)、void InputEdge(Graph* g, int n)、void OutputMatrix(Graph g,int n)、void DFSTravers(Graph &g,int i)、void BFSTraverse(Graph &g)、void primMST(Graph* graph)

void initialMatrix(Graph *g,int n)：这个函数是一个用于初始化图的邻接矩阵的函数。使用两个嵌套的循环遍历邻接矩阵的每个元素。在每次循环中，将矩阵中的元素赋值为 0，表示该位置上的边不存在。在外层循环中，将图结构中的顶点数组 g->vex 的每个元素赋值为 1，表示该顶点存在。

void CreatMatrix(Graph *g,int startPoint,int endPoint)：这段函数是一个用于创建图的邻接矩阵的函数。将邻接矩阵中起始顶点 startPoint 和结束顶点 endPoint 所对应的位置的元素赋值为它们之间的绝对值差，即 abs(startPoint - endPoint)。这个值可以表示边的权值或距离。由于是无向图，所以将邻接矩阵中结束顶点 endPoint 和起始顶点 startPoint 所对应的位置的元素也赋值为相同的绝对值差。将图结构中的边数 g->numEdges 加一，表示添加了一条新的边。

void InputEdge(Graph* g, int n)：这段函数是用于输入图的边并创建邻接矩阵的函数声明两个整型变量 startPoint 和 endPoint，用于存储输入的边的起始顶点和结束顶点。使用一个循环，循环次数为边的数量 n。在每次循环中，通过输入操作获取用户输入的起始顶点和结束顶点，分别存储到 startPoint 和 endPoint 变量中。调用 CreatMatrix 函数，将起始顶点和结束顶点作为参数传递给 CreatMatrix 函数，并将它们减去 1，以适应数组从 0 开始的索引。CreatMatrix 函数会根据传入的起始顶点和结束顶点，在邻接矩阵中设置相应的边。

void OutputMatrix(Graph g,int n)：这段函数是用于输出图的邻接矩阵的函数输出一行提示信息，告诉用户接下来要输出图的邻接矩阵。使用两个嵌套的循环，外层循环控制行数，内层循环控制列数，循环次数均为图的顶点数量 n。在每次循环中，通过cout 语句输出图结构中邻接矩阵的第 i 行第 j 列的元素，即 g.matrix[i][j]。在每行输出完毕后，通过cout 语句输出换行符 \n，使下一行的输出从新的一行开始。

void DFSTravers(Graph &g,int i)：这段函数是用于实现深度优先搜索（DFS）遍历图的函数。

首先判断顶点表中下标为 i 的顶点是否已经被遍历，通过检查 g.vex[i] 的值是否为 1 来判断。如果顶点未被遍历，则将 g.vex[i] 的值赋为 0，表示该顶点已被遍历。使用一个循环，循环次数为图的顶点数量 g.numVertices。在每次循环中，判断从顶点 i 到顶点 j 是否存在边，通过检查 g.matrix[i][j] 的值是否大于 0 来判断。如果存在边，则递归调用 DFSTravers 函数，以顶点 j 作为新的起始顶点，继续深度优先搜索遍历。在遍历完所有与顶点 i 相邻的顶点后，通过 cout 语句输出顶点 i 的值加 1，表示遍历到了顶点 i。由于 DFS 是递归的过程，所以在遍历完当前顶点后，会回溯到上一个顶点，继续遍历下一个未被遍历的相邻顶点。

void BFSTraverse(Graph &g)：这段函数是用于实现广度优先搜索（BFS）遍历图的函数。

声明一个数组 a 用于模拟队列，初始化为全零。

声明两个计数器变量 countA 和 count，分别用于记录遍历次数和队列的索引。

声明一个标志变量 flag，用于判断某个顶点是否已经出现过。

使用一个外层循环，循环条件为 countA < g.numVertices-1，即直到遍历完所有顶点。

在每次循环中，使用一个内层循环，循环次数为图的顶点数量 g.numVertices。

在内层循环中，首先判断从队列中当前索引位置 a[count] 到顶点 j 是否存在边，通过 g.matrix[a[count]][j] 的值是否大于 0 来判断。

如果存在边，则使用一个额外的循环遍历队列 a，判断顶点 j 是否已经在队列中出现过。

如果顶点 j 之前未出现过，则将其添加到队列中，即 a[++countA] = j。

在遍历完当前顶点的所有相邻顶点后，将 count 自增，继续下一轮循环。循环结束后，使用一个循环输出队列 a 中的顶点，表示广度优先搜索的遍历顺序。

void primMST(Graph* graph)：这个函数用于实现 Prim 算法求解最小生成树的函数

首先声明并初始化一些辅助数组和变量，包括 selected 数组用于标记顶点是否被选择，parent 数组用于记录顶点的父节点，minWeight 数组用于记录顶点到最小生成树的边的权重，totalWeight 变量用于记录最小生成树的总权重。

然后初始化 minWeight 数组，将所有顶点的初始权重设为无穷大（INT_MAX），表示初始状态下都不与最小生成树相连。

接着将起始顶点的权重设为 0，表示该顶点为最小生成树的起点。

然后使用一个循环，循环次数为图的顶点数量减 1（因为最小生成树有 n-1 条边）。在每次循环中，找到权重最小的未选择顶点（即 minWeight 数组中最小的值），记录其索引为 minIndex。将该顶点标记为已选择，并将其权重加到 totalWeight 中。遍历所有未选择的顶点，如果存在一条边连接到该顶点且权重小于该顶点的当前最小权重，则更新该顶点的父节点为 minIndex，并更新其最小权重为边的权重。

循环结束后，输出最小生成树的边和总权重。

二源程序代码

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <iostream>

using namespace std;
/*对无向图进行邻接矩阵的转化，并且利用DFS和BFS算法进行遍历输出，
在邻接矩阵存储结构上，完成最小生成树的操作。*/
#define MAX_VERTICES 100
typedef struct Graph
{
	int vex[MAX_VERTICES] = { 0 };//顶点表 0为初始值，没这个顶点
	    int matrix[MAX_VERTICES][MAX_VERTICES];//邻接矩阵
	    int numVertices;//顶点数
	    int numEdges;//边数
	} Graph;
void initialMatrix(Graph *g,int n)//初始化矩阵，赋值为0
{
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			g->matrix[i][j] = 0;//数组从0开始
		}
		g->vex[i] = 1;//1代表有这个顶点
	}
}
void CreatMatrix(Graph *g,int startPoint,int endPoint)//创建邻接矩阵
{
	g->matrix[startPoint][endPoint] = abs(startPoint-endPoint);
	g->matrix[endPoint][startPoint] = abs(startPoint-endPoint);//权值
	g->numEdges++;
}
void InputEdge(Graph* g, int n)//输入相应边
{
	int startPoint, endPoint;
	for (int i = 0; i < n; i++)
	{
		cin >> startPoint;
		cin >> endPoint;
		CreatMatrix(g, startPoint-1, endPoint-1);
	}
	
}

void OutputMatrix(Graph g,int n)//输出邻接矩阵
{
	cout << "以下是图的邻接矩阵" << endl;
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
				cout << g.matrix[i][j]<<" ";
		}
			cout << "\n";
	}
}

void DFSTravers(Graph &g,int i)//从下标为0的点开始遍历
{
	//先从第一个点开始遍历，向任意一个方向进行遍历
	//遍历一个节点后将顶点表赋值为已遍历
	//如果遍历后的顶点无后续未遍历的顶点则输出，然后退回到上一个节点
	//由上一个节点的另外一个下一个节点开始遍历依次递归
	if (g.vex[i] == 1)//说明此点未被遍历
	{
		
		g.vex[i] = 0;
		for (int j = 0; j < g.numVertices; j++)//从0结点向后遍历
		{
			if (g.matrix[i][j] >0)
			{
				DFSTravers(g, j);
			}
		}
		cout << i+1<< " ";
	}
}
void BFSTraverse(Graph &g)
{
	//从第一个节点往下，一层一层遍历，从左往右
	//一个节点遍历之后，立刻输出置为已访问
	//剩下的节点再遍历到之前的节点时就已访问，然后不影响操作路径
	int a[MAX_VERTICES] = { 0 };//数组模拟队列
	int countA = 0; int count = 0;
		int flag = 0;
		for (int i=a[count]; countA < g.numVertices-1;i=a[count] )//countA代表循环次数
		{
			for (int j = 0; j < g.numVertices; j++)
			{
				if (g.matrix[a[count]][j] >0)
				{
					for (int k = 0; k < g.numVertices; k++)
					{
						if (a[k] == j)
						{
							flag = 1;//代表之前已出现过这个点
							flag = 2;
							break;
						}
					}
					if (flag == 0)
					{
						a[++countA] = j;
						
					}
					if (flag == 2)
						flag = 0;
				}
			}
			count++;
		}
		for (int i = 0; i < g.numVertices; i++)
			cout << a[i] +1<< " ";

}


void primMST(Graph* graph) {
	int selected[MAX_VERTICES];
	int parent[MAX_VERTICES];
	int minWeight[MAX_VERTICES];
	int totalWeight = 0;

	for (int i = 0; i < graph->numVertices; i++) {
		selected[i] = 0;
		parent[i] = -1;
		minWeight[i] = INT_MAX;
	}

	minWeight[0] = 1;

	for (int count = 0; count < graph->numVertices - 1; count++) {
		int minIndex = -1;
		int min = INT_MAX;

		for (int i = 0; i < graph->numVertices; i++) {
			if (!selected[i] && minWeight[i] < min) {
				min = minWeight[i];
				minIndex = i;
			}
		}

		selected[minIndex] = 1;
		totalWeight += min;

		for (int i = 0; i < graph->numVertices; i++) {
			if (graph->matrix[minIndex][i] && !selected[i] && graph->matrix[minIndex][i] < minWeight[i]) {
				parent[i] = minIndex;
				minWeight[i] = graph->matrix[minIndex][i];
			}
		}
	}

	printf("\n最小生成树边缘：\n");
	for (int i = 1; i < graph->numVertices; i++) {
		printf("%d - %d\n", parent[i]+1, i+1);
	}
	printf("总重量： %d\n", totalWeight);
}

int main()
{
	Graph g;
	int n;
	cout << "请输入图中的顶点个数" << endl;
	cin >> n;
	g.numVertices = n;
	initialMatrix(&g,n);
	cout << "请输入边的条数和组成边的顶点" << endl;
	int numEdges;
	cin >> numEdges;
	InputEdge(&g,numEdges);
	OutputMatrix(g, n);
	
	cout << "深度优先搜索遍历的结果为：" << endl;
	DFSTravers(g, 0);
	cout << "\n广度优先搜索遍历的结果为：" << endl;
	BFSTraverse(g);

	primMST(&g);
	


	return 0;
}

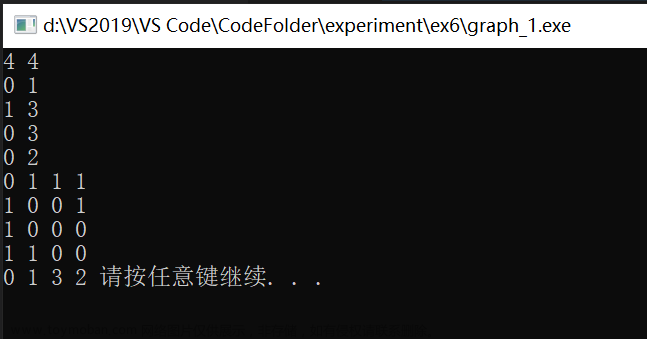
三、截图

对无向图进行邻接矩阵的转化，并且利用DFS（深度优先）和BFS（广度优先）算法进行遍历输出，在邻接矩阵存储结构上，完成最小生成树的操作。,数据结构及算法,算法入门,数据结构,算法,深度优先,宽度优先,c语言,数据结构

四调试情况、设计技巧及体会

本次实验涉及到了建立无向图的邻接矩阵表示、深度优先搜索和广度优先搜索遍历以及最小生成树的操作。通过完成这些实验内容，我积累了一些宝贵的经验和技巧，并且也遇到了一些典型的错误。以下是我对实验过程中的错误及修改方法的总结，以及我从本次实验中学到的技巧和经验。

实验过程中出现的典型错误及修改方法：

（1）邻接矩阵的初始化有误，导致后续操作出现问题

解决方法：对邻接矩阵的初始化进行仔细检查，确保每个元素都被正确地初始化。

（2）错误：在深度优先搜索或广度优先搜索遍历时，循环条件或循环变量设置错误。

修改方法：仔细检查循环条件和循环变量的设置，确保循环能够正确遍历图的所有顶点。注意边界条件和循环变量的更新。

（3）错误：最小生成树操作中，算法实现错误或遗漏了某些边的处理。

修改方法：仔细阅读最小生成树算法的实现逻辑，确保每一步都按照算法的要求进行操作。特别是在选择最小权重边和更新顶点权重时，要仔细检查条件和操作是否正确。

2. 学到的技巧和积累的经验。

（1）在邻接矩阵的创建过程中，我最初没有正确理解邻接矩阵的特性，导致了矩阵的构建错误。具体来说，我在构建邻接矩阵时，没有正确地处理顶点之间的双向连接关系。在修正后，我明白了在邻接矩阵中，如果顶点i与顶点j之间存在一条边，那么矩阵的第i行和第j列上的元素值应为1，而其他位置的元素值应为0。

（2）在进行深度优先搜索时，我首先需要理解了它的基本原理：从图的某个起始顶点开始，沿着一条路径一直到达最深的顶点，然后回溯到之前的节点，继续探索下一条路径。在这个过程中，我犯了一个错误，那就是在访问了某个顶点后没有正确地回溯。修正这个错误后，我明白了在进行深度优先搜索时，必须正确处理访问和未访问的顶点状态，才能确保遍历的正确性。

在实现广度优先搜索时，我遇到的问题是如何正确地访问每一层的顶点。修正的方法是明白在广度优先搜索中，需要使用一个队列来存储每一层的顶点，并且需要正确处理队列的入队和出队操作。

（3）在进行Prim算法实验时，我遇到的主要问题是如何正确地找到最小边以及如何正确地将新顶点加入生成树中。修正的方法是理解并实现了一个优先队列来存储边，并按照边的权重进行排序。同时，我也学会了如何正确地更新生成树中的顶点和边。文章来源地址https://www.toymoban.com/news/detail-761045.html

到了这里，关于对无向图进行邻接矩阵的转化，并且利用DFS（深度优先）和BFS（广度优先）算法进行遍历输出，在邻接矩阵存储结构上，完成最小生成树的操作。的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！