【数据结构】二叉树的创建和遍历（先序、中序、后序）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】二叉树的创建和遍历（先序、中序、后序）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

最近一段时间学习了数据结构中二叉树的基本操作，包括二叉树的结构、二叉树的创建、递归先序中序后序遍历、非递归遍历等，想着把二叉树的相关知识和自己的见解放到网上来让网友看看是否正确，想和网友一起共同交流。

先了解一下二叉树的三个基本性质：

性质1：在非空二叉树中，第i层上至多有2i-1个结点(i≧1)。

性质2：深度为k的二叉树至多有2k-1个结点（k≧1) 。

性质3：对任何一棵二叉树，若其叶子结点数为n0，度为2的结点数为n2，则n0=n2+1。

二叉树的存储也是有两种方式：顺序存储和链式存储。

这里给出链式存储的定义：包括一个数据域、一个左孩子、一个右孩子。

typedef int TElemType;
typedef struct BiTNode{
	TElemType data;
	struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

要创建一个二叉树，可以通过先序遍历创建二叉树的方法：

大体过程为：

输入根结点，判断是否为-1（空），若为-1，则二叉树为空，否则不为空。
为其动态内存分配空间，输入左子节点，因为是先序遍历创建，要遵循根、左、右的顺序，所以对左子节点再递归调用该函数直到NULL。
再输入右子节点，同理，用相同的方法对右子节点递归调用该函数直到NULL。

代码如下：

void createBiTree(BiTree *t)
{
	//先序遍历创建二叉树 
	int e;
	scanf("%d",&e);
	if(e==-1)
		*t=NULL;//二叉树为空
	else
	{
		*t=(BiTree)malloc(sizeof(BiTNode));//动态内存分配
		(*t)->data=e;
		printf("请输入%d的左子节点的值：",e);
		createBiTree(&(*t)->lchild);
		printf("请输入%d的右子节点的值：",e);
		createBiTree(&(*t)->rchild);
	}
}

创建好一个二叉树后，就要对他进行遍历。

先序遍历：

递归：若二叉树为空，则遍历结束；否则

⑴ 访问根结点；⑵ 先序遍历左子树(递归调用本算法)；⑶ 先序遍历右子树(递归调用本算法)。

非递归：若二叉树为空，则返回；否则，令p=T；⑴ 访问p所指向的结点；⑵ q=p->Rchild ，若q不为空，则q进栈；⑶ p=p->Lchild ，若p不为空，转(1)，否则转(4)；⑷ 退栈到p ，转(1)，直到栈空为止。

中序遍历：

递归：若二叉树为空，则遍历结束；否则⑴ 中序遍历左子树(递归调用本算法)；⑵ 访问根结点；⑶ 中序遍历右子树(递归调用本算法)。

非递归：

若二叉树为空，则返回；否则，令p=T⑴ 若p不为空，p进栈， p=p->Lchild ；⑵ 否则(即p为空)，退栈到p，访问p所指向的结点；⑶ p=p->Rchild ，转(1)；直到栈空为止。

后序遍历：

递归：若二叉树为空，则遍历结束；否则⑴ 后序遍历左子树(递归调用本算法)；⑵ 后序遍历右子树(递归调用本算法) ；⑶ 访问根结点。

非递归：若二叉树为空，则返回；否则，令p=T；⑴ 第一次经过根结点p，不访问；p进栈S1 ， tag 赋值0，进栈S2，p=p->Lchild 。⑵ 若p不为空，转(1)，否则，取状态标志值tag ： ⑶ 若tag=0：对栈S1，不访问，不出栈；修改S2栈顶元素值(tag赋值1) ，取S1栈顶元素的右子树，即p=S1[top]->Rchild ，转(1)；⑷ 若tag=1：S1退栈，访问该结点；

直到栈空为止。

递归先序遍历的代码如下：

void PreOrderTraverse(BiTree t)
{
	//递归先序遍历 
	if(t!=NULL)
	{
		printf("%d",t->data);
		PreOrderTraverse(t->lchild);
		PreOrderTraverse(t->rchild);
	}
}

递归中序遍历的代码如下：

void InOrderTraverse(BiTree t)
{
	//递归中序遍历 
	if(t!=NULL)
	{
		InOrderTraverse(t->lchild);
		printf("%d",t->data);
		InOrderTraverse(t->rchild);
	}
}

递归后序遍历的代码如下：

void PostOrderTraverse(BiTree t)
{
	//递归后序遍历
	if(t!=NULL)
	{
		PostOrderTraverse(t->lchild);
		PostOrderTraverse(t->rchild);
		printf("%d",t->data);
	} 
}

整体过程就是这样，要想实际测试，完整代码如下：

#include<stdio.h>
#include<stdlib.h>
#define MAXSIZE 200
typedef int TElemType;
typedef struct BiTNode{
	TElemType data;
	struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
void createBiTree(BiTree *t)
{
	//先序遍历创建二叉树 
	int e;
	scanf("%d",&e);
	if(e==-1)
		*t=NULL;
	else
	{
		*t=(BiTree)malloc(sizeof(BiTNode));
		(*t)->data=e;
		printf("请输入%d的左子节点的值：",e);
		createBiTree(&(*t)->lchild);
		printf("请输入%d的右子节点的值：",e);
		createBiTree(&(*t)->rchild);
	}
}
void PreOrderTraverse(BiTree t)
{
	//递归先序遍历 
	if(t!=NULL)
	{
		printf("%d",t->data);
		PreOrderTraverse(t->lchild);
		PreOrderTraverse(t->rchild);
	}
}
void InOrderTraverse(BiTree t)
{
	//递归中序遍历 
	if(t!=NULL)
	{
		InOrderTraverse(t->lchild);
		printf("%d",t->data);
		InOrderTraverse(t->rchild);
	}
}
void PostOrderTraverse(BiTree t)
{
	//递归后序遍历
	if(t!=NULL)
	{
		PostOrderTraverse(t->lchild);
		PostOrderTraverse(t->rchild);
		printf("%d",t->data);
	} 
}
void aPreOrderTraverse(BiTree t)
{
	//非递归先序遍历
	BiTree stack[MAXSIZE];
	int top=0;
	if(t==NULL)
		return;
	BiTree p=t;
	while(!(p==NULL&&top==0))
	{
		while(p)
		{
			printf("%d",p->data);//先访问根结点 
			stack[top]=p;//将p入栈 
			top++;
			p=p->lchild;//p指向左孩子 
		}
		if(top<=0)return;
		else
		{
			top--;
			p=stack[top];
			p=p->rchild;//p指向右孩子 
		}	
	} 
}
int main()
{
	BiTree t;
	printf("请输入根节点的值：");
	createBiTree(&t);
	printf("递归先序遍历二叉树为：");
	PreOrderTraverse(t);
	printf("\n");
	printf("递归中序遍历二叉树为：");
	InOrderTraverse(t);
	printf("\n");
	printf("递归后序遍历二叉树为：");
	PostOrderTraverse(t);
	printf("\n"); 
	printf("非递归先序遍历二叉树为：");
	aPreOrderTraverse(t);
	printf("\n");
}

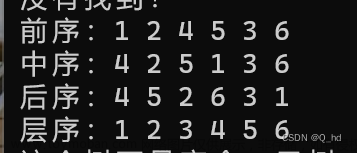
测试结果如下：

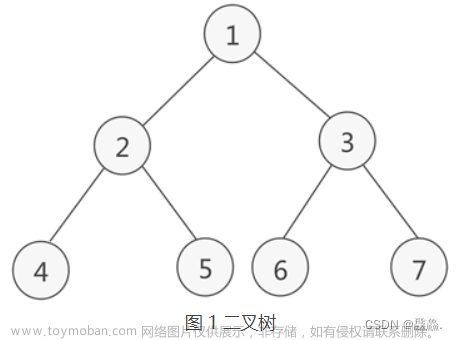
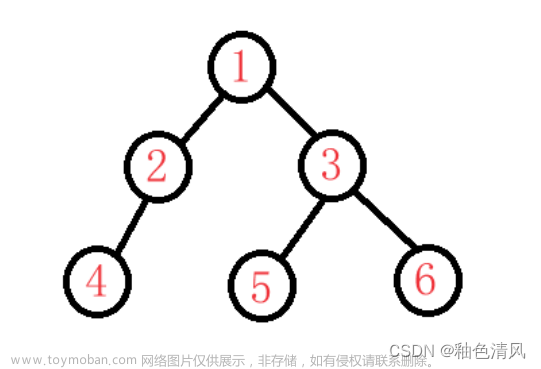
测试的二叉树为：

二叉树的创建与遍历,从文件读取数据建立二叉树,进行该树的先根、后根和中根递归与,数据结构,数据结构,算法