3D Gaussian Splatting学习记录11.2-Toy模板网

这篇具有很好参考价值的文章主要介绍了3D Gaussian Splatting学习记录11.2。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

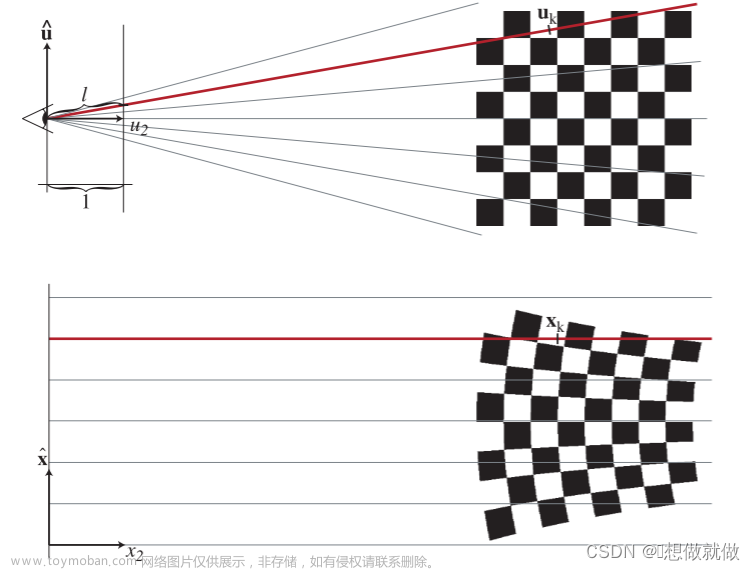
训练结果可视化的尝试

cmd输入以下命令，开始训练

python train.py -s ./dataset/db/drjohnson -m ./dataset/db/drjohnson/output

整个训练（30,000步）大约需要20分钟，但7000步后会保存一个中间模型，效果已经很不错了。训练结束后得到output文件
在Ubuntu 22.04上，运行以下命令来构建可视化工具:

# Dependencies
sudo apt install -y libglew-dev libassimp-dev libboost-all-dev libgtk-3-dev libopencv-dev libglfw3-dev libavdevice-dev libavcodec-dev libeigen3-dev libxxf86vm-dev libembree-dev
# Project setup
cd SIBR_viewers
cmake -Bbuild . -DCMAKE_BUILD_TYPE=Release # add -G Ninja to build faster
cmake --build build -j24 --target install

安装后，找到SIBR_gaussianViewer_app二进制文件，并以模型的路径作为参数运行它:

SIBR_gaussianViewer_app -m ./dataset/db/drjohnson/output

代码细节

参考AI葵的代码讲解

cuda_rasterizer文件夹中，forward.cu文件的preprocessCUDA函数

（1）计算投影出来的半径圆心等，把椭圆近似成圆；

line200，将3D点的矩阵投影；

	// Transform point by projecting
	float3 p_orig = { orig_points[3 * idx], orig_points[3 * idx + 1], orig_points[3 * idx + 2] };
	float4 p_hom = transformPoint4x4(p_orig, projmatrix);
	float p_w = 1.0f / (p_hom.w + 0.0000001f);
	float3 p_proj = { p_hom.x * p_w, p_hom.y * p_w, p_hom.z * p_w };

line215，计算椭球投影成椭圆的样子，用对称2D矩阵记录abbc；

	// Compute 2D screen-space covariance matrix
	float3 cov = computeCov2D(p_orig, focal_x, focal_y, tan_fovx, tan_fovy, cov3D, viewmatrix);

line229，求矩阵特征值，解出椭圆的半径，取长轴的半径；

	float mid = 0.5f * (cov.x + cov.z);
	float lambda1 = mid + sqrt(max(0.1f, mid * mid - det));
	float lambda2 = mid - sqrt(max(0.1f, mid * mid - det));
	float my_radius = ceil(3.f * sqrt(max(lambda1, lambda2)));

line243，计算每个高斯的颜色

	// If colors have been precomputed, use them, otherwise convert
	// spherical harmonics coefficients to RGB color.
	if (colors_precomp == nullptr)
	{
		glm::vec3 result = computeColorFromSH(idx, D, M, (glm::vec3*)orig_points, *cam_pos, shs, clamped);
		rgb[idx * C + 0] = result.x;
		rgb[idx * C + 1] = result.y;
		rgb[idx * C + 2] = result.z;
	}

（2）计算圆所覆盖的像素，即高斯对颜色的贡献。一种加速的方式是，将整张图片分割成很多16*16的小格子，将与圆有交集的格子近似；

line235，getRect函数计算圆覆盖了哪些tile

	getRect(point_image, my_radius, rect_min, rect_max, grid);

line249，保存各个值，其中tilesTouch存储了所覆盖的tile

	// Store some useful helper data for the next steps.
	depths[idx] = p_view.z;
	radii[idx] = my_radius;
	points_xy_image[idx] = point_image;
	// Inverse 2D covariance and opacity neatly pack into one float4
	conic_opacity[idx] = { conic.x, conic.y, conic.z, opacities[idx] };
	tiles_touched[idx] = (rect_max.y - rect_min.y) * (rect_max.x - rect_min.x);

（3）计算每个Gaussian的前后顺序（深度），还有alpha blending；

排顺序，tile（32位的编号）+gaussian（32位）

cuda_rasterizer文件夹中，forward.cu文件的renderCUDA函数

（4）计算每个像素的颜色文章来源地址https://www.toymoban.com/news/detail-761956.html

line263，把每个tile当做一个block，每一个block里的thread就是tile的pixel

// Main rasterization method. Collaboratively works on one tile per
// block, each thread treats one pixel. Alternates between fetching 
// and rasterizing data.
template <uint32_t CHANNELS>
__global__ void __launch_bounds__(BLOCK_X * BLOCK_Y)
renderCUDA(
	const uint2* __restrict__ ranges,
	const uint32_t* __restrict__ point_list,
	int W, int H,
	const float2* __restrict__ points_xy_image,
	const float* __restrict__ features,
	const float4* __restrict__ conic_opacity,
	float* __restrict__ final_T,
	uint32_t* __restrict__ n_contrib,
	const float* __restrict__ bg_color,
	float* __restrict__ out_color)

line295，存在共享内存里，读取一次就好

	// Allocate storage for batches of collectively fetched data.
	__shared__ int collected_id[BLOCK_SIZE];
	__shared__ float2 collected_xy[BLOCK_SIZE];
	__shared__ float4 collected_conic_opacity[BLOCK_SIZE];

line300，T是透过率，穿过越多gaussian就越小，小到一定程度就提前终止，contributor记录经过了多少gaussian

	// Initialize helper variables
	float T = 1.0f;
	uint32_t contributor = 0;
	uint32_t last_contributor = 0;
	float C[CHANNELS] = { 0 };

line333，d是gaussian到中心的距离，power计算点在gaussian分布的概率

			// Resample using conic matrix (cf. "Surface 
			// Splatting" by Zwicker et al., 2001)
			float2 xy = collected_xy[j];
			float2 d = { xy.x - pixf.x, xy.y - pixf.y };
			float4 con_o = collected_conic_opacity[j];
			float power = -0.5f * (con_o.x * d.x * d.x + con_o.z * d.y * d.y) - con_o.y * d.x * d.y;
			if (power > 0.0f)
				continue;

line343，透明度随着概率的减小而减小

			// Eq. (2) from 3D Gaussian splatting paper.
			// Obtain alpha by multiplying with Gaussian opacity
			// and its exponential falloff from mean.
			// Avoid numerical instabilities (see paper appendix). 
			float alpha = min(0.99f, con_o.w * exp(power));
			if (alpha < 1.0f / 255.0f)
				continue;
			float test_T = T * (1 - alpha);
			if (test_T < 0.0001f)
			{
				done = true;
				continue;
			}

到了这里，关于3D Gaussian Splatting学习记录11.2的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！