动态规划背包问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划背包问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

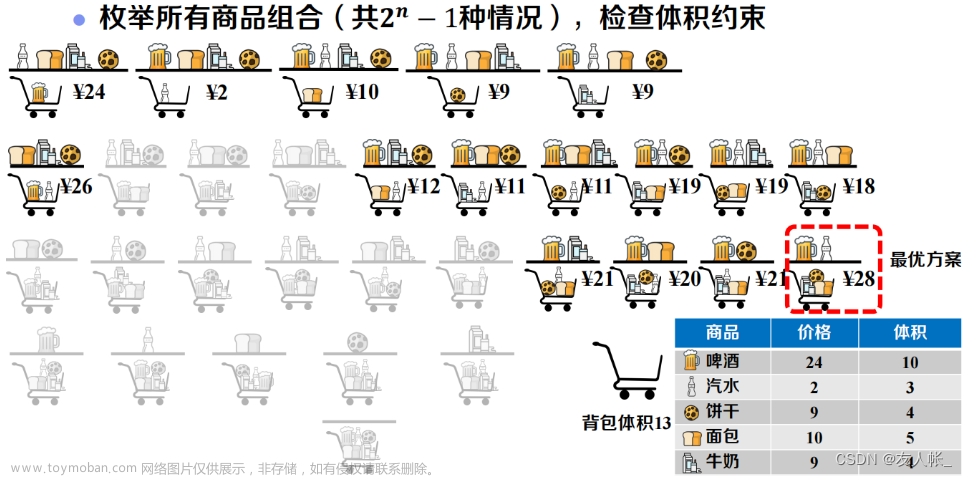
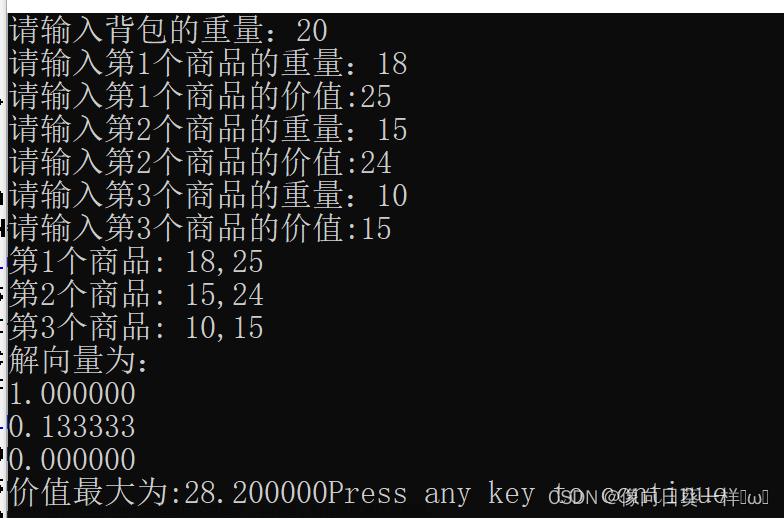
动态规划思想：将一个大问题转化为一个小问题，由小问题的最优解得到大问题的最优解。

1.01背包：

   情景引入：假设有m种物品，每种物品价值分别为value[ i ]，重量分别为weight[ i ]，现在有一个背包，里面最多能装下V大小重量的物品，求问 在不超重的情况下，最多能装下多少价值的物品？

   分析该问题：有m种物品，要拿最多，有同学自然而然的想：“不是往大了拿就行了吗？”这种思想固然可贵，但求得的不一定是最优解，比如背包容量为4，有两种物品，一种重量为1，价值为2，另一种重量为4，价值为7，如果按照贪心思想，每次从7开始拿，那么得到的不是最优解，因为全拿第一种物品更具有性价比（能拿到8价值的物品）

进入正题：

假设有3件物品，每件物品价值分别为value[3] = { 2, 5, 6 } ,重量为 weight[3] = { 1, 3, 4 };背包的最大重量为4，我们列出如下表格：

1 2 3 4
1

对于这个表格，横向表示背包容量，纵向表示能装入该物体和该物体以前物体的最大价值。

对于每一个格子:

选择装入该物体，则空间剩下 j - n[ i ]
不装入该物体，则空间为dp【i - 1 】【 j 】；
然后选择其最大即可，其动态转移方程为:
dp【i】【j】 = max（dp【i-1】【j】，dp【i】【j - n【i】】 + n【i】）；

例子：

[NOIP2005 普及组] 采药

题目描述

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是辰辰，你能完成这个任务吗？

输入格式

第一行有 $2$ 个整数 $T$ （ $\le T \le 1000$ ）和 $M$ （ $\le M \le 100$ ），用一个空格隔开， $T$ 代表总共能够用来采药的时间， $M$ 代表山洞里的草药的数目。

接下来的 $M$ 行每行包括两个在 $1$ 到 $100$ 之间（包括 $1$ 和 $100$ ）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出格式

输出在规定的时间内可以采到的草药的最大总价值。

样例 #1

样例输入 #1

样例输出 #1

提示

【数据范围】

对于 $30\%$ 的数据， $\le 10$ ；
对于全部的数据， $\le 100$ 。

【题目来源】

NOIP 2005 普及组第三题

明显的背包问题，从以上分析可以得到：

AC代码：

#include<iostream>
using namespace std;

const int N=1005;
const int M=105;
int n,m;
int dp[M][N],t[M],v[M];

int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++) cin>>t[i]>>v[i];
	for(int i=1;i<=m;i++)
		for(int j=1;j<=n;j++)
			if(j>=t[i])
				dp[i][j]=max(dp[i-1][j],dp[i-1][j-t[i]]+v[i]);
			else
				dp[i][j]=dp[i-1][j];
	cout<<dp[m][n]<<endl;
	return 0;
}

优化：我们考虑把这个二维数组优化成一维数组：因为我们的思路是从左到右（按照背包的空间大小进行寻找）所以我们同样选定背包的大小作为变量，有以下公式：

dp[ i ] = max(dp[ i ] , dp[ i - weight[ i ]] + value[ i ]);

观察发现，如果外层循环从左到右，则每次调用时总会再次使用前面的值（如调用dp【4】，如果某个条件成立，则在循环中会多次的使用前面的值，这样违背了一种物品只能拿一次的规则，所以我们选择从后面遍历，防止数据被前面破坏：

#include<iostream>
#include<vcruntime_string.h>
#include<algorithm>
using namespace std;

int main()
{
	int t, m;
	int wei[100] = { 0 }, value[1000] = { 0 }, dp[1000] = { 0 };
	cin >> t >> m;

	int i, j;
	for (i = 1; i <= m; i++)
	{
		cin >> wei[i] >> value[i];
	}
	
	for (i = 1; i <= m; i++)
	{
		for (j = t; j > 0; j--)
		{
			if (j >= wei[j])
				dp[j] = max(dp[j], dp[j - wei[i]] + value[i]);
		}
	}
	cout << dp[t];
	return 0;
}

完全背包：

问题描述
辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同种类的草药，采每一种都需要一些时间，每一种也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”
如果你是辰辰，你能完成这个任务吗？
此题和原题（P1048 采药）的不同点：

每种草药可以无限制地疯狂采摘。
药的种类眼花缭乱，采药时间好长好长啊！（暗示数据范围更大）
输入格式
输入第一行有两个整数 T （ 1 ≤ T ≤ 100000 ） T（1 ≤ T ≤ 100000）T（1≤T≤100000） 和 M （ 1 ≤ M ≤ 10000 ） M（1 ≤ M ≤ 10000）M（1≤M≤10000），用一个空格隔开，T TT 代表总共能够用来采药的时间，M MM 代表山洞里的草药的数目。接下来的M行每行包括两个在 1 到 10000之间（包括 1 和 10000）的整数，分别表示采摘某种草药的时间和这种草药的价值。

输出格式
输出一行，这一行只包含一个整数，表示在规定的时间内，可以采到的草药的最大总价值。

样例输入
70 3
71 100
69 1
1 2

样例输出
140

从01背包分析可知，如果可以取得多次
那么有下面公式：(二维的自己推导，和上面的基本一样但是改了一个)

dp[ i ] = max(dp[ i ] , dp[ i - weight[ i ]] + value[ i ]);

从左到右遍历，则每次都会调用前面的和的最大值。

#include<iostream>
#include<vcruntime_string.h>
#include<algorithm>
using namespace std;

int main()
{
	int t, m;
	int wei[100] = { 0 }, value[1000] = { 0 }, dp[1000] = { 0 };
	cin >> t >> m;

	int i, j;
	for (i = 1; i <= m; i++)
	{
		cin >> wei[i] >> value[i];
	}
	
	for (i = 1; i <= m; i++)
	{
		for (j = 1; j <= t; j--)
		{
			if (j >= wei[j])
				dp[j] = max(dp[j], dp[j - wei[i]] + value[i]);
		}
	}
	cout << dp[t];
	return 0;
}