OpenCV 笔记(6)：像素间的基本关系——邻域、邻接、通路、连通、距离-Toy模板网

这篇具有很好参考价值的文章主要介绍了OpenCV 笔记(6)：像素间的基本关系——邻域、邻接、通路、连通、距离。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

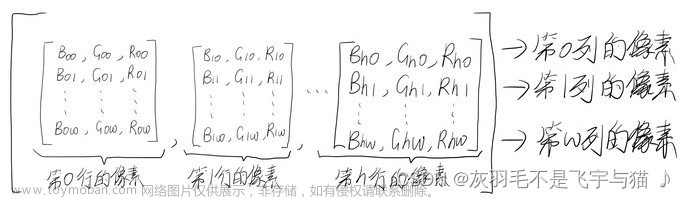
像素是图像的基本元素，像素与像素之间存在着某些联系，理解像素间的基本关系是数字图像处理的基础。常见的像素间的基本关系包括：邻域、邻接、通路、连通、距离。

Part11. 邻域

邻域表示了像素之间的连接关系。

像素(x,y)的邻域，是指与像素(x,y)对应的点的集合{(x+p,y+q)} ，其中 (p,q) 为一对有意义的整数。邻域是像素(x,y)附近像素形成的区域，像素 (x,y) 也被称为中心像素。

最常用的邻域有以下几种：

4 邻域：对于像素(x,y)，上下左右4个像素被称为 4 邻域，使用
表示。4 邻域的四个像素分别是：(x,y-1)、(x,y+1)、(x-1,y)、(x+1,y)。
D 邻域：对于像素(x, y), 其左上、右上、左下、右下的四个对角上的像素组成了 D 邻域，使用
表示。D 邻域四个像素分别是：(x + 1, y + 1)、( x + 1, y - 1)、(x - 1, y + 1)、(x - 1, y - 1)。
8 邻域：对于像素(x,y)，它的4-邻域的点和 D-邻域的点组成了 8 邻域，使用
表示。那么，

比较说明像素邻域,邻接及联通的概念,联系及区别,opencv,笔记,人工智能,计算机视觉

邻域.png

邻域是一个很基础的概念。后续我们对图像进行卷积操作的时候，通常是对当前像素的邻域像素进行操作的。

以一个最简单的均值滤波为例，均值滤波是对于每一个像素点, 将其设定为取其邻域窗口内的所有像素的平均值。

算术均值滤波器的公式：

其中，

表示以像素(x,y)为中心的区域，m*n 是模板的大小。f(x,y) 表示原图像，g(x,y) 表示使用定义的邻域中的像素所计算出的算术平均值。

这里的模板，也可以被称为核(kernels)、窗口(windows)、掩模(mask)。

下图以 3*3 的模板为例，均值滤波会对原图像的每一个像素点，计算它的邻域像素和模版矩阵的对应元素的乘积，然后加起来，作为该像素位置的值。窗口的移动是从左到右，然后从上到下依次移动。

卷积.png

下面，实现一个简单的均值滤波函数

Mat meanFilter(Mat &src, int ksize = 3)
{
    cv::Mat dst = src.clone();

    int k0 = ksize/2;
    int sum[3] = {0,0,0};
    for(int i=k0;i<dst.rows-k0-1;i++)
    {
        for(int j=k0;j<dst.cols-k0-1;j++)
        {
            memset(sum,0, sizeof(sum));

            for(int channel = 0; channel<3; channel++)
            {
                for(int m = 0;m<ksize;m++)
                {
                    for (int n=0;n<ksize;n++)
                    {
                        sum[channel] += src.at<cv::Vec3b>(i-k0+m,j-k0+n)[channel];
                    }
                }

                dst.at<Vec3b>(i,j)[channel] = saturate_cast<uchar>((float)sum[channel] /(ksize*ksize));
            }
        }
    }
    return dst;
}

当然这个代码只是粗略地实现均值滤波，存在着很多优化的空间，例如使用积分图、卷积核分离等。OpenCV 也提供了均值滤波函数 blur() 函数。

int main(int argc,char *argv[])
{
    Mat src = imread(".../flower.jpg");
    imshow("src",src);
    Mat dst;

    dst = meanFilter(src, 15);
    imshow("meanFilter",dst);

    blur(src,dst,Size(15,15));
    imshow("blur",dst);

    waitKey(0);
    return 0;
}

均值滤波函数效果.png

上面只是简单例举了领域的使用场景，后续会有专门的文章来详细介绍卷积和滤波。

Part22. 邻接

邻接是指两个像素，在位置上相邻并且取值相同或相近。

我们用 V 表示定义邻接的灰度值集合。在二值图像中，V={1} 表示值为1的像素邻接。在灰度图像中，V 包含更多的元素。

4 邻接：对于灰度值在 V 集合中的像素 p 和 q，如果 q 在
中，那么像素 p 和 q 是 4 邻接的。
8 邻接：对于灰度值在 V 集合中的像素 p 和 q，如果 q 在
中，那么像素 p 和 q 是 8 邻接的。
m 邻接(混合邻接)：m 邻接是 8 邻接的改进。只要满足以下任何一个条件即可：
- q 在
  中
- q 在
  中，且集合在中没有来自 V 中的像素。

像素 p 和 q 是 4 邻接，那么它们一定是 8 邻接的。反之，不一定成立。

下图反应了 8 邻接会带来二义性。

邻接.png

从图中可以看到，p 是中心像素。

q1、q2 和 p 是 8 邻接的。
q1 和 p 非 m 邻接的。
q2 和 p 是 m 邻接的。

某条通路经过像素 q2、p、q1，那会有几种走法呢？

如果从 p、q1、q2 是 8 邻接的角度看，p 到 q1 可以有2种走法，所以 q2 到 q1 的通路有2条。

同理，从 m 邻接角度看，p 和 q1 只有1种走法，所以 q2 到 q1 的通路只有1条。

所以，m 邻接的引入是为了消除 8 邻接常常带来二义性。

从集合的角度看：

邻接邻接邻接

Part33. 通路

通路：从像素 p

到像素 q 的通路是特定的像素序列，其坐标为：

，，，

并且满足，

和对于是邻接的。

闭合通路：如果满足

，则通路是闭合通路。

由不同的邻接定义，可以得到不同的通路：4 邻接 => 4 通路，8 邻接 => 8 通路，m 邻接 => m 通路

通路.png

所以，从中间的图可以看到 q2 和 q1 之间存在 8 通路，从最右的图可以看到 q2 和 q1 之间存在 m 通路。

从集合的角度看：

通路通路通路

下图中，p-q 通路对应的是不同的通路。

多种通路.png

Part44. 连通

连通：若 S 是图像中的一个像素子集，对于任意的

、

。如果存在一条由 S 中像素组成的从 p 到 q 的通路，则称 p 在图像集 S 中与 q 连通。

邻接是连通的一种特例，连通是由一系列依次邻接的像素组成的。

连通分为 4 连通和 8 连通。

连通分量：对于 S 中任意像素 p，所有与 p 相连通且又在 S 中的像素集合。

连通集：如果 S 中仅有一个连通分量，则 S 称为连通集。

在之前基本图形的绘制那篇文章里，曾介绍过绘图函数所使用的 lineType 参数。

下面对这个参数做一些补充说明：

LINE_4 ：基于 4 连通 Bresenham 算法处理的直线。
LINE_8 ：基于 8 连通 Bresenham 算法处理的直线。
LINE_AA ：基于高斯滤波平滑处理的直线。

lineType 参数.png

下面的例子，展示了使用不同的 lineType 参数的效果

int main(int argc,char *argv[])
{
    Mat image = Mat::zeros(Size(80, 80), CV_8UC3);
    image.setTo(255);// 设置屏幕为白色

    Point p1(20, 0);
    Point p2(80, 60);
    Point p3(0, 0);
    Point p4(80, 80);
    Point p5(0, 20);
    Point p6(60, 80);

    line(image, p1, p2, Scalar(0, 0, 255), 1, LINE_4);
    line(image, p3, p4, Scalar(255, 0, 0), 1, LINE_8);
    line(image, p5, p6, Scalar(0, 255, 0), 1, LINE_AA);

    imshow("src", image);

    waitKey(0);
    return 0;
}

将生成的图片放大，可以看到使用 LINE_4、LINE_8、LINE_AA 画出来的线段效果是不同的。使用 LINE_AA 效果看上去是最好的，其次是 LINE_8。