一、图论基础
图分为有限图与无限图两类,本课只涉及有限图,即顶点和边都是有限集合

(2)有向图:每一条边都是有向的
无向图:每一条边都是无向的
除外都是混合图

注意:有向图边的描述{1.每一条边都需要描述到 2.<始点,终点>
(3)邻接点:两个结点之间有一条边连接它们,它们就是彼此的邻接点
邻接边:连接同一结点的两条边为邻接边
孤立结点:没有任何一条边连接它
零图:仅由孤立结点构成
平凡图:仅由一个孤立结点构成
自回路:边的头和尾连接在同一个节点上
度数:连接结点的边数(一个环算2条边),记为deg(v)

定理(1)图中,所有结点的度数和=2*图中的边数和
(2)度数是奇数的结点的个数必为偶数个

(4)有向图有入度和出度之分:由结点发出的边为出度,接受的结点的边为入度
所有结点的出度数和所有结点的入度数和是一样的,且是边的数目。
结点的出度与入度的和为该结点的度数
(5)平行边:两结点之间有两条边连接,这两条边为平行,可能不止就两条边
拥有平行边的是多重图,不含平行边和环的是简单图
多重图:
简单图:
{完全图:简单图中能够满足每两个结点间都有边
n个结点的无向完全图的边数为:
1/2*n*(n-1)
补图:给定一个图G,由G中所有结点和所有能使G成为完全图的添加边组成的图,称为G的相对于完全图的补图,或简称为G的补图。}
(6)子图:G图中截取的一部分为子图
生成子图:子图中有一部分图拥有所有G图中的结点的称为生成子图
例1. 至少要经过多少次对换才能把6 3 7 8 5 1 2 4 9 10 变为标准
顺序的排列?


K(G):点连通度
λ(G):边连通度
δ(G)
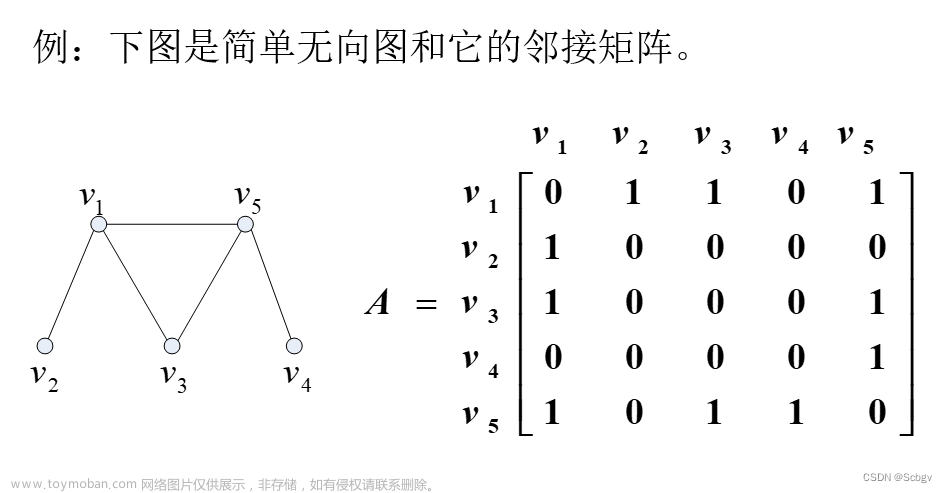
矩阵A是对称矩阵
A^2表示i到j长度为2的路径数目


无向图的权矩阵是对称矩阵

相关的matlab知识:
graph:无向图
G=graph(A):以邻接矩阵A创无向图
G=graph(A,node):使用邻接矩阵A 和顶点nodes创建赋权无向图,其中nodes是表示顶点的字符串。例:nodes=cellstr(strcat('v',int2str([1:6]')));
G=graph:创一个空的无向图
G=graph(s,t):以结点对创无向图
digraph:有向图

G=graph(s,t,weight): 使用顶点对s,t和权重向量创建赋权无向图。
G=graph(s,t,weight,nodes): 使用顶点对s,t和权重向量创建赋权无向图,并使用字符向量
元胞数组nodes指定顶点名称。
W=adjacency(G): 导出图G的邻接矩阵的稀疏矩阵
W=incidence(G): 导出图G的关联矩阵的稀疏矩阵

clc,clear, close all
E=[1,2;1,3; 2,3; 3,2; 3,5; 4,2; 4,6; 5,2; 5,4; 6,5];
s=E(:,1);
t=E(:,2);
nodes=cellstr(strcat('v',int2str([1:6]')));
G=digraph(s,t,[],nodes);
plot(G,'LineWidth',1.5,'Layout','circle')

clc,clear,close all
E=[1,3,10; 1, 4,60; 2, 3, 5; 2, 4, 20; 3, 4, 1];
nodes=cellstr(strcat('v',int2str([1:4]')));
G=graph(E(:,1), E(:,2), E(:,3),nodes);
%% W1=adjacency(G, 'weighted')
nn = numnodes(G);
[s,t] = findedge(G);
W1 = sparse(s,t,G.Edges.Weight,nn,nn)
W2=incidence(G)文章来源:https://www.toymoban.com/news/detail-762111.html
plot(G,'Layout','force','EdgeLabel',G.Edges.Weight)文章来源地址https://www.toymoban.com/news/detail-762111.html
到了这里,关于数学建模——图论学习的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!

![[数学建模]图论之最短路径问题](https://imgs.yssmx.com/Uploads/2024/02/460301-1.png)











