动态规划——完全背包问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划——完全背包问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

写在前面

由于本人实力尚浅，接触算法没多久，写这篇blog仅仅是想要提升自己对算法的理解，如果各位读者发现什么错误，恳请指正，希望和大家一起进步。(●’◡’●)

完全背包问题

了解完全背包问题前可以先去看看01背包问题（良心正解），先了解这个基础问题会更有利于你了解下面的完全背包问题（个人观点）

题目

动态规划——完全背包问题,数据结构与算法,# 动态规划,动态规划,算法,c++,数据结构

思路

重要变量说明：
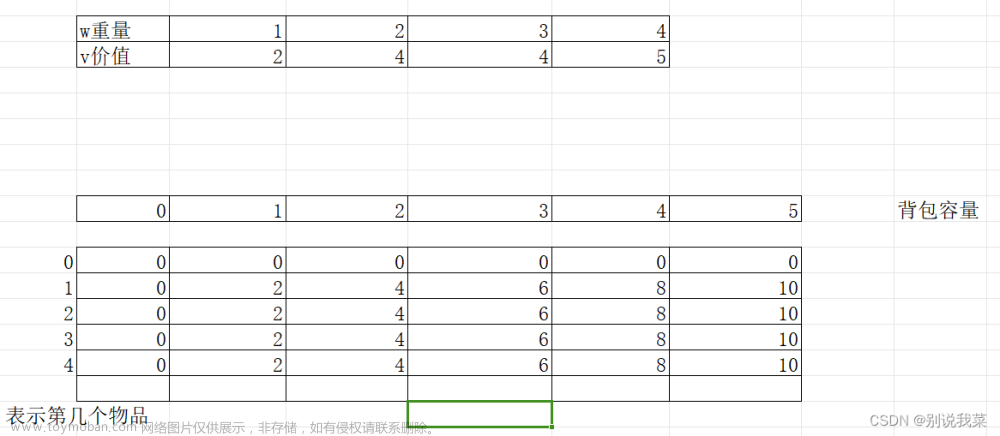
f[][[]:用于状态表示；
w[]：记录每个物品的价值；
v[]：记录每个物品的体积

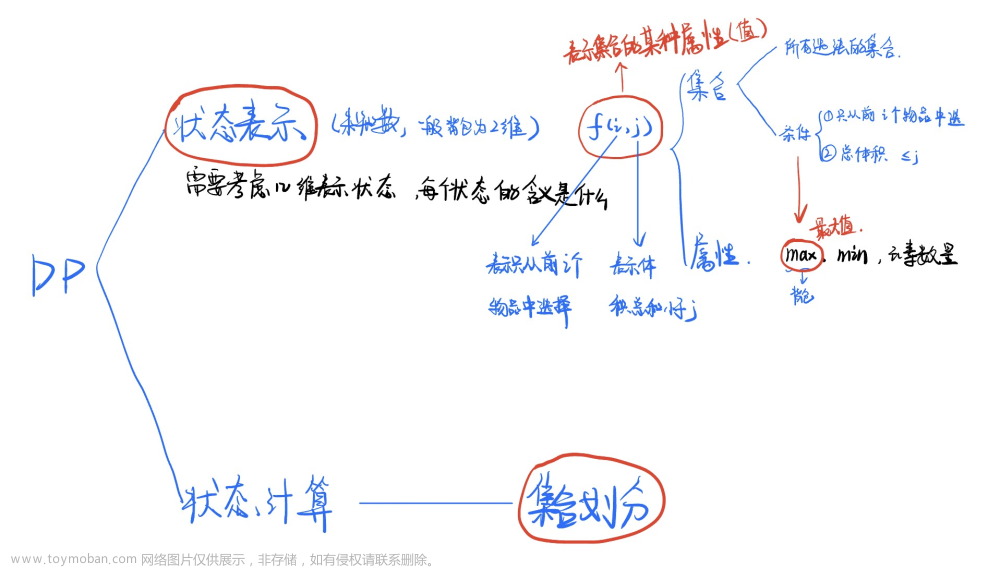
定义二维数组f[][],其中f[i][j]表示在前i个物品，背包容积为j的限制下所能装下的最大价值。这里的f[i][j]就是做法的集合，f[i][j]的值就是最大价值即属性。
从i=1开始枚举，对于第i个物品，都有无数种选择（看似是无数种，其实还是有限制的）：
- 如果不选第i个物品，那么状态转移方程为f[i][j]=f[i-1][j]
- 如果选择第i个物品一次，那么状态转移方程为f[i][j]=f[i-1][j-v[i]]+w[i]
- 如果选择第i个物品二次，那么状态转移方程为f[i][j]=f[i-1][j-2*v[i]]+2*w[i]
- ......
- 如果选择第i个物品k次，那么状态转移方程为f[i][j]=f[i-1][j-k*v[i]]+k*w[i]
我们因为要求最大价值，所以对上面两种情况去max即可

我们发现其实上面的思路大致上和01背包问题差不多，只不过对于每一个物品i，我们不止两种选择（选与不选）而是有无数种选择。所以我们可以在01背包问题的基础上，在两层循环中再套一层循环，表示选择第i个物品多少次。

代码（不优化版，二维数组）

#include<iostream>

using namespace std;
const int N=1010;
int f[N][N],v[N],w[N];

int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d%d",&v[i],&w[i]);
    for(int i=1;i<=n;i++)       //i表示当前选择到第i个物品，我们从第1个物品开始枚举，一直到n个物品
        for(int j=1;j<=m;j++)       //j表示当前背包的容积，我们从1开始枚举，一直到背包的最大的容积
            for(int k=0;k<=j/v[i];k++)      //k表示当前的选择第i个物品的次数，一直到所能选择的最大次数
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
    printf("%d\n",f[n][m]);
    return 0;
}

优化1（降低时间复杂度）

我们可以看到上面的思路虽然可以求解问题，但是时间复杂度是 $O(log_2n)$ ，而题目给出的数据是 $10^3$ ,那么最后就是 $10^9$ ，而我们的要求是1s内，大概是 $10^7-10^8$ 之间，所以我们还要优化

思路

f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w ,  f[i-1,j-2*v]+2*w , f[i-1,j-3*v]+3*w , .....)
f[i , j-v]= max(            f[i-1,j-v]   ,  f[i-1,j-2*v] + w , f[i-1,j-3*v]+2*w , .....)
由上两式，可得出如下递推关系： 
                        f[i][j]=max(f[i,j-v]+w , f[i-1][j])

还是没看懂的宝宝们可以可以看下面这份详细推理
动态规划——完全背包问题,数据结构与算法,# 动态规划,动态规划,算法,c++,数据结构

代码

#include<iostream>

using namespace std;
const int N=1010;
int f[N][N],v[N],w[N];

int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d%d",&v[i],&w[i]);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            {
                if(j>=v[i])
                    f[i][j]=max(f[i-1][j],f[i][j-v[i]]+w[i]);
                else
                    f[i][j]=f[i-1][j];
            }
    printf("%d\n",f[n][m]);
    return 0;
}

思考

我们把完全背包问题和01背包问题做一下对比：
01背包问题：f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);
完全背包问题： f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);
于是乎，聪明的你一定想到了完全背包问题的代码还可以优化，只使用一维数组，降低空间复杂度

优化2（降低空间复杂度）

具体为什么可以只用一维数组请看01背包问题

代码

#include<iostream>

using namespace std;
const int N=1010;
int f[N],v[N],w[N];

int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d%d",&v[i],&w[i]);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            {
                if(j>=v[i])
                    f[j]=max(f[j],f[j-v[i]]+w[i]);
                else
                    f[j]=f[j];
            }
    printf("%d\n",f[m]);
    return 0;
}

再思考

Q：为什么01背包问题使用一维数组时，枚举背包空间时要逆序，而完全背包问题使用一维数组时，枚举背包空间时是正序？
A:01背包问题中我们每次更新用的都应该是上一层即i-1层的数据，但是如果正序枚举背包空间j的话，在更新较大容积时，用到的就是已经污染的数据，即在第i层时，可能在j=v[i]时选了i这个物品，当j=2*v[i]时我们可能又选了i这个物品，而第i这个物品只能被选一次，而逆序枚举时，每次都只可能选择第i这个物品一次。但是在完全背包问题中我们就要用正序，因为我们要的就是已经更新的数据，因为每个物品都有无数个，所以可以选择第i个物品多次

如果你觉得我写题解还不错的，请各位王子公主移步到我的其他题解看看
数据结构与算法部分（还在更新中）：
C++ STL总结 - 基于算法竞赛（强力推荐）
最短路算法——Dijkstra（C++实现）
最短路算法———Bellman_Ford算法（C++实现）
最短路算法———SPFA算法（C++实现）
最小生成树算法———prim算法（C++实现）
最小生成树算法———Kruskal算法（C++实现）
染色法判断二分图（C++实现）
动态规划——01背包问题
Linux部分（还在更新中）：
Linux学习之初识Linux
Linux学习之命令行基础操作