目录
1 标量 scalar
2 向量 /矢量 vector
2.1 什么是向量(直观)
2.2 什么是向量(严格定义)
2.3 向量如何表示?在向量空间的表示方法
3 矩阵(matrix)
3.1 矩阵的定义
3.2 矩阵和向量的关系
3.3 方阵
4 张量(tensor):向量,矩阵都可以看成张量
4.1 张量的定义
4.2 更多维度的张量,举例子
4.3 张量的图形表示
5 具体例子说明 向量,矩阵,张量
5.1 向量
5.2 矩阵
5.3 张量
5.4 常见的写法区别
5.5 一个比较灵活的实际例子
5.5.1 上面这个表直接看成一个5阶张量是没问题的
5.5.2 强行合并一些列,把总列数表为3列
1 标量 scalar
标量 scalar:
- 标量就是一个单独的数!
- 标量还有一种更深刻的说法,就是线性变换时不会发生变化的量.
数有很多种:
- 自然数
- 整数(正负)
- 有理数(包含整数,无限循环小数 or =整数/整数)
- 实数(包含有理数和无理数)
- 复数(包含实数和虚数)
2 向量 /矢量 vector
2.1 什么是向量(直观)
- 向量就是一组数字,而不是一个单个数字,α={x1,x2,x3....xn}
向量vector也叫矢量
- 表示一组n个数构成的有序排列的数
- 向量也可以认为就是 数组list,比如[1,2,3,4,5]
向量的几何表示
- 在各种向量空间里的二维图,三维图里,就是空间里的点(其终点代表了从原点出发的向量)
- 向量,可以认为是带方向的一组数,方向就是 数组里的数字的排序
- 竖着的叫列向量, α={x1,x2,x3....xn}
- 横着的为行向量, αT={x1,x2,x3....xn}
2.2 什么是向量(严格定义)
- 严格定义:在数学中,向量(也称为欧几里得向量、几何向量),指具有大小(magnitude)和方向的量。
- 它可以形象化地表示为带箭头的线段。
- 箭头所指:代表向量的方向;
- 线段长度:代表向量的大小。
- 与向量对应的量叫做数量(物理学中称标量),数量(或标量)只有大小,没有方向。
2.3 向量如何表示?在向量空间的表示方法
- 在一般的向量空间,向量是指从原点出发的一条射线线段
- 线段起点一定是原点,线段终点是向量的内容(x1,x2) 或(x1,x2,x3)或其他,这同时也是向量在这个向量空间的坐标
因此这种向量空间特点是
- 向量空间一定有原点
- 每个向量都是从原点出发的射线线段,用终点坐标即可代表向量
- 不存在2个向量平行的关系,最多是2个向量在同一条直线上
3 矩阵(matrix)
3.1 矩阵的定义
严格定义:矩阵,数学术语。在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合 ,最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。
- 矩阵是一个二维数组,其中的每一个元素由两个索引来决定 A(i,j)
- 很多编程语言里把每1行看成1个对象,每1列看成属性/特征
- 可以说,矩阵就是2维数组
- 矩阵A(i,j) 比如 ( a11,a12 ; a21,a22 )
3.2 矩阵和向量的关系
观点1
- 基础观点
- 矩阵是由多个向量构成的,一般认为是多个列向量(基)构成的
- 矩阵就是一个在N维度空间里的坐标,这个坐标包含多个向量
观点2
- 计算时,可以认为向量就是一种特殊的矩阵
- 列向量就是列矩阵
- 行向量就是行矩阵
3.3 方阵
- 矩阵里,行数=列数的矩阵叫做方阵
- 方阵有很多很好的特殊属性
4 张量(tensor):向量,矩阵都可以看成张量
4.1 张量的定义
- 可以说,张量就是2维数组
- 矩阵A(i,j,k) 比如 ( a11,a12 ; a21,a22 ; a31,a32 )
- 张量的定义
- 一个数字的标量,称为0阶张量
- 一个数组的这种向量,(1,2),称为1阶张量 (相当于1个维度)
- 2个数组的这种矩阵,比如(1,2;1,1),称为2阶张量 (相当于2个维度)
- 超过二维的数组,如一个三维的A(i,j,k),就称为3阶张量
4.2 更多维度的张量,举例子
- 3维=时间序列
- 4维=图像
- 5维=视频
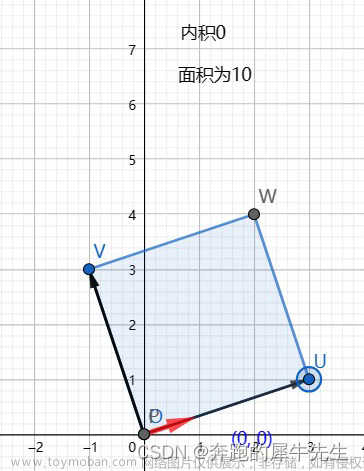
4.3 张量的图形表示
下面用的是网上的2张图,不是我自己的


5 具体例子说明 向量,矩阵,张量
先把维度的概念界定清晰文章来源:https://www.toymoban.com/news/detail-762609.html
- 头脑里要明白,空间的维度是一种3D世界的空间维度概念
- 头脑里要明白,向量/矩阵/张量的维度是一种向量空间/张成空间的维度概念
- 在向量空间/张成空间里,每个向量都 = 一个基于原点和基的一个射线线段/一个点/一个终点的坐标值数组。
5.1 向量
- 向量就是一组数
- 单位向量本身维度是指,向量里标量的个数,这个维度可以很大。
- 但是在空间上就是一根线,在空间上是一维的
- 也就是说空间上1维的向量,可能是N维向量
- 1维向量
- (0)
- [3]
- 2维向量
- (0,1)
- [4,5]
- 3维向量
- (0,1,2)
- [3,4,5]
- N维(有限维度,可以很大很大)
- (1,2,3...... 1001)
5.2 矩阵
- 矩阵是数组的数组,矩阵是一种数组的嵌套,但是只能嵌套2层数组/向量
- 矩阵=[数组] =[[] , [] ,....]
- 矩阵内部的行列数n*m, 一般来说矩阵的维度dim=矩阵的秩<=n/m
- 但是矩阵在空间上看是二维的
- (0,1,2; 3,4,5)
- [ [1,2,3...... 1001] , [1,2] ]
5.3 张量
- 张量在空间上看是3维,4维,或者更大
- 从空间上,很难用图形描述了
- 3阶标量 [ [1,0,0] [0,1,0] [0,0,1] ]
- 4阶标量 [ [1,0,0] [0,1,0] [0,0,1] [0,0,1] ]
- ...
5.4 常见的写法区别
- 注意写法:
- 数量→逗号 一个维度的数量
- 维度→分号; 分隔不同的维度
5.5 一个比较灵活的实际例子
- 下表仍然是一个表现上是1个2维表,其实也可以看成N维的张量?
- 可以灵活设计,做成2维的,或者3维度的都可以,因为可以选择把一部分属性,合并成同一个维度
| 价格 | 数量 | 颜色 | 重量 | 尺寸 | |
| A | 10 | 5 | red | 10 | 5 |
| B | 50 | 2 | blue | 3 | 2 |
| C | 100 | 1 | yellow | 1 | 1 |
| D | 30 | 10 | green | 5 | 3 |
5.5.1 上面这个表直接看成一个5阶张量是没问题的
- 上面这个表直接看成一个5阶张量是没问题的
- 空间上不好表现
- 比如可以花成5条坐标轴,但肯定不是正交那种样式了
5.5.2 强行合并一些列,把总列数表为3列
- 留下ID,时间,属性这3列,可以画成一个 3D坐标系
- 看的视角:ID,时间,属性(包括很多子属性,每个子属性1列)
- 也可以这么看:x为ID,y为property 意味着,ID-价格,ID-数量,ID-颜色,,,,可以组成N张二维表,这些二维表可以叠在一起。形成了Z轴
 文章来源地址https://www.toymoban.com/news/detail-762609.html
文章来源地址https://www.toymoban.com/news/detail-762609.html
到了这里,关于线性代数的学习和整理3:标量,向量和张量的定义和对比的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!