一、粒子群算法的实现思路
粒子群算法(Particle Swarm Optimization,PSO)是于1995年被Kennedy等人提出的一种模拟自然界中鸟群进行觅食过程的一种群智能优化算法,该算法将待求解问题的每一个候选解视作鸟群中的每一个个体的具体位置信息,每个候选解对应的最优适应度值作为每个个体在该位置处所能搜索到的食物的量,通过个体间位置信息的相互交流来发现目标范围内的最优适应度值对应的最优候选解。
在使用粒子群算法进行优化问题的求解时,需要进行理解的概念主要有两个,一个是粒子的位置信息,一个是粒子的速度信息。
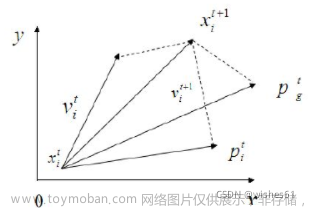
粒子的位置信息通常对应着待优化问题的候选解,最初需要对此位置信息在目标范围内进行初始化,然后通过此位置信息计算获得此粒子的适应度值,在每次迭代的过程中粒子需要对自己的位置信息进行更新,具体的更新公式如下:
该公式表示个体i在第t次迭代后的位置信息等于在第t次迭代前的位置信息加上第t次迭代时的速度。
在对个体的位置信息进行更新前,需要通过计算获得个体新的速度信息,这一速度信息一般包括了个体在接下来的一次迭代过程中的移动方向和移动距离,其具体的计算公式如下:
等号右边分成三部分,第一部分是惯性因子乘以上一次迭代时的速度,第二部分为自我学习部分,括号中是该个体历史最优位置信息减去该个体上一次迭代时的位置信息,第三部分为种群学习部分,括号中是该种群历史最优位置信息减去该个体上一次迭代时的位置信息。w为惯性因子,c1、c2为加速因子,其中前者为每个粒子的个体学习加速因子,后者为每个粒子的全局学习加速因子,通常这两个数被设置为常数2,但也可设为其他的常数,但其取值范围处于[0,4]之间,r1与r2均为0到1之间的随机数。
二、算法步骤
粒子群算法的算法步骤可以总结如下:
- 按照问题的候选解形式,在目标范围内随机生成多个种群个体,然后分别计算出每个个体的适应度值;
- 将每个个体适应度值作为其历史最优适应度值,对应的位置信息作为历史最优的位置信息;
- 比较种群中所有个体的适应度值,将最好的适应度值作为全局历史最优适应度值,将对应的位置信息作为全局历史最优位置信息;
- 对每个个体依次其速度信息和位置信息进行更新;
- 对更新后的个体计算它们的适应度值,将此适应度值与个体历史最优适应度值进行比较,若更新后的适应度值更优,则对个体历史最优适应度值以及对应的个体历史最优位置信息进行更新,反之则不更新;
- 选出此时种群中适应度值最优的个体,将其适应度值与全局历史最优适应度值进行比较,若最优的适应度值较全局历史最优适应度值更好,则对全局历史最优适应度值以及对应的全局历史最优位置信息进行更新,反之则不更新;
- 重复步骤4到步骤6,当达到最大迭代次数或满足停止迭代条件后停止迭代,然后输出此时种群中的全局历史最优个体的位置信息。
三、实例
待求解问题:
Rosenbrock’s,取值范围为[-10,10],取值范围内的理想最优解为0,将其搜索的空间维度设为20。
实现源码:
#库的导入
import numpy as np
import random
import matplotlib.pyplot as plt
#待求解问题
def function(x):
y1 = 0
for i in range(len(x) - 1):
y2 = 100 * ((x[i + 1] - x[i] ** 2) ** 2) + (x[i] - 1) ** 2
y1 = y1 + y2
y = abs(0 - y1)
return y
rangepop=[-10,10] #取值范围
pn=30 #种群数量
iterators = 1000 #迭代次数
w=0.9 #惯性因子
#两个加速系数
c1=2
c2=2
#a1用于存储种群个体位置信息,v用于存储种群个体移动速度,fitness用于存储个体适应度值
a1=np.zeros((pn,20))
v = np.zeros((pn, 20))
fitness=np.zeros(pn)
#对种群个体、移动速度进行初始化,计算初始适应度值
for j in range(pn):
a1[j] = np.random.uniform(low=-10, high=10,size=(1, 20))
v[j] = np.zeros((1,20))
fitness[j] = function(a1[j])
#allpg,bestpg分别表示种群历史最优个体和适应度值
allpg,bestpg=a1[fitness.argmin()].copy(),fitness.min()
#poppn,bestpn分别存储个体历史最优位置和适应度值
poppn,bestpn=a1.copy(),fitness.copy()
#bestfitness用于存储每次迭代时的种群历史最优适应度值
bestfitness=np.zeros(iterators)
#开始迭代
for i in range(iterators):
print("generation:",i)
for m in range(pn):
r1 = np.random.rand()
r2 = np.random.rand()
#计算移动速度
v[m]=w*v[m]+c1*r1*(poppn[m]-a1[m])+c2*r2*(allpg-a1[m])
#计算新的位置
a1[m]=a1[m]+v[m]
#确保更新后的位置在取值范围内
a1[a1<rangepop[0]]=rangepop[0]
a1[a1>rangepop[1]]=rangepop[1]
#计算适应度值
fitness[m] = function(a1[m])
#更新个体历史最优适应度值
if fitness[m]<bestpn[m]:
bestpn[m]=fitness[m]
poppn[m]=a1[m].copy()
#更新种群历史最优适应度值
if bestpn.min()<bestpg:
bestpg=bestpn.min()
allpg=poppn[bestpn.argmin()].copy()
bestfitness[i]=bestpg
print("the best fitness is:",bestfitness[i])
#将结果进行绘图
fig=plt.figure(figsize=(12, 10), dpi=300)
plt.title('The change of best fitness',fontdict={'weight':'normal','size': 30})
x=range(1,1001,1)
plt.plot(x,bestfitness,color="red",label="PSO",linewidth=3.0, linestyle="-")
plt.tick_params(labelsize=25)
plt.xlabel("Epoch",fontdict={'weight':'normal','size': 30})
plt.ylabel("Fitness value",fontdict={'weight':'normal','size': 30})
plt.xticks(range(0,1001,100))
plt.legend(loc="upper right",prop={'size':20})
plt.savefig("PSO.png")
plt.show()
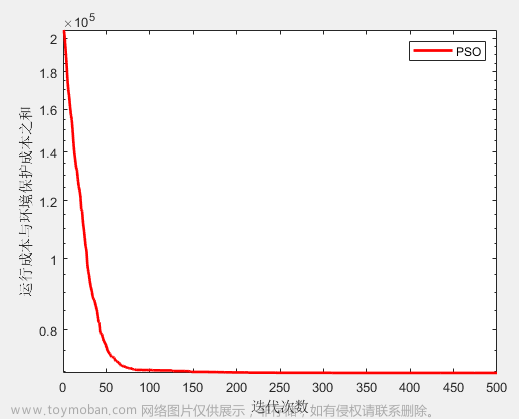
图中横轴为迭代次数,纵轴为最优适应度值。 文章来源:https://www.toymoban.com/news/detail-762647.html
文章来源:https://www.toymoban.com/news/detail-762647.html
参考源码文章来源地址https://www.toymoban.com/news/detail-762647.html
到了这里,关于智能优化算法之粒子群算法(PSO)的实现(Python附源码)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!