上文总结:
① ABtest主要是对比两组数据,判断变量的影响。
② 但我们知道,数据之间的差异,既有可能是随机误差,也可能是变量导致的本质差异。
③ 所以,我们需要根据随机误差的概率,判断数据差异究竟是随机误差,还是由变量影响导致的本质差异。
- 如果随机误差概率大,则无法证明变量是否有影响
- 如果随机误差概率极小,则可认为数据差异是变量影响导致的本质差异。
————————————————
原文链接:https://blog.csdn.net/weixin_50348308/article/details/129732894
根据随机误差的概率大小,判断两个数据差异是随机误差,还是本质差异的方式,是统计学中的显著性检验本质。
那么显著性检验,是如何计算随机误差的概率?又如何判断概率大小的呢?
二、显著性检验原理
假设检验中的显著性检验,是根据一组数据的分布规律,来计算数据差异的随机性概率大小(即随机误差的概率),进而根据概率判断数据差异究竟是随机差异,还是变量导致的本质差异。
因此,我们需要先了解数据的分布规律。
1. 数据分布规律
在生活中,大量数据通常呈现出对应的分布规律,我们之前学过的正态分布,则是非常普遍的数值分布规律。
如果数据服从正态分布,那么我们是可以通过数学公式很快计算出数据差异的概率值,进而可以根据概率来判断数据差异的情况。
因此,我们主要讲解的是数据服从正态分布时的显著性检验。
首先,我们来简单回顾一下正态分布。
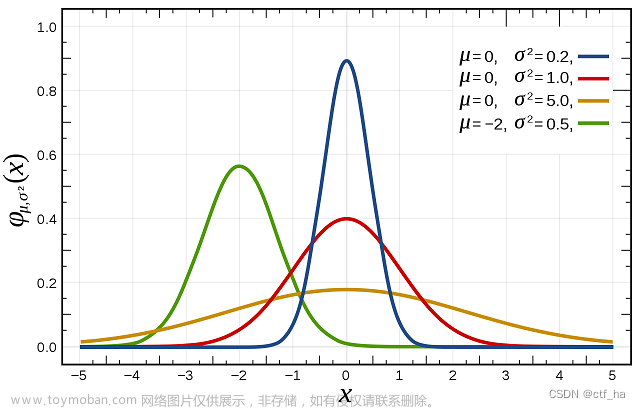
1.1 回顾正态分布
如果一个数据集服从正态分布N(μ,σ),那么这个数据集里的数据分布图像就如下图所示:
均值μ表示曲线的中间位置,标准差σ表示曲线的离散程度。
它对应的概率分布规律就是,数据大概率会落在均值μ的附近,越偏离均值μ,概率越小。
在正态分布中,只要计算除了均值的差异程度,就可以相应地计算出对应的概率。
接下来,我们先看看正态分布中的均值偏离程度及其对应的随机误差概率是如何计算的。
2. 计算均值偏离程度
在正态分布中,均值与均值之间的偏差程度,通常用检验统计量表示。
在理解检验统计量的计算前,先了解一下【中心极限定理】
2.1 中心极限定理
- 中心极限定理:当样本量足够大时,样本均值的分布近似服从正态分布
- Excel 实例验证中心极限定理如下图(近似服从正态分布,如果样本量更大,则更接近正态)

中心极限定理,是显著性检验的基础理论。
2.2 认识检验统计量
继续-检验统计量
检验统计量是根据两个数据的均值之差,除以标准误得到的。
它表示两个数据的均值相差几个标准误。(图为z检验时的检验统计量)
总体标准差:σ(抽单个数值作为样本,抽样次数为n)
样本标准差:所有样本偏离样本均值的程度S=
(
Σ
(
x
−
x
−
)
2
)
\sqrt{(Σ(x-x^-)²)}
(Σ(x−x−)2)
(抽单个数值作为样本,抽样次数为n)
- 对所有样本组合得到的均值,会等于总体均值。此时:
样本均值的标准误差:标准差的标准差
(
Σ
(
S
−
S
−
)
2
)
\sqrt{(Σ(S-S^-)²)}
(Σ(S−S−)2),S为每一个样本标准差,总和即为所有样本标准差的标准差
(抽几个数值的样本均值为样本,抽样次数为所有可能的样本组合)
- 但实际我们无法抽取多次样本,来计算样本均值的标准误差,因此一般采用抽取一次样本进行估算,估算公式如下:
标准误= 标准 差 2 / n \sqrt{标准差²/n} 标准差2/n= 方差 / n \sqrt{方差/n} 方差/n= σ 2 / n \sqrt{σ²/n} σ2/n
标准误:当n越大,则表示样本均值与总体均值的误差越小;
当n接近于总体的数量N时(N为无限总体),则z值为0,表示样本均值是总体均值的无偏估计。
当N不是无限总体时,Z值一般有不一样的计算公式:
当样本量n相对较小时,则样本均值与总体均值的偏差也会更大。
用中心极限定理理解更直接,抽样次数增加,样本均值服从均值为总体均值,方差为(总体方差/样本容量)的正态分布。
- 为什么有些资料写着:Z检验,一般要求样本量n>30(或样本量足够大);
- 因为只有当样本量足够大时,样本均值才能近似服从正态分布,进而可以正确计算出检验统计量。

*因此,当样本容量足够大的时候,样本是可以不需要服从正态分布的!!!????
但是,也有个困惑:多次抽样后的样本均值数据,是否能够代表两组原数据进行检验呢?
——【有待验证,但私以为是不行的】
因为虽然样本均值服从正态分布,但若总体不服从正态分布,那么样本均值的检验,是否能够代表总体的检验呢???这个尚未有明确定论。
- 回到检验统计量z值
👉如果检验统计量越大,说明均值偏离越远;
👉如果检验统计量越小,说明均值偏离越近。
- 为什么两组数据的差异,不直接用x-μ就好,非得用检验统计量呢?
理由1:即使是x-μ的值相同,在不同正态分布下,根据x-μ计算出的对应概率是不同的。
(不同的正态分布,有不同的概率密度函数,分门别类去计算太麻烦,可统一转为标准正态分布后计算)
理由2:计算概率值,是通过标准正态分布的概率密度函数计算得到的。
(Excel工具基本是基于标准正态分布的概率密度函数进行计算的)

因此,可以通过将普通正态分布,转化为标准正态分布:N(μ1,σ²)→N(0,1)
转化公式为:z=
x
−
μ
σ
\frac{x-μ}{σ}
σx−μ,它表示,均值相差几个标准差。
(这就像“一头牛值几头猪”一样,用σ作为单位)
- 这样就可以用标准正态分布的概率密度函数来计算概率了。
这时,大大的困惑困住了我!!!!!!!
为什么Z检验统计量公式,跟转化为标准正态分布的公式,不一样呢?
检验统计量:z=
x
−
μ
σ
2
n
\frac{x-μ}{\sqrt{\frac{σ²}{n}}}
nσ2x−μ
转为标准正态公式:z=
x
−
μ
σ
\frac{x-μ}{σ}
σx−μ
我觉得,我......不理解......但就算不管要不要转化为标准正态分布这档子事,光凭检验统计量的公式,也是可以继续应用显著性检验的............唉...
检验统计量:z=
x
−
μ
σ
2
n
\frac{x-μ}{\sqrt{\frac{σ²}{n}}}
nσ2x−μ
计算出检验统计量后,我们就可以计算出对应的随机误差概率值。
3. 计算随机误差概率
著名的【正态分布经验法则-3σ】里的概率,就是通过计算出来的:
-大约68%的观察值将分布在均值 ±1 倍标准差之间,即其 z值在 -1~1 之间;
-大约95%的观察值将分布在均值 ±2 倍标准差之间,即其 z值在 -2~2 之间;
-几乎全部(99.7%)的观察值将分布在均值 ±3 倍标准差之间,即其 z值在 -3~3 之间。

(ps:切比雪夫定理,跟正态分布经验法则。。。并不是一回事)
- 继续随机误差概率
随机误差概率:两组数据的差异,随机性发生的概率。
3.1 回顾随机误差概率
(算了,把我做的课内容放上来吧…)

小猫咪太可爱了,屋里女猪脚
回顾总结:要计算服从正态分布下的随机误差概率。
3.2 左、右尾 P值
概率密度函数,本身就是一个导函数。它的积分(即面积),就是原函数的值。
左尾 P值,是正常概率密度函数下的积分值。
右尾 P值 = 1-左尾P值
很多人容易混淆,双尾P值的计算,这里要做澄清:
👉 z值<0时,表示在正态中心左侧:
- 计算出的左尾 P值为-∞到z的积分值;
- 计算出的右尾 P值为z到+∞的积分。
👉 z值>0时,表示在正态中心右侧:
- 计算出的左尾 P值为-∞到z的积分值;
- 计算出的右尾 P值为z到+∞的积分。
左右为并不会因为z的正负,而有不同的计算公式!!!!
👉 z值<0时,表示在正态中心左侧:
我们可以通过数学相关的工具,直接求出检验统计量所对应的随机误差概率值,简称P值。
例如下图,是我用Excel计算出的P值,你暂时只需要简单了解。
(插工具图)
计算出检验统计量对应的随机误差概率P值后,接下来,我们将根据P值进行判断数据差异的情况。
判断随机误差概率
我们知道,当随机误差概率P值较大时,无法判断出两组数据的差异,究竟是随机出现的差异,还是变量影响导致的本质差异。
在显著性检验中,这种情况通常认为是数据差异不显著,两组数据本质无差异。
只有当随机误差概率P值极小时,我们才能认为两组数据的差异,不太可能是随机出现的,应该是变量影响导致的本质差异。
在显著性检验中,这种情况通常认为是数据差异显著,两组数据本质有差异。
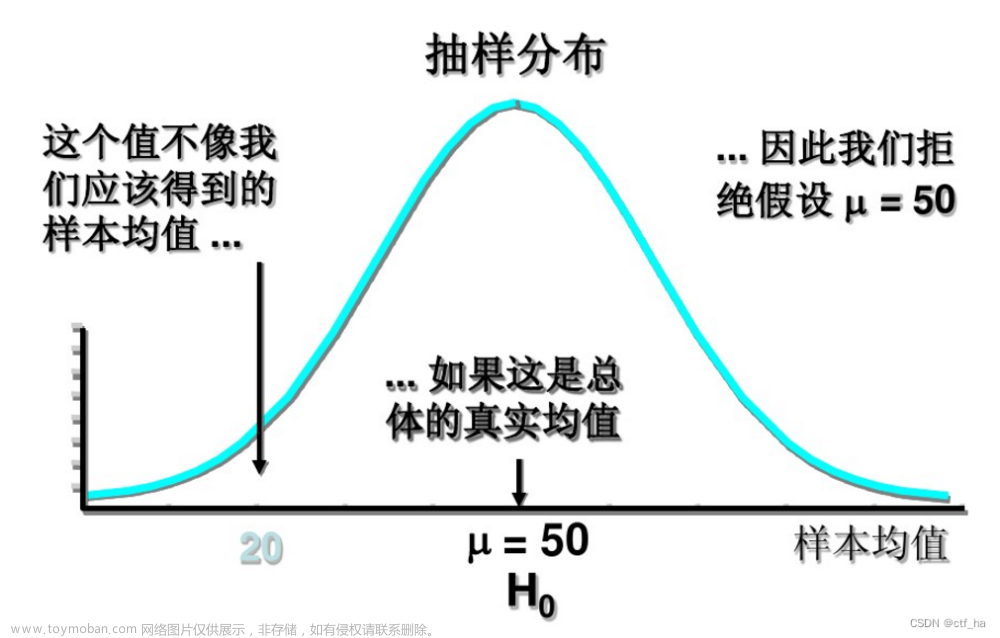
那么随机误差概率P值,要多小,才能认为是两组数据的差异不可能是随机误差,而是变量影响导致的本质差异呢?
这就需要我们人为去规定一个概率P值的界限,而这个界限通常称为显著性水平α。
在统计学应用中,通常将这个显著性水平α设置为0.05,它表示样本均值落在距离总体均值大约正负1.96个标准差位置之外的两侧区域时,即检验统计量为正负1.96时,计算出的随机误差概率值0.05。
正态分布曲线下的面积,即为概率值。
显著性水平α所对应的界限范围内的中间区域,一般称为置信区间。
显著性水平α所对应的界限范围外的两侧区域,一般称为拒绝域。
(插图)
如果计算出的P值小于显著性水平α(即P值<0.05),说明P值对应的检验统计量落在拒绝域内,统计学上通常称为 差异显著。
这时,随机误差概率P值偏小,我们可以认为两组数据的差异几乎不太可能是随机出现的,应该是变量导致的本质差异。
因此,P值<α,表示差异显著,我们认为这两组数据是本质差异。
就比如,我们在池塘A里几乎不可能捞出鳄鱼,但在池塘B却一次捞上鳄鱼,因此我们认为池塘A和池塘B本质是不同的,有可能池塘A是普通水池,池塘B是专业养殖鳄鱼池。
如果计算出的P值大于显著性水平α(即P值>0.05),P值对应的检验统计量落在置信区间里,统计学上通常称为 差异不显著。
这时,随机误差概率P值较大,说明这两组数据的差异,既有可能是随机出现的,也有可能是变量导致的本质差异。
因此,P值>α,表示差异不显著,我们无法判断这两组数据本质上是否有差异。
就比如,在池塘A里,有较大可能捞到鳄鱼,在池塘B一次捞上鳄鱼,并无法说明池塘A和池塘B本质是否相同。有可能池塘A是野生水池,池塘B是专业养殖鳄鱼池;也有可能池塘A、B都是专业养殖鳄鱼池。
以上就是数据服从正态分布时,对两个数据差异进行显著性检验的统计学原理。
显著性检验原理总结
总结来看,就是当数据服从正态分布时,先计算出两组数据均值的偏差程度(即检验统计量),再计算出对应的随机误差概率(即随机误差概率P值),最后判断随机误差概率(规定显著性水平α),明确数据差异的显著性。
(插图)
如果P值>α,说明数据差异不显著,无法判断差异是随机误差,还是本质差异。
如果P值<α,说明数据差异显著,认为是变量影响导致的本质差异。
刚才介绍的基于正态分布的假设检验,是一个总体数据服从正态分布情况下,对样本均值与总体均值差异的检验,属于单样本检验。这种统计情况一般使用单样本Z检验。
例如检验一小批人的薪资均值(样本均值)与全国薪资均值(总体均值)的差异情况。
除了单样本Z检验外,还有其他的显著性检验方式。文章来源:https://www.toymoban.com/news/detail-762695.html
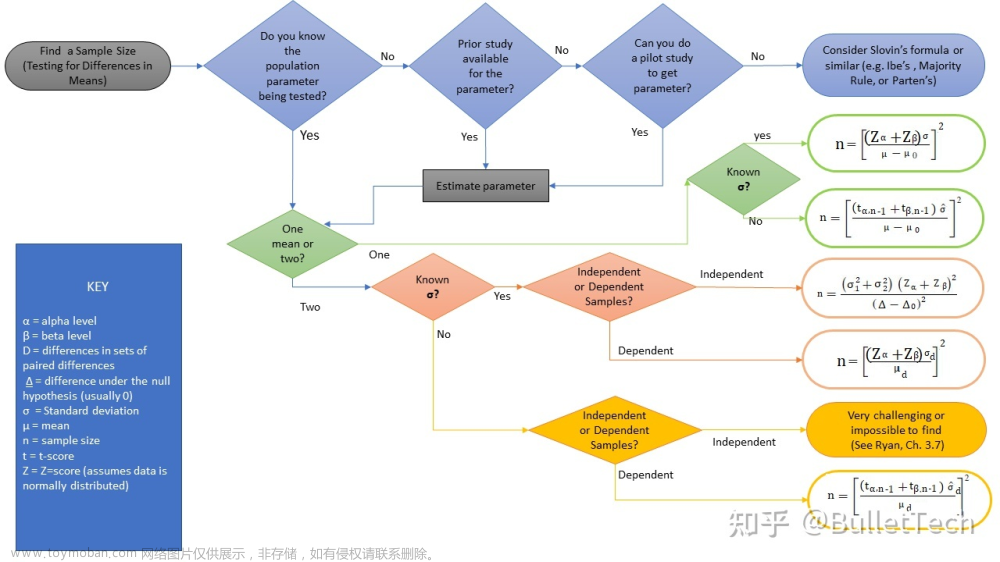
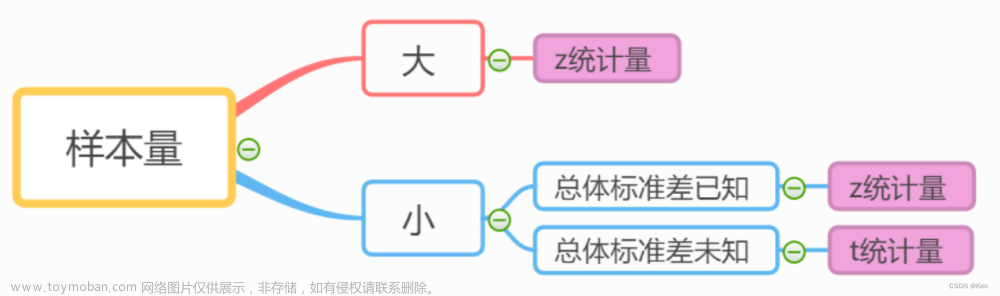
显著性检验方式及区别
实际进行均值差异的显著性检验时,会有多种检验方式。下图是我们常用的4种检验统计方式:单样本z检验、双独立样本z检验、单样本t检验、双独立样本t检验。
不同检验方式的差别在于,根据数据统计情况的不同,导致检验统计量的计算公式不同。
(插图)
例如,在实际收集数据时,总体数据量太大,我们很难采集到总体数据。那么这种情况下,我们可以用服从正态分布的样本来代替总体。用一个样本代替一个总体的单样本检验,一般使用单样本T检验方式。
如果采集的数据是两个服从正态分布的样本数据,且这两个样本数据之间是相互独立的。那么就可以选择双样本独立T检验。
具体选择哪个检验方式,还是要因地制宜,根据根据不同的数据统计类型、不同的数据关系、不同的分布形态来选择。文章来源地址https://www.toymoban.com/news/detail-762695.html
到了这里,关于检验统计量的深度认识(乱七八糟的草稿)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!