lintcode 1840 · 矩阵还原【中等 vip 二维前缀和数组】-Toy模板网

这篇具有很好参考价值的文章主要介绍了lintcode 1840 · 矩阵还原【中等 vip 二维前缀和数组】。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

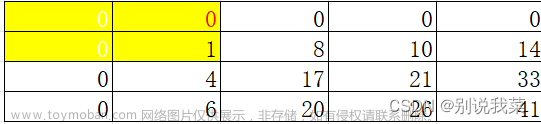
题目

https://www.lintcode.com/problem/1840文章来源地址https://www.toymoban.com/news/detail-762728.html

现有一个n行m列的矩阵
before，对于before里的每一个元素
before[i][j]，我们会使用以下算法将其转化为
after[i][j]。现给定after矩阵，请还原出原有的矩阵before。

s = 0
for i1: 0 -> i
    for j1: 0 -> j
        s = s + before[i1][j1]
after[i][j] = s


1≤n,m≤1000

样例
样例1：

输入:
2
2
[[1,3],[4,10]]
输出: 
[[1,2],[3,4]]
解释:
before:
1 2
3 4

after:
1 3
4 10

前置知识

前缀和数组
二维数组前缀和数组

参考答案

public class Solution {
    /**
     * @param n: the row of the matrix
     * @param m: the column of the matrix
     * @param after: the matrix
     * @return: restore the matrix
     */
    public int[][] matrixRestoration(int n, int m, int[][] after) {
        /*
      after定义其实就是二维数组的前缀和
      after[i][j]=after[i-1][j]+after[i][j-1]+before[i][j]-after[i-1][j-1]
      可以推导处于before[i][j]的公式
      before[i][j]= after[i][j]-after[i-1][j]-after[i][j-1]+after[i-1][j-1]
       */
        int[][] before = new int[n][m];
        for (int i = 0; i <n ; i++) {
            for (int j = 0; j <m ; j++) {
               int cur = after[i][j];
                if(i> 0){
                    cur-= after[i-1][j];
                }
                if(j> 0){
                    cur -= after[i][j-1];
                }

                if(i>0 && j>0){
                    cur += after[i-1][j-1];
                }

                before[i][j] = cur;
            }
        }

        return before;
    }
}