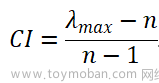AHP层次分析法
1.层次分析法
实现标准之间相对重要程度,并给出决策方案中每个标准的权重,利用权数求出各个方案的优劣次序。
2.应用步骤
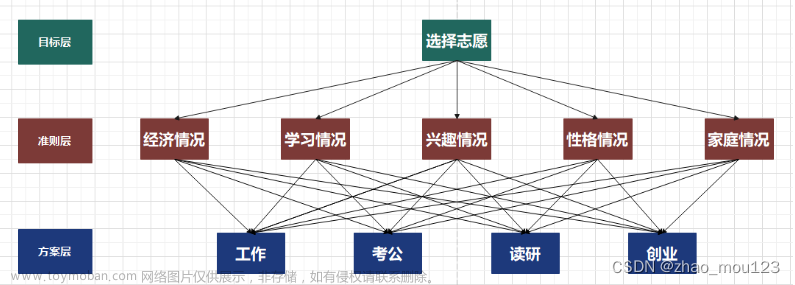
1.建立层次结构模型
该层主要有三个方面:
- 目标层
- 准则层
- 领域层(各种解决问题的措施和方案)
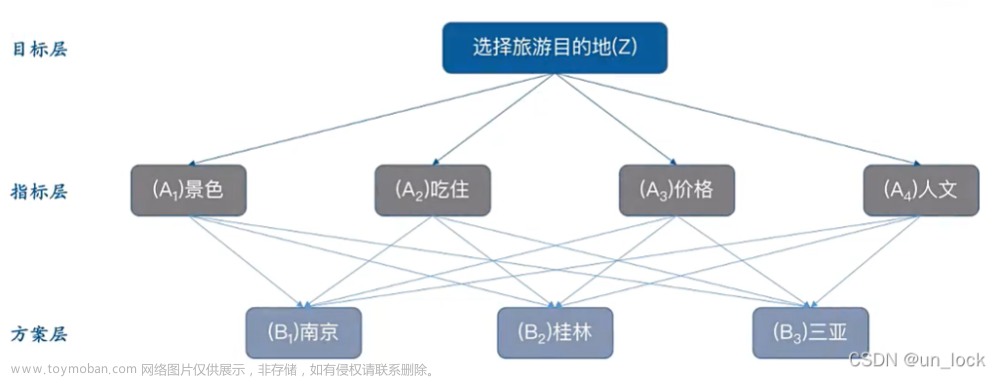
这里选择了一个旅游问题的层次分析模型来直观的展示三个层的关系:
如果将三个层放在实际解决问题的时候,其依次对应的就是:
目标层:考虑解决什么样的问题?
准则层:考虑解决问题的决策因素?
领域层:考虑解决问题的方案。
2.构造判断矩阵
1)判断矩阵标度方法表
比较各层各个因素对于下一层的重要性,其判断矩阵需要使用判断矩阵aij的标度方法表:
2) 构造判断矩阵A:
先构造方案层的各个判断矩阵(Pn——Cn):
构造准则层对于目标层的各个判断矩阵(Cn——O):

3.计算单层权向量并做一致性检验
能否确认层次单排序,需要进行一致性检验,一致性检验指的是判断矩阵确定不一致的允许范围。
4.一致性检验
1) 层次分析法中构造的判断矩阵是正互反矩阵。
小tips:正互反矩阵中各行各列是否呈倍数关系,即可判断其是否为一致矩阵。
2)一致性检验原理:
检验我们构造的判断矩阵和一致矩阵是否有太大的差别,也就是检验特征值和n相差大小。
3)一致性检验数学原理

由引理可知:一直矩阵有一个特征值为n,其余特征值均为0。并且,当特征值为n时,对应的特征向量刚好为:

从上图可以看出,当判断矩阵越不一致时,最大特征值与n相差就越大。
4)一致性检验计算过程


Q1:为什么要这样构造CI,为什么要以0.1为划分依据。答:通过多次蒙特卡罗模拟得到的最佳方案。
5.一致矩阵计算权重
1)求权重实例:


2)求权重的几种方法:
方法一:算术平均法求权重
方法二:几何平均法求权重
方法三:特征值法求权重
步骤1:求出矩阵A的最大特征值和对应的特征向量
步骤2:对求出的特征向量进行归一化得到权重
6.层次总排序及其一致性检验
- 计算某一层次所有因素对于最高层(总目标)相对重要性的权重,称为层次总排列。
- 这一过程是从最高层次到最低层次依次进行。
3.层次分析法的一些局限性
1)评价的决策层不能太多,太多的话n会很大,判断矩阵和一致矩阵差异性可能会很大

2) 如果决策层中指标的数据是已知的,如何利用这些数据来使得评价更标准?
4.单层AHP应用(领域层已经给出):旅游目的地选择代码实例
- Cn层到O层的判断矩阵:

- 输入判断矩阵:
import numpy as np
A=np.array([[1,1/2,4,3,3],
[2,1,7,5,5],
[1/4,1/7,1,1/2,1/3],
[1/3,1/5,2,1,1],
[1/3,1/5,3,1,1]])
print(A)

3. 判断矩阵的形状:
[m,n]=A.shape
print(m,n)

4. 输出矩阵A的特征值和特征向量:
V,D=np.linalg.eig(A)
print("特征值为:")
print(V)
print("特征向量:")
print(D)

5. 输出最大特征值和特征向量:
max_V=np.max(V)
print(max_V)
k=[i for i in range(len(V)) if V[i]==max_V]
max_D=-D[:,k]
print(max_D)

6. 计算权重:
weight=np.zeros((n,1))
weight
for i in range(0,n):
weight[i]=max_D[i]/np.sum(max_D)
Q=weight
print(Q)

7. 一致性检验:
CI=(max_V-n)/(n-1)
RI=[0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45,1.49,1.52,1.54,1.56,1.58,1.59]
RI_1=RI[n-1]
CR=CI/RI_1
if CR>=0.1:
print('没有通过特征值检验')
else:
print('通过一致性检验')

8. 计算评分:
假设已知苏杭、北戴河、桂林三个方案层对于准则层的评分:
p = np.mat('8 7 6 8 7;7 8 8 7 8;5 7 6 7 7')
score=p*Q
for i in range(len(score)):
print("score{}:".format(i),float(score[i]))
 文章来源:https://www.toymoban.com/news/detail-763004.html
文章来源:https://www.toymoban.com/news/detail-763004.html
5.多层AHP应用:旅游选择问题代码实例
import numpy as np
def AHP(array_matrix):
#N的维度(行)
N=array_matrix.shape[0]
#RI表
list_RI=[0,0,0.52,0.89,1.12,1.26,1.36,1.41,1.46,1.49,1.52,1.54,1.56,1.58,1.59]
#求特征值和特征向量
arr_V,arr_D=np.linalg.eig(array_matrix)
#求最大特征值
max_arr_V=np.max(arr_V)
#最大特征值对应的index
max_index=[i for i in range(len(arr_V)) if arr_V[i]==np.max(arr_V)]
max_arr_D=-arr_D[:,max_index]
#特征向量归一化(求权重)
max_arr_D=max_arr_D/sum(max_arr_D)
CI=(max_arr_V-N)/(N-1)
RI=list_RI[N-1]
#进行一致性检验
is_consistence=False
if N<3:
is_consistence=True
elif CI<0.1:
is_consistence=True
else:
is_consistence=False
#返回最大特征值,最大特征向量,是否满足一致性检验
return max_arr_V,max_arr_D,is_consistence
a=np.array(["苏杭","北戴河","桂林"])
#Cn——O 准则层——目标层判断矩阵
A=np.array([[1,1/2,4,3,3],[2,1,7,5,5],[1/4,1/7,1,1/2,1/3],[1/3,1/5,2,1,1],[1/3,1/5,3,1,1]])
#Pn——Cn 领域层——准则层判断矩阵
B1 = np.array([[1,2,4],[1/2,1,2],[1/4,1/2,1]])
B2 = np.array([[1,1/3,1/8],[3,1,1/3],[8,3,1]])
B3 = np.array([[1,1,3],[1,1,3],[1/3,1/3,1]])
B4 = np.array([[1,3,4],[1/3,1,1],[1/4,1,1]])
B5 = np.array([[1,1,1/4],[1,1,1/4],[4,4,1]])
#将准则层因素判断矩阵合并方便计算
B=np.array([B1,B2,B3,B4,B5])
#返回准则层——目标层判断矩阵的 最大特征值、对应特征向量、是否满足一致性检验
A_max_arr_V,A_max_arr_D,A_is_consistence=AHP(A)
#分别返回判断矩阵B的 最大特征值、对应特征向量、是否满足一致性检验
B_max_arr_V=[]
B_max_arr_D=[]
All_B_is_consistence=[]
for i in B:
max_B_arr_V1,max_B_arr_D1,B_is_consistence=AHP(i)
B_max_arr_V.append(max_B_arr_V1)
B_max_arr_D.append(max_B_arr_D1)
All_B_is_consistence.append(B_is_consistence)
if not A_is_consistence:
print("准则层对目标层的判断矩阵未通过一致性检验,请进行修改")
else:
if not all(All_B_is_consistence):
for i in range(len(All_B_is_consistence)):
if not All_B_is_consistence[i]:
print("方案曾对于准则层各个因素判断矩阵第"+str(i+1)+"个矩阵未通过一致性检验,请进行修改")
else:
#总排序:准则层的最大特征向量的转置乘以目标层的最大特征向量,找到总排序中最大的
w_total=np.array(B_max_arr_D).T.dot(A_max_arr_D)
print("所有判断矩阵均通过一致性检验!\n方案层对目标层的权重为:")
print(w_total)
choose=np.argmax(w_total)
print(choose)
print("最佳方案为第"+str(np.argmax(w_total)+1)+"个方案,该方案为"+a[np.argmax(w_total)])
输出方案结果:
综上所述,AHP层次分析法求解最终方案为桂林文章来源地址https://www.toymoban.com/news/detail-763004.html
到了这里,关于【AHP层次分析法】原理+应用步骤+旅游目的地选择实例应用的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!