算法与数据结构--二叉搜索树与自平衡二叉搜索树

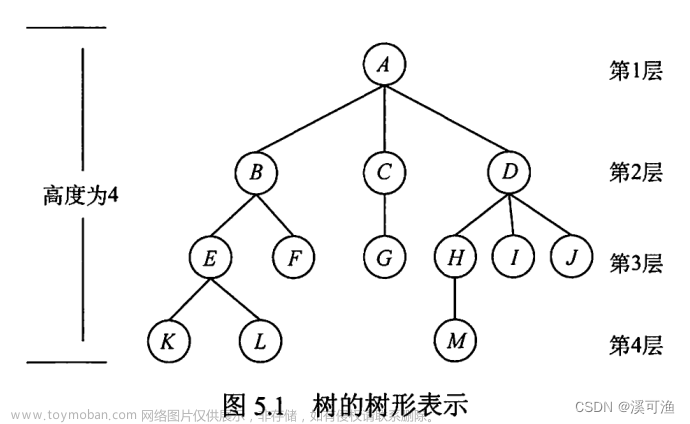
0.字典（即c++的map）

注：字典的 "member运算" 指的是检查字典中是否存在某个特定的键的操作，即查询操作。

如果我们使用数组来实现字典/map，虽然使用二分法查询也可以达到logn，但是的话插入和删除太慢了。使用链表实现的话虽然插入和删除是O(1)，但是查询的话达到了O(n)，也不可取。

因此人们发明了自平衡二叉查找树，在保证查找效率的同时，又保证了插入和删除的效率，从而更好的实现字典。

c++的map和set就是用红黑树来实现的（一种特殊的自平衡二叉搜索树）。而unorder_map使用哈希表实现的。

1.二叉查找树--BST

在讲自平衡二叉搜索树之前，我们要先明白什么是二叉搜索树。

二叉查找树（Binary Search Tree），是具有如下性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

二叉搜索树作为一种经典的数据结构，它既有链表的快速插入与删除操作的特点，又有数组快速查找的优势；所以应用十分广泛，例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。

复杂度：使用二叉搜索树进行添加，删除，搜索的平均时间复杂度都为O(logn)

特点：

2.自平衡二叉查找树--AVL树

1.为什么要有AVL树

二叉查找树虽然平均添加，删除，查找效率为O(logn)，但是却不稳定，比如像上面这张图，在最坏的情况下，也就是该二叉树不平衡的时候，效率又降到了O(n)。

所以我们要想办法让这颗二叉查找树平衡，让结点平均地分布在树的两侧，从而提高算法的稳定性，于是就发明了自平衡二叉搜索树，即AVL树。

2.AVL树的定义

3.如何构建AVL树

具体流程：

元素插入二叉搜索树中->判断结点是否平衡，具体是那种情况的不平衡->根据所处的不平衡情况进行不同的调整策略

当遇到结点不平衡时：

根据插入元素的落点，调整策略分为四种情况，插入元素落入以下4个子树的情况分别对应着四种状态。

【1】右旋--LL型状态

这时候对A结点，也就是根结点使用右旋操作进行调整。A连接左子树的右子树，A称为B的右子树。

【2】左旋--RR型状态

这时候对根结点使用左旋操作。

【3】先左旋后右旋--LR型状态

采用LR双旋。

【4】先右旋后左旋--RL型状态

采用RL双旋。

RL双旋等效于先对C右旋，再对A左旋。

具体代码

gpt生成，以后有时间再自己写一遍文章来源地址https://www.toymoban.com/news/detail-763282.html

#include <iostream>
#include <algorithm>

// AVL节点的定义
struct AVLNode {
    int data;
    AVLNode* left;
    AVLNode* right;
    int height;

    AVLNode(int value) : data(value), left(nullptr), right(nullptr), height(1) {}
};

// 获取节点的高度
int getHeight(AVLNode* node) {
    if (node == nullptr)
        return 0;
    return node->height;
}

// 计算平衡因子
int getBalanceFactor(AVLNode* node) {
    if (node == nullptr)
        return 0;
    return getHeight(node->left) - getHeight(node->right);
}

// 更新节点的高度
void updateHeight(AVLNode* node) {
    if (node != nullptr) {
        node->height = 1 + std::max(getHeight(node->left), getHeight(node->right));
    }
}

// 右旋转
AVLNode* rightRotate(AVLNode* y) {
    AVLNode* x = y->left;
    AVLNode* T2 = x->right;

    x->right = y;
    y->left = T2;

    updateHeight(y);
    updateHeight(x);

    return x;
}

// 左旋转
AVLNode* leftRotate(AVLNode* x) {
    AVLNode* y = x->right;
    AVLNode* T2 = y->left;

    y->left = x;
    x->right = T2;

    updateHeight(x);
    updateHeight(y);

    return y;
}

// 插入节点
AVLNode* insertNode(AVLNode* root, int key) {
    if (root == nullptr) {
        return new AVLNode(key);
    }

    if (key < root->data) {
        root->left = insertNode(root->left, key);
    } else if (key > root->data) {
        root->right = insertNode(root->right, key);
    } else {
        // 重复的键值不允许插入
        return root;
    }

    // 更新节点的高度
    updateHeight(root);

    // 获取平衡因子
    int balance = getBalanceFactor(root);

    // 进行旋转操作以保持平衡
    // 左子树不平衡
    if (balance > 1) {
        if (key < root->left->data) {
            // 左-左情况，进行右旋转
            return rightRotate(root);
        } else {
            // 左-右情况，先左旋转，再右旋转
            root->left = leftRotate(root->left);
            return rightRotate(root);
        }
    }

    // 右子树不平衡
    if (balance < -1) {
        if (key > root->right->data) {
            // 右-右情况，进行左旋转
            return leftRotate(root);
        } else {
            // 右-左情况，先右旋转，再左旋转
            root->right = rightRotate(root->right);
            return leftRotate(root);
        }
    }

    // 树保持平衡，直接返回根节点
    return root;
}

// 中序遍历 AVL 树
void inOrderTraversal(AVLNode* root) {
    if (root != nullptr) {
        inOrderTraversal(root->left);
        std::cout << root->data << " ";
        inOrderTraversal(root->right);
    }
}

int main() {
    AVLNode* root = nullptr;

    // 插入一些节点
    root = insertNode(root, 10);
    root = insertNode(root, 20);
    root = insertNode(root, 30);
    root = insertNode(root, 15);
    root = insertNode(root, 5);

    // 输出中序遍历结果
    std::cout << "In-order traversal of AVL tree: ";
    inOrderTraversal(root);
    std::cout << std::endl;

    return 0;
}

到了这里，关于算法与数据结构--二叉搜索树与自平衡二叉搜索树的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！