【数据结构】并查集的简单实现，合并，查找（C++）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】并查集的简单实现，合并，查找（C++）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

前言

需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find set)。

举例：

学生小分队s1={0,6,7,8}，成都学生小分队s2={1,4,9}，武汉学生小分队s3={2,3,5}就相互认识了，10个人形成了三个小团体。假设右三个群主0,1,2担任队长，负责大家的出行。
【数据结构】并查集的简单实现，合并，查找（C++）,数据结构,c++,java

【数据结构】并查集的简单实现，合并，查找（C++）,数据结构,c++,java

西安小分队中8号同学与成都小分队1号同学奇迹般的走到了一起，两个
小圈子的学生相互介绍，最后成为了一个小圈子：
【数据结构】并查集的简单实现，合并，查找（C++）,数据结构,c++,java

仔细观察数组中内融化，可以得出以下结论：文章来源地址https://www.toymoban.com/news/detail-763617.html

数组的下标对应集合中元素的编号

数组中如果为负数，负号代表根，数字代表该集合中元素个数

数组中如果为非负数，代表该元素双亲在数组中的下标

一、

1.构造函数

UnionFindSet(size_t size)
		:_set(size,-1)//数组中初始化为-1
		//数组的下标对应集合中元素的编号
		//数组的内容如果是非负数代表这个元素的根的下标
		//数组内容为负数，代表这个数字为根，绝对值为这棵树的大小
		{}

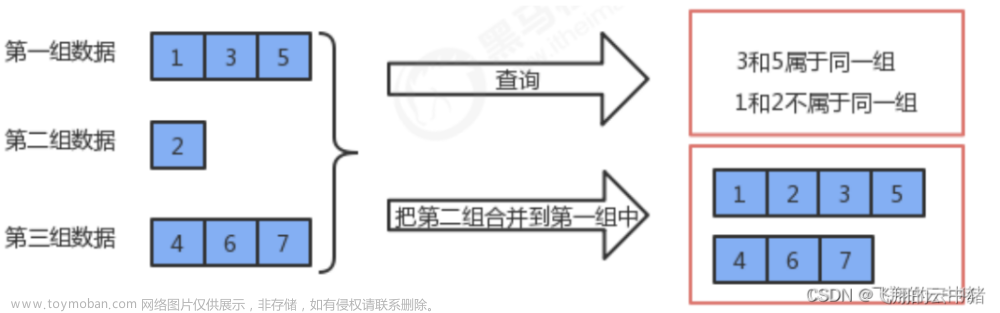
2.查找元素属于哪个集合FindRoot

size_t FindRoot(int x) {//. 查找元素属于哪个集合
			while (_set[x] >= 0) {
				x = _set[x];
			}
			//找到非负的数，这个数的下标即为根的下标
			return x;
		}

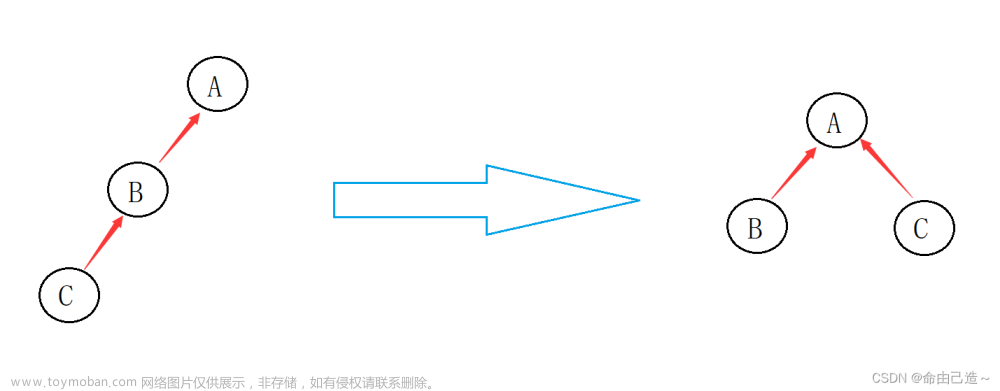
3.将两个集合归并成一个集合Union

void Union(int x1, int x2) {//将两个集合归并同一个集合
			//将元素x2合并进x1
			int root1 = FindRoot(x1);
			int root2 = FindRoot(x2);
			if (root1 != root2) {//保证两个元素不在同一个集合中
				_set[root1] += _set[root2];
				// x2根的内容为负数绝对值为这棵树的数量
				//把x2归并到x1所在集合中
				//x1所在集合的大小发生变化
				_set[root2] = root1;
				//x2的根发生变化
			}
		}

4.查找集合数量SetCount

size_t SetCount() {//统计集合数量（有多少棵树）
			int count = 0;
			for (size_t i = 0; i < _set.size(); i++) {
				if (_set[i] < 0) {
					count++;
				}
			}
			//负数的数量即根的数量即集合的数量
			return count;

		}

5.是否在同一个集合中

bool InSet(int x1, int x2)
	{
		return FindRoot(x1) == FindRoot(x2);
	}

二、源码

class UnionFindSet {
public:
		UnionFindSet(size_t size)
			:_set(size,-1)//数组中初始化为-1
			//数组的下标对应集合中元素的编号
			//数组的内容如果是非负数代表这个元素的根的下标
			//数组内容为负数，代表这个数字为根，绝对值为这棵树的大小
		{}

		size_t FindRoot(int x) {//. 查找元素属于哪个集合
			while (_set[x] >=0) {
				x = _set[x];
			}
			//找到非负的数，这个数的下标即为根的下标
			return x;
		}
bool InSet(int x1, int x2)
{
return FindRoot(x1) ==  FindRoot(x2);
	}
		void Union(int x1, int x2) {//将两个集合归并同一个集合
			//将元素x2合并进x1
			int root1 = FindRoot(x1);
			int root2 = FindRoot(x2);
			if (root1 != root2) {//保证两个元素不在同一个集合中
				_set[root1] += _set[root2];
				// x2根的内容为负数绝对值为这棵树的数量
				//把x2归并到x1所在集合中
				//x1所在集合的大小发生变化
				_set[root2] = root1;
				//x2的根发生变化
			}
		}

		size_t SetCount() {//统计集合数量（有多少棵树）
			int count = 0;
			for (size_t i = 0; i < _set.size(); i++) {
				if (_set[i] < 0) {
					count++;
				}
			}
			//负数的数量即根的数量即集合的数量
			return count;

		}

private:
	vector<int> _set;
 };