class087 动态规划中根据数据量猜解法的技巧【算法】
2023-12-24 14:36:06
算法讲解087【必备】动态规划中根据数据量猜解法的技巧

code1 打 怪 兽
// 贿赂怪兽
// 开始时你的能力是0,你的目标是从0号怪兽开始,通过所有的n只怪兽
// 如果你当前的能力小于i号怪兽的能力,则必须付出b[i]的钱贿赂这个怪兽
// 然后怪兽就会加入你,他的能力a[i]直接累加到你的能力上
// 如果你当前的能力大于等于i号怪兽的能力,你可以选择直接通过,且能力不会下降
// 但你依然可以选择贿赂这个怪兽,然后怪兽的能力直接累加到你的能力上
// 返回通过所有的怪兽,需要花的最小钱数
// 测试链接 : https://www.nowcoder.com/practice/736e12861f9746ab8ae064d4aae2d5a9
// 请同学们务必参考如下代码中关于输入、输出的处理
// 这是输入输出处理效率很高的写法
// 提交以下的code,提交时请把类名改成"Main",可以直接通过
进行如下的思考:
假设a[i]数值的范围很大,但是b[i]数值的范围不大,该怎么做?
假设a[i]数值的范围不大,但是b[i]数值的范围很大,又该怎么做?
比如数据规模是:
1000只坏兽
能力1~104
钱1~10
dp[i][j]:1…i,花的的钱<=j,不能通过-无穷,能通过最大能力值
返回最后一行第一个不是-无穷的j即可
大小dp[1000][1000*10]
i号怪兽的能力a[i],钱b[i]
1)不贿赂i号怪兽: dp[i-1][j],条件:dp[i-1][j]>=a[i]
2)贿赂i号怪兽: dp[i-1][j-b[i]]+a[i],条件:j-b[i]>=0&&dp[i-1][j-b[i]]!=-无穷
比如数据规模是:
能力不大,钱很大
dp[i][j]:1…i号怪兽,通过能力正好是j的最小钱数
如果能通过就是最小的钱,如果不能通过就是+无穷
1)不贿赂i号怪兽: dp[i-1][j],条件:j>=a[i]&& dp[i-1][j]!=+无穷
2)贿赂i号怪兽: dp[i-1][j-a[i]]+b[i],条件:j-a[i]>=0&&dp[i-1][j-a[i]]!=+无穷
初始化dp[0][1…m]=+无穷
返回最后一行最小的值
package class087;
// 贿赂怪兽
// 开始时你的能力是0,你的目标是从0号怪兽开始,通过所有的n只怪兽
// 如果你当前的能力小于i号怪兽的能力,则必须付出b[i]的钱贿赂这个怪兽
// 然后怪兽就会加入你,他的能力a[i]直接累加到你的能力上
// 如果你当前的能力大于等于i号怪兽的能力,你可以选择直接通过,且能力不会下降
// 但你依然可以选择贿赂这个怪兽,然后怪兽的能力直接累加到你的能力上
// 返回通过所有的怪兽,需要花的最小钱数
// 测试链接 : https://www.nowcoder.com/practice/736e12861f9746ab8ae064d4aae2d5a9
// 请同学们务必参考如下代码中关于输入、输出的处理
// 这是输入输出处理效率很高的写法
// 提交以下的code,提交时请把类名改成"Main",可以直接通过
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
public class Code01_BuyMonster {
// 讲解本题的目的不仅仅是为了通过这个题,而是进行如下的思考:
// 假设a[i]数值的范围很大,但是b[i]数值的范围不大,该怎么做?
// 假设a[i]数值的范围不大,但是b[i]数值的范围很大,又该怎么做?
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken() != StreamTokenizer.TT_EOF) {
int n = (int) in.nval;
int[] a = new int[n + 1];
int[] b = new int[n + 1];
for (int i = 1; i <= n; i++) {
in.nextToken();
a[i] = (int) in.nval;
in.nextToken();
b[i] = (int) in.nval;
}
out.println(compute1(n, a, b));
}
out.flush();
out.close();
br.close();
}
// 假设a[i]数值的范围很大,但是b[i]数值的范围不大
// 时间复杂度O(n * 所有怪兽的钱数累加和)
public static int compute1(int n, int[] a, int[] b) {
int m = 0;
for (int money : b) {
m += money;
}
// dp[i][j] : 花的钱不能超过j,通过前i个怪兽,最大能力是多少
// 如果dp[i][j] == Integer.MIN_VALUE
// 表示花的钱不能超过j,无论如何都无法通过前i个怪兽
int[][] dp = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) {
dp[i][j] = Integer.MIN_VALUE;
if (dp[i - 1][j] >= a[i]) {
dp[i][j] = dp[i - 1][j];
}
if (j - b[i] >= 0 && dp[i - 1][j - b[i]] != Integer.MIN_VALUE) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - b[i]] + a[i]);
}
}
}
int ans = -1;
for (int j = 0; j <= m; j++) {
if (dp[n][j] != Integer.MIN_VALUE) {
ans = j;
break;
}
}
return ans;
}
// 就是方法1的空间压缩版本
public static int compute2(int n, int[] a, int[] b) {
int m = 0;
for (int money : b) {
m += money;
}
int[] dp = new int[m + 1];
for (int i = 1, cur; i <= n; i++) {
for (int j = m; j >= 0; j--) {
cur = Integer.MIN_VALUE;
if (dp[j] >= a[i]) {
cur = dp[j];
}
if (j - b[i] >= 0 && dp[j - b[i]] != Integer.MIN_VALUE) {
cur = Math.max(cur, dp[j - b[i]] + a[i]);
}
dp[j] = cur;
}
}
int ans = -1;
for (int j = 0; j <= m; j++) {
if (dp[j] != Integer.MIN_VALUE) {
ans = j;
break;
}
}
return ans;
}
// 假设a[i]数值的范围不大,但是b[i]数值的范围很大
// 时间复杂度O(n * 所有怪兽的能力累加和)
public static int compute3(int n, int[] a, int[] b) {
int m = 0;
for (int ability : a) {
m += ability;
}
// dp[i][j] : 能力正好是j,并且确保能通过前i个怪兽,需要至少花多少钱
// 如果dp[i][j] == Integer.MAX_VALUE
// 表示能力正好是j,无论如何都无法通过前i个怪兽
int[][] dp = new int[n + 1][m + 1];
for (int j = 1; j <= m; j++) {
dp[0][j] = Integer.MAX_VALUE;
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) {
dp[i][j] = Integer.MAX_VALUE;
if (j >= a[i] && dp[i - 1][j] != Integer.MAX_VALUE) {
dp[i][j] = dp[i - 1][j];
}
if (j - a[i] >= 0 && dp[i - 1][j - a[i]] != Integer.MAX_VALUE) {
dp[i][j] = Math.min(dp[i][j], dp[i - 1][j - a[i]] + b[i]);
}
}
}
int ans = Integer.MAX_VALUE;
for (int j = 0; j <= m; j++) {
ans = Math.min(ans, dp[n][j]);
}
return ans == Integer.MAX_VALUE ? -1 : ans;
}
// 就是方法3的空间压缩版本
public static int compute4(int n, int[] a, int[] b) {
int m = 0;
for (int ability : a) {
m += ability;
}
int[] dp = new int[m + 1];
for (int j = 1; j <= m; j++) {
dp[j] = Integer.MAX_VALUE;
}
for (int i = 1, cur; i <= n; i++) {
for (int j = m; j >= 0; j--) {
cur = Integer.MAX_VALUE;
if (j >= a[i] && dp[j] != Integer.MAX_VALUE) {
cur = dp[j];
}
if (j - a[i] >= 0 && dp[j - a[i]] != Integer.MAX_VALUE) {
cur = Math.min(cur, dp[j - a[i]] + b[i]);
}
dp[j] = cur;
}
}
int ans = Integer.MAX_VALUE;
for (int j = 0; j <= m; j++) {
ans = Math.min(ans, dp[j]);
}
return ans == Integer.MAX_VALUE ? -1 : ans;
}
}
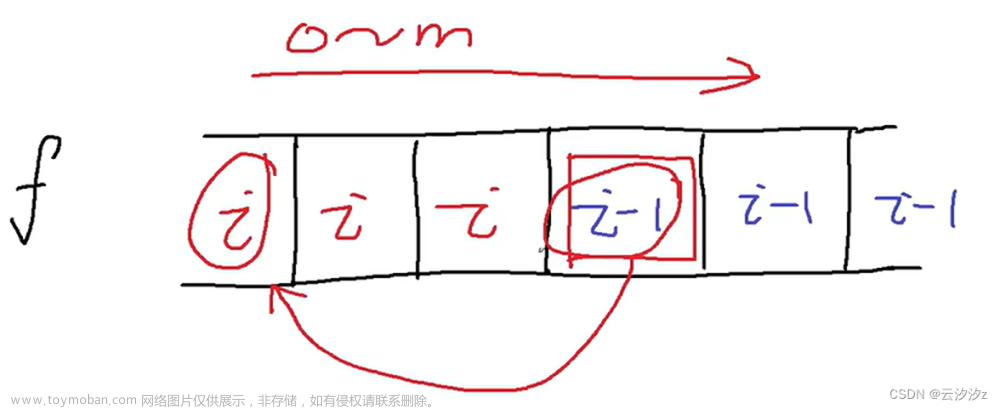
code2 选择k个数字使得两集合累加和相差不超过1
// 选择k个数字使得两集合累加和相差不超过1
// 给定一个正数n,表示1~n这些数字都可以选择
// 给定一个正数k,表示要从1~n中选择k个数字组成集合A,剩下数字组成集合B
// 希望做到集合A和集合B的累加和相差不超过1
// 如果能做到,返回集合A选择了哪些数字,任何一种方案都可以
// 如果不能做到,返回长度为0的数组
// 2 <= n <= 10^6
// 1 <= k <= n
// 来自真实大厂笔试,没有测试链接,用对数器验证
1~n的和:sum
A:sum/2,sum/2+1(sum是奇数)
01背包
//1…i个数,还剩k个,还剩sum累加和
f(i,k,sum)
巧解
前k个数 中间的数 后k个数
构成sum
package class087;
// 选择k个数字使得两集合累加和相差不超过1
// 给定一个正数n,表示1~n这些数字都可以选择
// 给定一个正数k,表示要从1~n中选择k个数字组成集合A,剩下数字组成集合B
// 希望做到集合A和集合B的累加和相差不超过1
// 如果能做到,返回集合A选择了哪些数字,任何一种方案都可以
// 如果不能做到,返回长度为0的数组
// 2 <= n <= 10^6
// 1 <= k <= n
// 来自真实大厂笔试,没有测试链接,用对数器验证
public class Code02_PickNumbersClosedSum {
// 正式方法
// 最优解
public static int[] pick(int n, int k) {
long sum = (n + 1) * n / 2;
int[] ans = generate(sum / 2, n, k);
if (ans.length == 0 && (sum & 1) == 1) {
ans = generate(sum / 2 + 1, n, k);
}
return ans;
}
// 1 ~ n这些数字挑选k个
// 能不能凑够累加和sum
// 能的话,返回挑选了哪些数字
// 不能的话,返回长度为0的数组
public static int[] generate(long sum, int n, int k) {
long minKSum = (k + 1) * k / 2;
int range = n - k;
if (sum < minKSum || sum > minKSum + (long) range * k) {
return new int[0];
}
// 100 15 -> 85
long need = sum - minKSum;
int rightSize = (int) (need / range);
int midIndex = (k - rightSize) + (int) (need % range);
int leftSize = k - rightSize - (need % range == 0 ? 0 : 1);
int[] ans = new int[k];
for (int i = 0; i < leftSize; i++) {
ans[i] = i + 1;
}
if (need % range != 0) {
ans[leftSize] = midIndex;
}
for (int i = k - 1, j = 0; j < rightSize; i--, j++) {
ans[i] = n - j;
}
return ans;
}
// 为了验证
// 检验得到的结果是否正确
public static boolean pass(int n, int k, int[] ans) {
if (ans.length == 0) {
if (canSplit(n, k)) {
return false;
} else {
return true;
}
} else {
if (ans.length != k) {
return false;
}
int sum = (n + 1) * n / 2;
int pickSum = 0;
for (int num : ans) {
pickSum += num;
}
return Math.abs(pickSum - (sum - pickSum)) <= 1;
}
}
// 记忆化搜索
// 不是最优解,只是为了验证
// 返回能不能做到
public static boolean canSplit(int n, int k) {
int sum = (n + 1) * n / 2;
int wantSum = (sum / 2) + ((sum & 1) == 0 ? 0 : 1);
int[][][] dp = new int[n + 1][k + 1][wantSum + 1];
return f(n, 1, k, wantSum, dp);
}
public static boolean f(int n, int i, int k, int s, int[][][] dp) {
if (k < 0 || s < 0) {
return false;
}
if (i == n + 1) {
return k == 0 && s == 0;
}
if (dp[i][k][s] != 0) {
return dp[i][k][s] == 1;
}
boolean ans = f(n, i + 1, k, s, dp) || f(n, i + 1, k - 1, s - i, dp);
dp[i][k][s] = ans ? 1 : -1;
return ans;
}
// 为了验证
// 对数器
public static void main(String[] args) {
int N = 60;
int testTime = 5000;
System.out.println("测试开始");
for (int i = 0; i < testTime; i++) {
int n = (int) (Math.random() * N) + 2;
int k = (int) (Math.random() * n) + 1;
int[] ans = pick(n, k);
if (!pass(n, k, ans)) {
System.out.println("出错了!");
}
}
System.out.println("测试结束");
}
}
code3 P1439 【模板】最长公共子序列
// 两个排列的最长公共子序列长度
// 给出由1~n这些数字组成的两个排列
// 求它们的最长公共子序列长度
// n <= 10^5
// 测试链接 : https://www.luogu.com.cn/problem/P1439
// 请同学们务必参考如下代码中关于输入、输出的处理
// 这是输入输出处理效率很高的写法
// 提交以下的code,提交时请把类名改成"Main",可以直接通过
如果是字符串的话,是二维动态规划
排列:
求出第二排列在第一个排列的下标数组,
再求出这个下标数组的最长递增子序列
package class087;
// 两个排列的最长公共子序列长度
// 给出由1~n这些数字组成的两个排列
// 求它们的最长公共子序列长度
// n <= 10^5
// 测试链接 : https://www.luogu.com.cn/problem/P1439
// 请同学们务必参考如下代码中关于输入、输出的处理
// 这是输入输出处理效率很高的写法
// 提交以下的code,提交时请把类名改成"Main",可以直接通过
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
public class Code03_PermutationLCS {
public static int MAXN = 100001;
public static int[] a = new int[MAXN];
public static int[] b = new int[MAXN];
public static int[] where = new int[MAXN];
public static int[] ends = new int[MAXN];
public static int n;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StreamTokenizer in = new StreamTokenizer(br);
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
while (in.nextToken() != StreamTokenizer.TT_EOF) {
n = (int) in.nval;
for (int i = 0; i < n; i++) {
in.nextToken();
a[i] = (int) in.nval;
}
for (int i = 0; i < n; i++) {
in.nextToken();
b[i] = (int) in.nval;
}
out.println(compute());
}
out.flush();
out.close();
br.close();
}
public static int compute() {
for (int i = 0; i < n; i++) {
where[a[i]] = i;
}
for (int i = 0; i < n; i++) {
b[i] = where[b[i]];
}
return lis();
}
// 讲解072 - 最长递增子序列及其扩展
public static int lis() {
int len = 0;
for (int i = 0, find; i < n; i++) {
find = bs(len, b[i]);
if (find == -1) {
ends[len++] = b[i];
} else {
ends[find] = b[i];
}
}
return len;
}
public static int bs(int len, int num) {
int l = 0, r = len - 1, m, ans = -1;
while (l <= r) {
m = (l + r) / 2;
if (ends[m] >= num) {
ans = m;
r = m - 1;
} else {
l = m + 1;
}
}
return ans;
}
}
code4 1187. 使数组严格递增
// 使数组严格递增的最小操作数
// 给你两个整数数组 arr1 和 arr2
// 返回使 arr1 严格递增所需要的最小操作数(可能为0)
// 每一步操作中,你可以分别从 arr1 和 arr2 中各选出一个索引
// 分别为 i 和 j,0 <= i < arr1.length 和 0 <= j < arr2.length
// 然后进行赋值运算 arr1[i] = arr2[j]
// 如果无法让 arr1 严格递增,请返回-1
// 1 <= arr1.length, arr2.length <= 2000
// 0 <= arr1[i], arr2[i] <= 10^9
// 测试链接 : https://leetcode.cn/problems/make-array-strictly-increasing/
处理arr2数组,使之变成严格递增不重复的数组
要替换更大的,第一个大选最合适的那个就好了
f(i)
0…i-1是严格递增的,并且i-1是原装的,把0…n-1变成严格递增的
i…后面的数组,要替换多少个
枚举每一个下一个原装位置
那么中间不用原装的数,替换为arr[2]中刚大的那些数
并且要判断可行性原装位置合适吗文章来源:https://www.toymoban.com/news/detail-763721.html
package class087;
import java.util.Arrays;
// 使数组严格递增的最小操作数
// 给你两个整数数组 arr1 和 arr2
// 返回使 arr1 严格递增所需要的最小操作数(可能为0)
// 每一步操作中,你可以分别从 arr1 和 arr2 中各选出一个索引
// 分别为 i 和 j,0 <= i < arr1.length 和 0 <= j < arr2.length
// 然后进行赋值运算 arr1[i] = arr2[j]
// 如果无法让 arr1 严格递增,请返回-1
// 1 <= arr1.length, arr2.length <= 2000
// 0 <= arr1[i], arr2[i] <= 10^9
// 测试链接 : https://leetcode.cn/problems/make-array-strictly-increasing/
public class Code04_MakeArrayStrictlyIncreasing {
public static int makeArrayIncreasing1(int[] arr1, int[] arr2) {
Arrays.sort(arr2);
int m = 1;
for (int i = 1; i < arr2.length; i++) {
if (arr2[i] != arr2[m - 1]) {
arr2[m++] = arr2[i];
}
}
int n = arr1.length;
int[] dp = new int[n];
Arrays.fill(dp, -1);
int ans = f1(arr1, arr2, n, m, 0, dp);
return ans == Integer.MAX_VALUE ? -1 : ans;
}
// arr1长度为n,arr2有效部分长度为m
// arr2有效部分可以替换arr1中的数字
// arr1[0..i-1]已经严格递增且arr1[i-1]一定没有替换
// 返回让arr1整体都严格递增,arr1[i...]范围上还需要几次替换
// 如果做不到,返回无穷大
public static int f1(int[] arr1, int[] arr2, int n, int m, int i, int[] dp) {
if (i == n) {
return 0;
}
if (dp[i] != -1) {
return dp[i];
}
// ans : 遍历所有的分支,所得到的最少的操作次数
int ans = Integer.MAX_VALUE;
// pre : 前一位的数字
int pre = i == 0 ? Integer.MIN_VALUE : arr1[i - 1];
// find : arr2有效长度m的范围上,找到刚比pre大的位置
int find = bs(arr2, m, pre);
// 枚举arr1[i...]范围上,第一个不需要替换的位置j
for (int j = i, k = 0, next; j <= n; j++, k++) {
if (j == n) {
ans = Math.min(ans, k);
} else {
// pre : 被arr2替换的前一位数字
if (pre < arr1[j]) {
next = f1(arr1, arr2, n, m, j + 1, dp);
if (next != Integer.MAX_VALUE) {
ans = Math.min(ans, k + next);
}
}
if (find != -1 && find < m) {
pre = arr2[find++];
} else {
break;
}
}
}
dp[i] = ans;
return ans;
}
// arr2[0..size-1]范围上是严格递增的
// 找到这个范围上>num的最左位置
// 不存在返回-1
public static int bs(int[] arr2, int size, int num) {
int l = 0, r = size - 1, m;
int ans = -1;
while (l <= r) {
m = (l + r) / 2;
if (arr2[m] > num) {
ans = m;
r = m - 1;
} else {
l = m + 1;
}
}
return ans;
}
// 严格位置依赖的动态规划
// 和方法1的思路没有区别
// 甚至填写dp表的逻辑都保持一致
public static int makeArrayIncreasing2(int[] arr1, int[] arr2) {
Arrays.sort(arr2);
int m = 1;
for (int i = 1; i < arr2.length; i++) {
if (arr2[i] != arr2[m - 1]) {
arr2[m++] = arr2[i];
}
}
int n = arr1.length;
int[] dp = new int[n + 1];
for (int i = n - 1, ans, pre, find; i >= 0; i--) {
ans = Integer.MAX_VALUE;
pre = i == 0 ? Integer.MIN_VALUE : arr1[i - 1];
find = bs(arr2, m, pre);
for (int j = i, k = 0, next; j <= n; j++, k++) {
if (j == n) {
ans = Math.min(ans, k);
} else {
if (pre < arr1[j]) {
next = dp[j + 1];
if (next != Integer.MAX_VALUE) {
ans = Math.min(ans, k + next);
}
}
if (find != -1 && find < m) {
pre = arr2[find++];
} else {
break;
}
}
}
dp[i] = ans;
}
return dp[0] == Integer.MAX_VALUE ? -1 : dp[0];
}
}
2023-12-24 16:38:16文章来源地址https://www.toymoban.com/news/detail-763721.html
到了这里,关于class087 动态规划中根据数据量猜解法的技巧【算法】的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!