图用邻接矩阵实现，深度优先遍历和广度优先遍历-Toy模板网

这篇具有很好参考价值的文章主要介绍了图用邻接矩阵实现，深度优先遍历和广度优先遍历。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

邻接矩阵的结构体

#define MAXVertexNum 20//顶点数目最大值
typedef char Vertextype;//顶点的数据类型
typedef int Edgetype;//带权图中边上权值的数据类型
typedef struct
{
	Vertextype Vertex[MAXVertexNum];//顶点表
	Edgetype Edge[MAXVertexNum][MAXVertexNum];//邻接矩阵，边表
	int vernum, arcnum; //图的顶点数和弧数
}MGraph;

邻接矩阵图的建立

图的建立有多种实现方式，我这里是从键盘输入顶点数，边条数，并从键盘输入边的关系

图是带有权值的，并且把环的权值赋值为0，两个顶点没有边权值为32767。

void CreateMGraph(MGraph *G)//图的建立
{
	char cls;//用于清除缓冲区的回车
	int i, j, w, k;
	printf("请输入顶点的数量\n");
	scanf_s("%d", &(G->vernum));
	cls = getchar();//清除缓冲区回车
	printf("请输入边的条数\n");
	scanf_s("%d", &(G->arcnum));
	cls = getchar();
	printf("请输入顶点信息\n");
	for (i = 0; i < G->vernum; i++)//给存储顶点数组赋值
	{
		scanf_s("%c", &(G->Vertex[i]), 1);
	}
	cls = getchar();//清除缓冲区回车
	for (i = 0; i < G->vernum; i++)//初始化边的关系
	{
		for (j = 0; j < G->vernum; j++)
		{
			if (j == i)
			{
				G->Edge[i][j] = 0;//这里我把指向自己的边权值赋值为0
			}
			else
			{
				G->Edge[i][j] = 32767;//指向别人的边赋值为32767
			}
		}
	}
	for (k = 0; k < G->arcnum; k++)//给边赋值
	{
		printf("请输入边的起点序号，终点序号，权值(用空格隔开)：");
		scanf_s("%d%d%d", &i, &j, &w);
		cls = getchar();
		G->Edge[i - 1][j - 1] = w;
		G->Edge[j - 1][i - 1] = w;//无向图具有对称性
	}
}

查找顶点v，并且返回v的相关信息

通过循环去找顶点，如果找到了打印出顶点的位置（节点数组的第几个），并找出与之相连的边，找到了打印出与哪条边相关联，如果想知道权值也可加入

printf("权值为：%d\n",G->Edge[i][j]);

void GetVex(MGraph* G, Vertextype v)//找到顶点v并返回v的相关信息
{
	int i, j;
	for (i = 0; i < G->vernum; i++)
	{
		if (v == G->Vertex[i])
		{
			break;//v存在的话就退出
		}
	}
	if (i == G->vernum)//判断v是否存在
	{
		printf("没找到:%c\n", v);
		return;
	}
	else
	{
		printf("顶点在第：%d个位置\n", i + 1);//打印v在的位置
		for (j = 0; j < G->vernum; j++)
		{
			if (G->Edge[i][j] != 0 && G->Edge[j][i] != 32767)//打印和v存在边关系的vertex[j]
			{
				printf("%c和%c存在边\n", G->Vertex[i], G->Vertex[j]);//打印和v相连的边
			}
		}
	}
}

替换顶点

如你所见代码是将某个顶点替换成某个顶点

void PutVex(MGraph* G, Vertextype v ,Vertextype value)//替换顶点，将v换成value
{
	int i;
	for (i = 0; i < G->vernum; i++)//去边集里面找v
	{
		if (v == G->Vertex[i])
		{
			G->Vertex[i] = value;
			printf("将%c替换%c成功", v, value);
			return;
		}
	}
	if (i == G->vernum)
	{
		printf("没找到:%c\n",v);
	}
}

新增顶点

如你所见代码是在图中新增一个顶点

void InsertVex(MGraph* G, Vertextype v)//新增顶点v
{
	if (G->vernum == MAXVertexNum)
	{
		printf("图满了，存不下了\n");
		return;
	}
	int i, j;
	G->Vertex[G->vernum] = v;
	G->vernum++;
	//初始化和顶点的边
	G->Edge[G->vernum - 1][G->vernum - 1] = 0;
	for (i = 0; i < G->vernum - 1; i++)
	{
		G->Edge[i][G->vernum - 1] = 32767;
		G->Edge[G->vernum - 1][i] = 32767;
	}
	//输入边,G->arcnum（边的数量）要++
	printf("请输入想要与顶点新增的边的序号和权值(输入-1和-1结束)\n");
	while (1)
	{
		scanf_s("%d%d", &j, &i);//用j来表示与之相连的顶点存储位置（下标=位置-1）i来存储权值
		if (j == -1 && i == -1)break; 
		else if (j<1 || j>G->vernum)
		{
			printf("输入错误，请重新输入\n");
			continue;
		}
		G->Edge[G->vernum - 1][j-1] = i;//确定边的关系
		G->Edge[j - 1][G->vernum - 1] = i;
		G->arcnum++;
	}
}

打印矩阵的边的权值

将所有的权值打印出来，直观的表示

void PrintMGraph(MGraph* G)//打印矩阵
{
	int i, j;
	printf("图的矩阵表示为:\n");
	for (i = 0; i < G->vernum; i++)
	{
		for (j = 0; j < G->vernum; j++)
		{
			printf("%d\t", G->Edge[i][j]);//第i行第j列
		}
		printf("\n");
	}
}

深度优先遍历

认真听，认真听，重头戏来了

深度优先遍历，我先用一个visited数组用来保存节点是否被访问，具体代码如下：

/*
深度优先搜索,遍历算法
*/
int visited[MAXVertexNum] = { 0 };//用于记录数组节点是否被访问，访问了就变为1
void DFS(MGraph* G, int i)
{
	visited[i] = 1;//访问过的顶点标记为1
	printf("%c ", G->Vertex[i]);//在进行遍历之前打印访问的顶点
	for (int j = 0; j < G->vernum; j++)//从第0个顶点开始判断，直到最后一个顶点
	{
		if (!visited[j] && G->Edge[i][j] == 1)//若顶点vexs[j]与顶点vexs[i]相连，并且vexs[j]没有访问过
		{
			DFS(G, j);//那就访问vexs[j]
		}
	}
	//printf("%c ", G->Vertex[i]);//如果写在最后，则逆序输出，可以将上面的cout注释掉试一下
}
void DFSTraverseAL(MGraph *G)
{
	for (int i = 0; i < G->vernum; i++) //从vexs[0]开始进行深度优先递归，若是连通图，只会执行一次DFS(G,0)
	{
		if (!visited[i])//判断是否已被访问
		{
			DFS(G, i);
		}
	}
	/*
    //因为深度优先递归后每个visited[i]都是1，不会再执行if了
     //若是非连通图，可能会执行到DFS(G,1)，DFS(G,2)，DFS(G,3)，DFS(G,4)*/
}

广度优先遍历

由于上面没有涉及到队，但是不代表不会用到，在广度优先遍历中，我用队来实现遍历。

因为队这种数据结构，后进后出，很好的切合了广度优先遍历（也就是层次遍历），所以定义了队，话不多说请看代码：

typedef struct LQueueNode//队节点
{
	int data;//队的数据类型
	struct LQueueNode* next;
}LQueueNode;
typedef struct LQueue//队
{
	LQueueNode* front;//队的头指针
	LQueueNode* rear;//尾指针
}LQueue;

void InitLQueue(LQueue* Q)//队的初始化
{
	LQueueNode* p = (LQueueNode*)malloc(sizeof(LQueueNode));
	if (p == NULL)
		exit(-1);
	p->next = NULL;
	Q->front = p;
	Q->rear = p;
}
void PushLQueue(LQueue* Q,int x)//入队操作
{
	LQueueNode* p = (LQueueNode*)malloc(sizeof(LQueueNode));
	if (p == NULL)
		exit(-1);
	p->data = x;
	p->next = NULL;
	Q->rear->next = p;
	Q->rear = p;
}
int PopLQueue(LQueue* Q)//出队操作
{
	if (Q->front->next == NULL)
	{
		printf("队为空\n");
		return -1;
	}
	else
	{
		LQueueNode* r = Q->front->next;
		if (Q->front->next->next == NULL)//如果只有一个元素的话，头删会使得尾指针丢失变为野指针
		{
			Q->rear = Q->front;
		}
		int n = r->data;
		Q->front->next = Q->front->next->next;
		free(r);
		r = NULL;
		return n;
	}
}
int LQueueEmpty(LQueue* Q)//判断队列是否为空
{
	if (Q->front->next == NULL)
		return 0;//空为0
	else
		return 1;//非空为1
}

相信大家已经队这种数据结构已经掌握了，这里就不细说了，请看重头戏：

void BFSraverseAL(MGraph* G)
{
	int i, j;
	for (i = 0; i < G->vernum; i++)//初始化保存标志位的信息
		visited[i] = 0;
	LQueue Q;
	InitLQueue(&Q);
	for (i = 0; i < G->vernum; i++)
	{							   
		if (!visited[i])//未访问过 该顶点
		{
			visited[i] = 1;
			printf("%c ", G->Vertex[i]);
			PushLQueue(&Q, i);
			while (LQueueEmpty(&Q))
			{
				i = PopLQueue(&Q); //将队中元素出队列，赋值给i
				for (j = 0; j < G->vernum; j++)
				{
					if (!visited[j] && G->Edge[i][j])//其他顶点与该顶点存在边
					{
						visited[j] = 1;
						printf("%c ", G->Vertex[j]);
						PushLQueue(&Q, j);
					}
				}
			}
		}
	}
}

完整代码如下：文章来源地址https://www.toymoban.com/news/detail-763763.html

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#pragma warning(disable:6386)//忽略6386错误,（这里我使用的编译器是vs2019不清楚为什么会有6386报错）
#define MAXVertexNum 20//顶点数目最大值
typedef char Vertextype;//顶点的数据类型
typedef int Edgetype;//带权图中边上权值的数据类型
typedef struct
{
	Vertextype Vertex[MAXVertexNum];//顶点表
	Edgetype Edge[MAXVertexNum][MAXVertexNum];//邻接矩阵，边表
	int vernum, arcnum; //图的顶点数和弧数
}MGraph;
typedef struct LQueueNode//队节点
{
	int data;//队的数据类型
	struct LQueueNode* next;
}LQueueNode;
typedef struct LQueue//队
{
	LQueueNode* front;//队的头指针
	LQueueNode* rear;//尾指针
}LQueue;
void CreateMGraph(MGraph *G)//图的建立
{
	char cls;//用于清除缓冲区的回车
	int i, j, w, k;
	printf("请输入顶点的数量\n");
	scanf_s("%d", &(G->vernum));
	cls = getchar();//清除缓冲区回车
	printf("请输入边的条数\n");
	scanf_s("%d", &(G->arcnum));
	cls = getchar();
	printf("请输入顶点信息\n");
	for (i = 0; i < G->vernum; i++)//给存储顶点数组赋值
	{
		scanf_s("%c", &(G->Vertex[i]), 1);
	}
	cls = getchar();//清除缓冲区回车
	for (i = 0; i < G->vernum; i++)//初始化边的关系
	{
		for (j = 0; j < G->vernum; j++)
		{
			if (j == i)
			{
				G->Edge[i][j] = 0;//这里我把指向自己的边权值赋值为0
			}
			else
			{
				G->Edge[i][j] = 32767;//指向别人的边赋值为32767
			}
		}
	}
	for (k = 0; k < G->arcnum; k++)//给边赋值
	{
		printf("请输入边的起点序号，终点序号，权值(用空格隔开)：");
		scanf_s("%d%d%d", &i, &j, &w);
		cls = getchar();
		G->Edge[i - 1][j - 1] = w;
		G->Edge[j - 1][i - 1] = w;//无向图具有对称性
	}
}
void GetVex(MGraph* G, Vertextype v)//找到顶点v并返回v的相关信息
{
	int i, j;
	for (i = 0; i < G->vernum; i++)
	{
		if (v == G->Vertex[i])
		{
			break;//v存在的话就退出
		}
	}
	if (i == G->vernum)//判断v是否存在
	{
		printf("没找到:%c\n", v);
		return;
	}
	else
	{
		printf("顶点在第：%d个位置\n", i + 1);//打印v在的位置
		for (j = 0; j < G->vernum; j++)
		{
			if (G->Edge[i][j] != 0 && G->Edge[j][i] != 32767)//打印和v存在边关系的vertex[j]
			{
				printf("%c和%c存在边\n", G->Vertex[i], G->Vertex[j]);//打印和v相连的边
			}
		}
	}
}

void PutVex(MGraph* G, Vertextype v ,Vertextype value)//替换顶点，将v换成value
{
	int i;
	for (i = 0; i < G->vernum; i++)//去边集里面找v
	{
		if (v == G->Vertex[i])
		{
			G->Vertex[i] = value;
			printf("将%c替换%c成功", v, value);
			return;
		}
	}
	if (i == G->vernum)
	{
		printf("没找到:%c\n",v);
	}
}

void InsertVex(MGraph* G, Vertextype v)//新增顶点v
{
	if (G->vernum == MAXVertexNum)
	{
		printf("图满了，存不下了\n");
		return;
	}
	int i, j;
	G->Vertex[G->vernum] = v;
	G->vernum++;
	//初始化和顶点的边
	G->Edge[G->vernum - 1][G->vernum - 1] = 0;
	for (i = 0; i < G->vernum - 1; i++)
	{
		G->Edge[i][G->vernum - 1] = 32767;
		G->Edge[G->vernum - 1][i] = 32767;
	}
	//输入边,G->arcnum（边的数量）要++
	printf("请输入想要与顶点新增的边的序号和权值(输入-1和-1结束)\n");
	while (1)
	{
		scanf_s("%d%d", &j, &i);//用j来表示与之相连的顶点存储位置（下标=位置-1）i来存储权值
		if (j == -1 && i == -1)break; 
		else if (j<1 || j>G->vernum)
		{
			printf("输入错误，请重新输入\n");
			continue;
		}
		G->Edge[G->vernum - 1][j-1] = i;//确定边的关系
		G->Edge[j - 1][G->vernum - 1] = i;
		G->arcnum++;
	}
}
void PrintMGraph(MGraph* G)//打印矩阵
{
	int i, j;
	printf("图的矩阵表示为:\n");
	for (i = 0; i < G->vernum; i++)
	{
		for (j = 0; j < G->vernum; j++)
		{
			printf("%d\t", G->Edge[i][j]);//第i行第j列
		}
		printf("\n");
	}
}
/*
深度优先搜索,遍历算法
*/
int visited[MAXVertexNum] = { 0 };//用于记录数组节点是否被访问，访问了就变为1
void DFS(MGraph* G, int i)
{
	visited[i] = 1;//访问过的顶点标记为1
	printf("%c ", G->Vertex[i]);//在进行遍历之前打印访问的顶点
	for (int j = 0; j < G->vernum; j++)//从第0个顶点开始判断，直到最后一个顶点
	{
		if (!visited[j] && G->Edge[i][j] == 1)//若顶点vexs[j]与顶点vexs[i]相连，并且vexs[j]没有访问过
		{
			DFS(G, j);//那就访问vexs[j]
		}
	}
	//printf("%c ", G->Vertex[i]);//如果写在最后，则逆序输出，可以将上面的cout注释掉试一下
}
void DFSTraverseAL(MGraph *G)
{
	for (int i = 0; i < G->vernum; i++) //从vexs[0]开始进行深度优先递归，若是连通图，只会执行一次DFS(G,0)
	{
		if (!visited[i])//判断是否已被访问
		{
			DFS(G, i);
		}
	}
	/*
    //因为深度优先递归后每个visited[i]都是1，不会再执行if了
     //若是非连通图，可能会执行到DFS(G,1)，DFS(G,2)，DFS(G,3)，DFS(G,4)*/
}
void InitLQueue(LQueue* Q)//队的初始化
{
	LQueueNode* p = (LQueueNode*)malloc(sizeof(LQueueNode));
	if (p == NULL)
		exit(-1);
	p->next = NULL;
	Q->front = p;
	Q->rear = p;
}
void PushLQueue(LQueue* Q,int x)//入队操作
{
	LQueueNode* p = (LQueueNode*)malloc(sizeof(LQueueNode));
	if (p == NULL)
		exit(-1);
	p->data = x;
	p->next = NULL;
	Q->rear->next = p;
	Q->rear = p;
}
int PopLQueue(LQueue* Q)//出队操作
{
	if (Q->front->next == NULL)
	{
		printf("队为空\n");
		return -1;
	}
	else
	{
		LQueueNode* r = Q->front->next;
		if (Q->front->next->next == NULL)//如果只有一个元素的话，头删会使得尾指针丢失变为野指针
		{
			Q->rear = Q->front;
		}
		int n = r->data;
		Q->front->next = Q->front->next->next;
		free(r);
		r = NULL;
		return n;
	}
}
int LQueueEmpty(LQueue* Q)//判断队列是否为空
{
	if (Q->front->next == NULL)
		return 0;//空为0
	else
		return 1;//非空为1
}

void BFSraverseAL(MGraph* G)
{
	int i, j;
	for (i = 0; i < G->vernum; i++)//初始化保存标志位的信息
		visited[i] = 0;
	LQueue Q;
	InitLQueue(&Q);
	for (i = 0; i < G->vernum; i++)
	{							  
		if (!visited[i])//未访问过 该顶点
		{
			visited[i] = 1;
			printf("%c ", G->Vertex[i]);
			PushLQueue(&Q, i);
			while (LQueueEmpty(&Q))
			{
				i = PopLQueue(&Q); //将队中元素出队列，赋值给i
				for (j = 0; j < G->vernum; j++)
				{
					if (!visited[j] && G->Edge[i][j])//其他顶点与该顶点存在边
					{
						visited[j] = 1;
						printf("%c ", G->Vertex[j]);
						PushLQueue(&Q, j);
					}
				}
			}
		}
	}
}
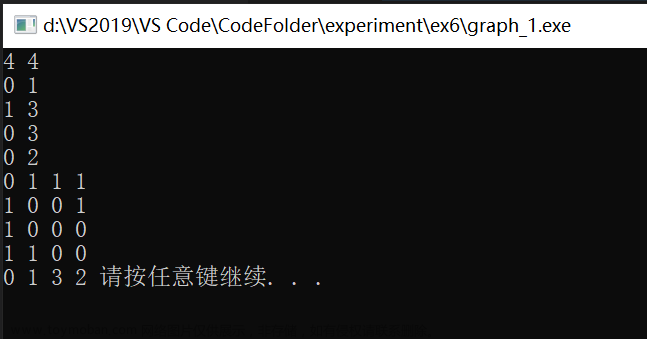
/*//一组数据
4
4
ABCD
1 2 1
1 3 1
2 3 1
3 4 1


*/
int main()
{
	MGraph G;
	CreateMGraph(&G);//图的建立
	//GetVex(&G, 'A'); //找到顶点A并返回A的相关信息
	//PutVex(&G, 'A', 'a');//替换顶点，将A换成a
	//InsertVex(&G, 'D');//新增顶点函数
	DFSTraverseAL(&G);
	printf("\n");
	BFSraverseAL(&G);
	printf("\n");
	PrintMGraph(&G);//矩阵的打印
	return 0;
}

到了这里，关于图用邻接矩阵实现，深度优先遍历和广度优先遍历的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！