一、数据结构定义
1、图
#define MaxVertexNum 100 // 最大可存储的节点数目
/*图*/
typedef char VexterType;
typedef int EdgeType;
typedef struct GraphMatrix {
VexterType Vexs[MaxVertexNum]; //结点
EdgeType Edges[MaxVertexNum][MaxVertexNum]; //边
int vexnum, arcnum; //当前点数和边数
}*MGraph;
int visited[MaxVertexNum]; // 记录是否访问该节点,访问过为1,否则为0使用邻接矩阵法存储图的信息,其中
- 一维矩阵 Vexs[] 存储节点信息
- 二维矩阵 Edges[][] 存储边的信息
- 一维矩阵 visited[] 记录当前节点是否被访问过,用于后面的遍历
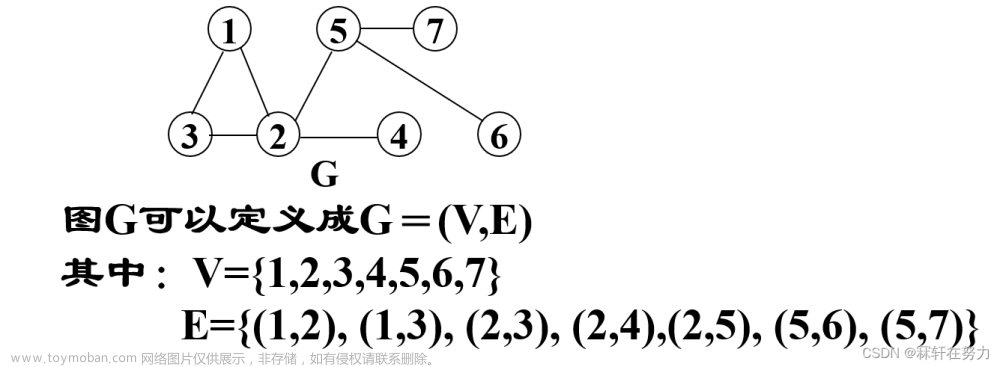
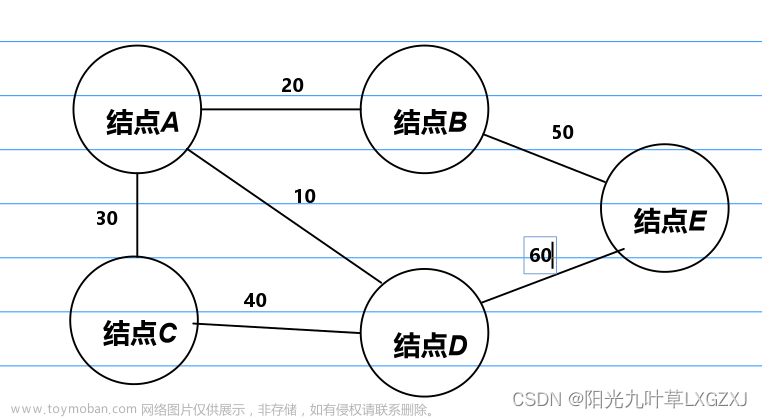
本文所使用的图的结构如下:
对应的 Vexs[] 为:A,B,C,D,E,F(对应的数组下标从0到5)
对应的 Edges[][] 如下:
2、队列
/*队列*/
typedef int QueueType;
typedef struct QueueNode {
QueueType data;
struct QueueNode* next;
}QueueNode;
typedef struct {
QueueNode* front, * rear;
}LinkQueue;图的广度优先遍历BFS需要使用队列进行辅助
二、方法概览
1、队列
void initQueue(LinkQueue* Q);//初始化队列
int isQueueEmpty(LinkQueue* Q);//判断队列是否为空
void enQueue(LinkQueue* Q, QueueType data);//入队
int deQueue(LinkQueue* Q, QueueType* data);//出队2、图
void printGraph(MGraph G);//打印图的邻接矩阵
MGraph initGraph();//初始化图并输入数据
int adjacent(MGraph G, int x, int y);//判断是否存在某条边(x,y)
int firstNeighbor(MGraph G, int v);//求点v的第一个邻接点
int nextNeighbor(MGraph G, int v, int w);//求点v的邻接点w的下一个邻接点
void visit(MGraph G, int v);//访问该节点的信息
void BFS(MGraph G, LinkQueue Q, int v);// 广度优先遍历
void BFSTraverse(MGraph G);//广度优先遍历 主函数
void DFS(MGraph G, int v);//深度优先遍历
void DFSTraverse(MGraph G);//深度优先遍历 主函数三、方法详解
1、队列
//初始化队列
void initQueue(LinkQueue* Q) {
Q->front = Q->rear = (QueueNode*)malloc(sizeof(QueueNode)); // 分配头节点
Q->front->next = NULL; //初始化为空
}
//判断队列是否为空
int isQueueEmpty(LinkQueue* Q) {
if (Q->front == Q->rear) return 1;
else return 0;
}
//入队
void enQueue(LinkQueue* Q, QueueType data) {
QueueNode* news = (QueueNode*)malloc(sizeof(QueueNode));
news->data = data; // 创建新节点,插入队列尾部
news->next = NULL;
Q->rear->next = news;
Q->rear = news;
}
//出队
int deQueue(LinkQueue* Q, QueueType* data) {
if (Q->front == Q->rear) return 0;
QueueNode* del = Q->front->next;
*data = del->data;
Q->front->next = del->next;
if (Q->rear == del)
Q->rear = Q->front; // 若原队列只有一个节点,删除后变空
free(del);
return 1;
}2、图
(1)基本操作
// 打印图的邻接矩阵
void printGraph(MGraph G) {
int i, j;
printf("G->Edges[][] = \n\t");
for (i = 0; i < G->vexnum; ++i)
printf(" %c \t", G->Vexs[i]);
printf("\n");
for (i = 0; i < G->vexnum; ++i) {
printf(" %c \t", G->Vexs[i]);
for (j = 0; j < G->vexnum; j++)
printf(" %d \t", G->Edges[i][j]);
printf("\n");
}
}
// 初始化图并输入数据
MGraph initGraph() {
int i, j;
MGraph G = (MGraph)malloc(sizeof(struct GraphMatrix));
G->vexnum = 6;
G->arcnum = 14;
/* 初始化图的邻接矩阵 Edges[MaxVertexNum][MaxVertexNum] */
for (i = 0; i < G->vexnum; i++) {
for (j = 0; j < G->vexnum; j++) {
G->Edges[i][j] = 0;
}
}
/* 输入图的结点矩阵 Vexs[MaxVertexNum] */
int v[6] = { 'A','B','C','D','E','F' };
for (i = 0; i < G->vexnum; i++)
G->Vexs[i] = v[i];
/* 输入图的边权 */
int start_vex[14] = { 0,0,0,1,1,1,2,2,3,3,4,4,5,5 };
int end_vex[14] = { 1,2,3,0,4,5,0,1,0,5,1,2,1,3 };
for (i = 0; i < G->arcnum; i++)
G->Edges[start_vex[i]][end_vex[i]] = 1;
return G;
}
// 判断是否存在某条边(x,y)
int adjacent(MGraph G, int x, int y) {
if (G->Edges[x][y] == 1)
return 1;
else
return -1;
}
// 求点v的第一个邻接点
// 若有返回顶点号,否则返回-1
int firstNeighbor(MGraph G, int v) {
for (int i = 0; i < G->Vexs; i++) {
if (G->Edges[v][i] == 1)
return i;
}
return -1;
}
// 求点v的邻接点w的下一个邻接点
// 若有返回顶点号,否则返回-1
int nextNeighbor(MGraph G, int v, int w) {
if (w < G->vexnum) {
for (int i = w + 1; i < G->vexnum; i++) {
if (G->Edges[v][i] == 1)
return i;
}
return -1;
}
return -1;
}(2)图的深度优先遍历DFS
// 访问该节点的信息
void visit(MGraph G,int v) {
printf("%c ",G->Vexs[v]);
}
// 深度优先遍历
void DFS(MGraph G, int v) {
visit(G, v);
visited[v] = 1;
for (int w = firstNeighbor(G, v); w >= 0; w = nextNeighbor(G, v, w)) {
if (visited[w] == 0)
DFS(G, w);
}
}
// 深度优先遍历 主函数
void DFSTraverse(MGraph G) {
for (int i = 0; i < G->vexnum; ++i) {
visited[i] = 0;
}
for (int i = 0; i < G->vexnum; ++i) {
if (visited[i] == 0)
DFS(G, i);
}
}(3)图的广度优先遍历BFS
// 访问该节点的信息
void visit(MGraph G,int v) {
printf("%c ",G->Vexs[v]);
}
// 广度优先遍历
void BFS(MGraph G, LinkQueue Q, int v) {
visit(G, v);
visited[v] = 1;
enQueue(&Q, v);
while (!isQueueEmpty(&Q)) {
deQueue(&Q, &v);
for (int w = firstNeighbor(G, v); w >= 0; w = nextNeighbor(G, v, w)) {
if (visited[w] == 0) {
visit(G, w);
visited[w] = 1;
enQueue(&Q, w);
}
}
}
}
// 广度优先遍历 主函数
void BFSTraverse(MGraph G) {
for (int i = 0; i < G->vexnum; ++i) {
visited[i] = 0;
}
LinkQueue Q;
initQueue(&Q);
for (int i = 0; i < G->vexnum; ++i) {
if (visited[i] == 0)
BFS(G, Q, i);
}
}
四、运行结果
main方法代码如下:
int main() {
MGraph G = initGraph();
printGraph(G);
printf("\n广度优先遍历 : ");
BFSTraverse(G);
printf("\n深度优先遍历 : ");
DFSTraverse(G);
return 0;
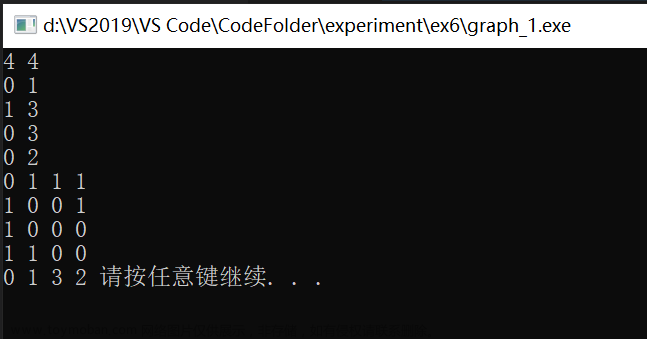
}运行结果如下:文章来源:https://www.toymoban.com/news/detail-764045.html
 文章来源地址https://www.toymoban.com/news/detail-764045.html
文章来源地址https://www.toymoban.com/news/detail-764045.html
五、源代码
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#define MaxVertexNum 100 // 最大可存储的节点数目
/*图*/
typedef char VexterType;
typedef int EdgeType;
typedef struct GraphMatrix {
VexterType Vexs[MaxVertexNum]; //结点
EdgeType Edges[MaxVertexNum][MaxVertexNum]; //边
int vexnum, arcnum; //当前点数和边数
}*MGraph;
int visited[MaxVertexNum]; // 记录是否访问该节点,访问过为1,否则为0
/*队列*/
typedef int QueueType;
typedef struct QueueNode {
QueueType data;
struct QueueNode* next;
}QueueNode;
typedef struct {
QueueNode* front, * rear;
}LinkQueue;
void initQueue(LinkQueue* Q);//初始化队列
int isQueueEmpty(LinkQueue* Q);//判断队列是否为空
void enQueue(LinkQueue* Q, QueueType data);//入队
int deQueue(LinkQueue* Q, QueueType* data);//出队
void printGraph(MGraph G);//打印图的邻接矩阵
MGraph initGraph();//初始化图并输入数据
int adjacent(MGraph G, int x, int y);//判断是否存在某条边(x,y)
int firstNeighbor(MGraph G, int v);//求点v的第一个邻接点
int nextNeighbor(MGraph G, int v, int w);//求点v的邻接点w的下一个邻接点
void visit(MGraph G, int v);//访问该节点的信息
void BFS(MGraph G, LinkQueue Q, int v);// 广度优先遍历
void BFSTraverse(MGraph G);//广度优先遍历 主函数
void DFS(MGraph G, int v);//深度优先遍历
void DFSTraverse(MGraph G);//深度优先遍历 主函数
//初始化队列
void initQueue(LinkQueue* Q) {
Q->front = Q->rear = (QueueNode*)malloc(sizeof(QueueNode)); // 分配头节点
Q->front->next = NULL; //初始化为空
}
//判断队列是否为空
int isQueueEmpty(LinkQueue* Q) {
if (Q->front == Q->rear) return 1;
else return 0;
}
//入队
void enQueue(LinkQueue* Q, QueueType data) {
QueueNode* news = (QueueNode*)malloc(sizeof(QueueNode));
news->data = data; // 创建新节点,插入队列尾部
news->next = NULL;
Q->rear->next = news;
Q->rear = news;
}
//出队
int deQueue(LinkQueue* Q, QueueType* data) {
if (Q->front == Q->rear) return 0;
QueueNode* del = Q->front->next;
*data = del->data;
Q->front->next = del->next;
if (Q->rear == del)
Q->rear = Q->front; // 若原队列只有一个节点,删除后变空
free(del);
return 1;
}
// 打印图的邻接矩阵
void printGraph(MGraph G) {
int i, j;
printf("G->Edges[][] = \n\t");
for (i = 0; i < G->vexnum; ++i)
printf(" %c \t", G->Vexs[i]);
printf("\n");
for (i = 0; i < G->vexnum; ++i) {
printf(" %c \t", G->Vexs[i]);
for (j = 0; j < G->vexnum; j++)
printf(" %d \t", G->Edges[i][j]);
printf("\n");
}
}
// 初始化图并输入数据
MGraph initGraph() {
int i, j;
MGraph G = (MGraph)malloc(sizeof(struct GraphMatrix));
G->vexnum = 6;
G->arcnum = 14;
/* 初始化图的邻接矩阵 Edges[MaxVertexNum][MaxVertexNum] */
for (i = 0; i < G->vexnum; i++) {
for (j = 0; j < G->vexnum; j++) {
G->Edges[i][j] = 0;
}
}
/* 输入图的结点矩阵 Vexs[MaxVertexNum] */
int v[6] = { 'A','B','C','D','E','F' };
for (i = 0; i < G->vexnum; i++)
G->Vexs[i] = v[i];
/* 输入图的边权 */
int start_vex[14] = { 0,0,0,1,1,1,2,2,3,3,4,4,5,5 };
int end_vex[14] = { 1,2,3,0,4,5,0,1,0,5,1,2,1,3 };
for (i = 0; i < G->arcnum; i++)
G->Edges[start_vex[i]][end_vex[i]] = 1;
return G;
}
// 判断是否存在某条边(x,y)
int adjacent(MGraph G, int x, int y) {
if (G->Edges[x][y] == 1)
return 1;
else
return -1;
}
// 求点v的第一个邻接点
// 若有返回顶点号,否则返回-1
int firstNeighbor(MGraph G, int v) {
for (int i = 0; i < G->vexnum; i++) {
if (G->Edges[v][i] == 1)
return i;
}
return -1;
}
// 求点v的邻接点w的下一个邻接点
// 若有返回顶点号,否则返回-1
int nextNeighbor(MGraph G, int v, int w) {
if (w < G->vexnum) {
for (int i = w + 1; i < G->vexnum; i++) {
if (G->Edges[v][i] == 1)
return i;
}
return -1;
}
return -1;
}
// 访问该节点的信息
void visit(MGraph G,int v) {
printf("%c ",G->Vexs[v]);
}
// 广度优先遍历
void BFS(MGraph G, LinkQueue Q, int v) {
visit(G, v);
visited[v] = 1;
enQueue(&Q, v);
while (!isQueueEmpty(&Q)) {
deQueue(&Q, &v);
for (int w = firstNeighbor(G, v); w >= 0; w = nextNeighbor(G, v, w)) {
if (visited[w] == 0) {
visit(G, w);
visited[w] = 1;
enQueue(&Q, w);
}
}
}
}
// 广度优先遍历 主函数
void BFSTraverse(MGraph G) {
for (int i = 0; i < G->vexnum; ++i) {
visited[i] = 0;
}
LinkQueue Q;
initQueue(&Q);
for (int i = 0; i < G->vexnum; ++i) {
if (visited[i] == 0)
BFS(G, Q, i);
}
}
// 深度优先遍历
void DFS(MGraph G, int v) {
visit(G, v);
visited[v] = 1;
for (int w = firstNeighbor(G, v); w >= 0; w = nextNeighbor(G, v, w)) {
if (visited[w] == 0)
DFS(G, w);
}
}
// 深度优先遍历 主函数
void DFSTraverse(MGraph G) {
for (int i = 0; i < G->vexnum; ++i) {
visited[i] = 0;
}
for (int i = 0; i < G->vexnum; ++i) {
if (visited[i] == 0)
DFS(G, i);
}
}
int main() {
MGraph G = initGraph();
printGraph(G);
printf("\n广度优先遍历 : ");
BFSTraverse(G);
printf("\n深度优先遍历 : ");
DFSTraverse(G);
return 0;
}
到了这里,关于数据结构 | 图的遍历的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!