1. Toy模板网首页
  2. > Toy博客

数据结构，第8章：排序(复习）

9月前 作者：Landing_on_Mars 分类：Toy博客 阅读(29) 违法举报

这篇具有很好参考价值的文章主要介绍了数据结构，第8章：排序(复习）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

目录

直接插入排序：

1. (程序题)

折半插入排序：

希尔排序：

3. (程序题)

冒泡排序 ：

2. (程序题)

快速排序 ：

5. (程序题)

 简单选择排序：

4. (程序题)

堆排序：

6. (程序题)

前置知识： 

稳定排序：如果有两个相等的元素在排序前后的相对顺序保持不变，那么排序算法是稳定的。

直接插入排序：

直接插入排序（Insertion Sort）是一种简单直观的排序算法，其基本思想是将待排序的序列分成两部分，已排序部分和未排序部分。初始时，已排序部分只包含第一个元素，然后从未排序部分取出元素，插入到已排序部分的适当位置，使得已排序部分仍然有序。重复这个过程，直到未排序部分为空。

基本思想：排序方法中,从未排序序列中依次取出元素与已排序序列中的元素进行比较,将其放入已排序序列的正确位置上。

1. (程序题)

试设计算法实现直接插入排序,输出在第m趟排序后的结果

输入数据两行：

第1行：多个需要排序的整数，以0结束

第2行：数m，表示第几趟的插入算法

输入：

2 5 3 4 8 7 9 6 1 0

5
输出：
2 3 4 5 7 8 9 6 1 

#include <iostream>
#include <string>
#include <cstring>
#include <cmath>
#include <ctime>
#include <algorithm>
#include <utility>
#include <stack>
#include <queue>
#include <vector>
#include <set>
#include <math.h>
#include <map>
#include <sstream>
#include <deque>
#include <unordered_map>

using namespace std;
typedef long long LL;
const int N = 1e4;

int ar[N];
int n;

// 插入排序函数
void sort(int m) {
    for (int i = 2; i <= n && m; i++) {
        m--;
        if (ar[i - 1] > ar[i]) {
            ar[0] = ar[i];
            int j;
            for (j = i - 1; j > 0 && ar[0] < ar[j]; j--)
                ar[j + 1] = ar[j];
            ar[j + 1] = ar[0];
        }
    }
}

int main() {
    do {
        cin >> ar[++n];
    } while (ar[n]);
    n--; 
    int m;
    cin >> m;
    //m = n - 1;
    sort(m);
    for (int i = 1; i <= n; i++) {
        cout << ar[i] << " ";
    }
    return 0;
}

用例1：

输入

2 5 3 4 8 7 9 6 1 0 5

输出

2 3 4 5 7 8 9 6 1

用例2：

输入

2 5 3 1 6 10 19 4 18 22 0 6

输出

1 2 3 5 6 10 19 4 18 22

折半插入排序：

折半插入排序是在直接插入排序的基础上的改进，使用二分查找确定插入的位置，虽然移动的次数不变，但是查找的效率得到了明显的提升。

#include <iostream>
#include <string>
#include <cstring>
#include <cmath>
#include <ctime>
#include <algorithm>
#include <utility>
#include <stack>
#include <queue>
#include <vector>
#include <set>
#include <math.h>
#include <map>
#include <sstream>
#include <deque>
#include <unordered_map>

using namespace std;
typedef long long LL;
const int N = 1e4;

int ar[N];
int n;

// 插入排序函数
void sort() {
    for (int i = 2; i <= n ; i++) {
        if (ar[i - 1] > ar[i]) {
            ar[0] = ar[i];
            int j;
            int l = 1, r = i-1, mid, ret = 1;
            while (l <= r) {
                mid = l + (r - l) / 2;
                if (ar[mid]<=ar[0]) {
                    l = mid + 1;
                }
                else {
                    r = mid - 1;
                    ret = mid;
                }
            }
            for (j = i - 1; j >= ret ; j--)
                ar[j + 1] = ar[j];
            ar[ret] = ar[0];
        }
    }
}

int main() {
    do {
        cin >> ar[++n];
    } while (ar[n]);
    n--;
    sort();
    for (int i = 1; i <= n; i++) {
        cout << ar[i] << " ";
    }
    return 0;
}

希尔排序：

希尔排序也是出入排序的一种改进版，通过固定的距离的跳跃取数将序列分为多组，每组内进行插入排序，最终实现序列的排序。 不难看出，简单插入排序就是间距为1的希尔排序。

希尔排序的时间复杂度是一个很难求解的问题，但大量的实验和研究表明，当增量序列为 dt[k]=2^(t-k+1)-1 时，时间复杂度为 O(n^(3/2)),其中 t 为排序趟数，1<=k<=t<=log2(n+1），当 n 趋向与无穷时 复杂度可以为 O（n(log2(n))^2)。

3. (程序题)

试编写算法，实现希尔排序。

输出在第m趟排序后的结果

输入数据两行：

第1行：多个需要排序的整数，以0结束

第2行：数m，表示第几趟的希尔排序算法

增量序列统一取【5，3，1】

输入：

1 8 4 6 7 9 5 3 2 11 0

1

输出：
1 5 3 2 7 9 8 4 6 11

#include <iostream>
#include <string>
#include <cstring>
#include <cmath>
#include <ctime>
#include <algorithm>
#include <utility>
#include <stack>
#include <queue>
#include <vector>
#include <set>
#include <math.h>
#include <map>
#include <sstream>
#include <deque>
#include <unordered_map>

using namespace std;

typedef long long LL;
const int N = 1e4;

int n;
int ar[N], d[3] = {5, 3, 1};

void F(int u) {
    for (int i = 1 + u; i <= n; i++) {
        if (ar[i] < ar[i - u]) {
            ar[0] = ar[i];
            int j;
            for (j = i - u; j > 0 && ar[0] < ar[j]; j -= u)
                ar[j + u] = ar[j];
            ar[j + u] = ar[0];
        }
    }
}

void sort(int m) {
    for (int i = 0; i < 3 && i < m; i++) {
        F(d[i]);
    }
}

int main() {
    do {
        cin >> ar[++n];
    } while (ar[n]);
    n--;
    int m;
    cin >> m;
    sort(m);
    for (int i = 1; i <= n; i++) {
        cout << ar[i] << " ";
    }
    return 0;
}

输入

3 15 9 15 10 4 8 12 20 13 0 2

输出

3 8 4 13 10 9 15 12 20 15

输入

1 8 4 6 7 9 5 3 2 11 0 1

输出

1 5 3 2 7 9 8 4 6 11

输入

100 81 4 66 7 9 55 3 2 11 9 0 3

输出

2 3 4 7 9 9 11 55 66 81 100

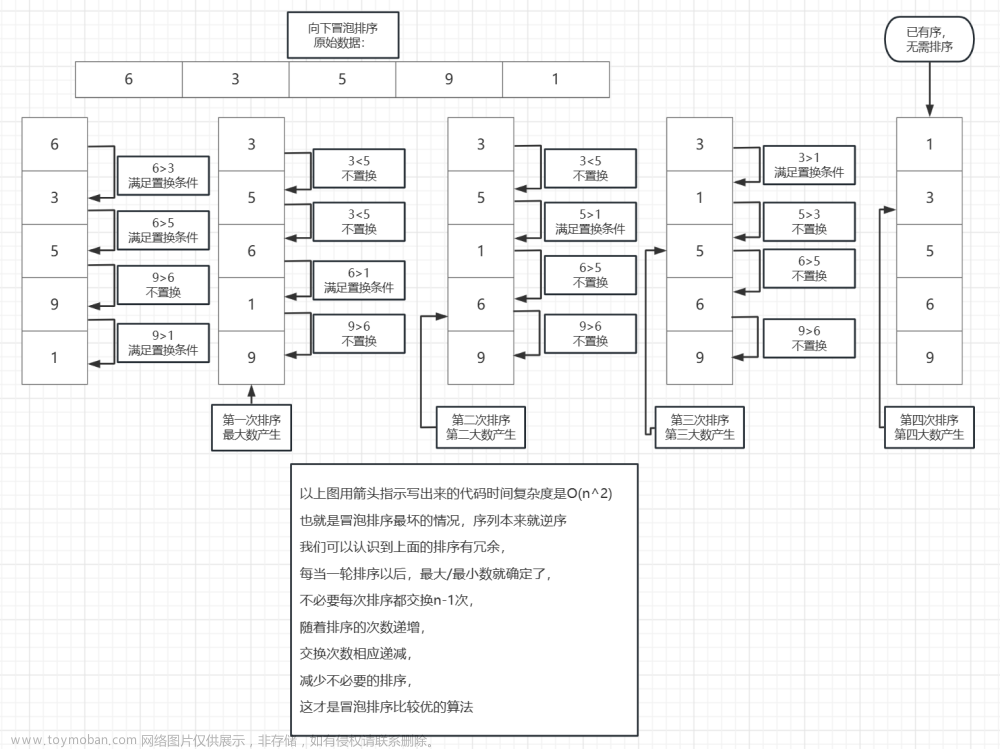
冒泡排序 ：

冒泡排序（Bubble Sort）是一种简单的排序算法，它重复地遍历待排序数组，一次比较两个元素，如果它们的顺序错误就交换它们。遍历数组的工作是重复地进行直到没有再需要交换，也就是数组已经排序完成。

基本思想：排序时扫描待排序记录序列,顺次比较相邻的两个元素的大小,逆序时就交换位置。

2. (程序题)

试设计算法实现冒泡排序。输出在第m趟排序后的结果

输入数据两行：

第1行：多个需要排序的整数，以0结束

第2行：数m，表示第几趟后的冒泡算法

输入：
2 4 3 9 6 8 7 5 1 0

3
输出：
2 3 4 6 5 1 7 8 9 

#include <iostream>
#include <string>
#include <cstring>
#include <cmath>
#include <ctime>
#include <algorithm>
#include <utility>
#include <stack>
#include <queue>
#include <vector>
#include <set>
#include <math.h>
#include <map>
#include <sstream>
#include <deque>
#include <unordered_map>

using namespace std;

typedef long long LL;
const int N = 1e4;

int ar[N];
int n;

void sort(int m) {
    for (int i = 1, flg = 0; i <= m; i++, flg = 0) {
        for (int j = 1; j <= n - i; j++) {
            if (ar[j] > ar[j + 1]) {
                flg = 1;
                ar[0] = ar[j];
                ar[j] = ar[j + 1];
                ar[j + 1] = ar[0];
            }
        }
        if (flg == 0)
            break;
    }
}

int main() {
    do {
        cin >> ar[++n];
    } while (ar[n]);
    n--;
    int m;
    cin >> m;
    sort(m);
    for (int i = 1; i <= n; i++) {
        cout << ar[i] << " ";
    }
    return 0;
}

输入

2 4 3 9 6 8 7 5 1 0 3

输出

2 3 4 6 5 1 7 8 9

输入

3 15 9 15 10 4 8 12 0 4

输出

3 4 8 9 10 12 15 15

快速排序 ：

快速排序是由冒泡排序改进而得。在冒泡排序中，只对相邻的两个记录进行比较，因此每次交换两个相邻记录时只能消除一个逆序。如果能通过两个（不相邻）的记录的一次交换，消除多个逆序，则会大大加快排序的速度。快速排序方法中的一次交换可消除多个逆序。

算法步骤：

选择一个数，通常为第一个，通过交换排序将比这个数大的放到右边，比这个数小的放到左边，然后再使用递归方法，同样的处理两边的数，知道所有的数都有序。

平均时间复杂度O(nlog2(n))

不难发现快速排序的递归过程是一棵二叉树

快速排序（Quick Sort）是一种基于分治思想的排序算法。它选择一个基准元素，将数组分为两个子数组，使得左边的元素都小于基准元素，右边的元素都大于基准元素。然后递归地对左右子数组进行排序。快速排序是一种高效的排序算法，其平均时间复杂度为 O(n log n)。

5. (程序题)

试编写算法实现快速排序算法。

输入：
1 8 4 6 7 9 5 3 2 0
输出：
1 2 3 4 5 6 7 8 9

#include <iostream>
#include <string>
#include <cstring>
#include <cmath>
#include <ctime>
#include <algorithm>
#include <utility>
#include <stack>
#include <queue>
#include <vector>
#include <set>
#include <math.h>
#include <map>
#include <sstream>
#include <deque>
#include <unordered_map>
using namespace std;
typedef long long LL;
const int N = 1e4;
int n;
int ar[N];
void sort(int L, int R) {
    if (L >= R)
        return;
    int t = ar[L];
    int l = L, r = R;
    while (l < r) {
        while (ar[r] >= t && l < r) {
            r--;
        }
        if (ar[r] < t)
            ar[l] = ar[r];
        while (ar[l] <= t && l < r) {
            l++;
        }
        if (ar[l] > t)
            ar[r] = ar[l];
    }
    ar[l] = t;
    sort(L, l - 1);
    sort(l + 1, R);
}

int main() {
    do {
        cin >> ar[++n];
    } while (ar[n]);
    n--;
    sort(1, n);
    for (int i = 1; i <= n; i++) {
        cout << ar[i] << " ";
    }
    return 0;
}

输入

1 8 4 6 7 9 5 3 2 0

输出

1 2 3 4 5 6 7 8 9

输入

9 15 3 15 10 4 8 12 0

输出

3 4 8 9 10 12 15 15

 简单选择排序：

算法思路：

依次选出最小、第二小、第三小……最大的数，存入对应的位置。

4. (程序题)

试设计算法实现简单选择排序。

输出在第m趟排序后的结果

输入数据两行：

第1行：多个需要排序的整数，以0结束

第2行：数m，表示第几趟的排序

输入：
1 8 4 6 7 9 5 3 2 0

3
输出：
1 2 3 6 7 9 5 4 8 

#include <iostream>
#include <string>
#include <cstring>
#include <cmath>
#include <ctime>
#include <algorithm>
#include <utility>
#include <stack>
#include <queue>
#include <vector>
#include <set>
#include <math.h>
#include <map>
#include <sstream>
#include <deque>
#include <unordered_map>
using namespace std;
typedef long long LL;
const int N = 1e4;
int n;
int ar[N], d[3] = { 5, 3, 1 };
void sort(int m) {
    for (int i = 1; i < n && m; i++) {
        m--;
        int mn = i;
        for (int j = i; j <= n; j++) {
            if (ar[j] < ar[mn]) {
                mn = j;
            }
        }
        ar[0] = ar[i];
        ar[i] = ar[mn];
        ar[mn] = ar[0];
    }
}

int main() {
    do {
        cin >> ar[++n];
    } while (ar[n]);
    n--;
    int m;
    cin >> m;
    sort(m);
    for (int i = 1; i <= n; i++) {
        cout << ar[i] << " ";
    }
    return 0;
}

输入

1 8 4 6 7 9 5 3 2 0 3

输出

1 2 3 6 7 9 5 4 8

输入

53 82 9 233 43 14 55 9 4 67 0 4

输出

4 9 9 14 43 233 55 82 53 67

输入

44 9 89 14 43 233 55 82 53 67 0 5

输出

9 14 43 44 53 233 55 82 89 67

堆排序：

在计算机科学中，堆（Heap）是一种基于树的数据结构，它具有以下特点：

  1. 完全二叉树结构： 堆通常被实现为一棵完全二叉树，这意味着除了最底层，其他层的节点都被填满，而且最底层的节点都集中在左侧。

  2. 堆序性质： 堆分为最大堆和最小堆。在最大堆中，每个节点的值都大于或等于其子节点的值；而在最小堆中，每个节点的值都小于或等于其子节点的值。

堆通常用于实现优先队列等抽象数据类型，其中最大（或最小）元素可以迅速地被查找和删除。

根据堆的性质，我们可以将堆分为两种主要类型：

  1. 最大堆（Max Heap）（大根堆）： 最大堆的每个节点的值都大于或等于其子节点的值。根节点包含堆中的最大元素。

  2. 最小堆（Min Heap）（小根堆）： 最小堆的每个节点的值都小于或等于其子节点的值。根节点包含堆中的最小元素。

堆排序通常使用数组来存储，但不限于数组，也可以用链表的方式进行存储，这里为方便起见使用数组进行演示。

这里首先要知道怎么用数组模拟完全二叉树：输出 key[1……n] 中 key[s] 的左节点为 key[2*s] ，右节点为 key[2*s+1]。且有 n 个节点的二叉树的深度 不会超过 log2(n)+1，非叶子节点的下标最大的节点下标为 n/2。

知道的这些就可进行推排序了：首先将所有的数据存入数组 key 中，从对的特点不难看出堆与二叉树的许多操作一样，具有递归性质，所以我们在对的排序过程中也会利用这一递归性质：搜先利用 HeapAdjust 函数对堆进行调整，使它成为大根堆或小根堆，这里以大根堆为例；先从非叶子节点的下标最大的节点 n/2 开始，对以 n/2 下标为根的二叉树进行堆排序，再对以 n/2-1，n/2-2……1 为根的二叉树进行堆排序。利用堆排序的递归性质，最大限度的提高算法的效率。

 HeapAdjust 函数：比较当前点与它左右孩子的大小，将它与他们三者中的最大值交换，继续以跟踪最大值，重复上述过程，知道不在变化为止。过程可以理解为大的值不断地往上浮，小的值不断往下沉。

时间复杂度O(nlog2(n)) 

6. (程序题)

试编写算法实现堆排序算法。

输出分两行：

第1行：输出初始堆，以行输出

第2行：输出排好序的数列

输入：
1 8 4 6 7 9 5 3 2 0
输出：

9 8 5 6 7 4 1 3 2 

1 2 3 4 5 6 7 8 9 

#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
using namespace std;
typedef long long LL;
const int N = 1e4;
typedef struct Heap {
	int key[N];
	int lenth;
}Heap;
void print(Heap& h) {
	for (int i = 1; i <= h.lenth; i++) {
		cout << h.key[i] << " ";
	}
	cout << endl;
}

void HeapAdjust(Heap&h,int u,int len) {
	/*cout << "KKKKKKKKKKKKKK   ";
	print(h);*/
	for (int j = 2 * u; j <=len; j *= 2) {
		if (j < len && h.key[j] < h.key[j + 1])j++;
		if (h.key[u] < h.key[j]) {
			//cout << "PPPPPPPPPPPPP  " << h.key[u] << " " << h.key[j] << endl;
			swap(h.key[u], h.key[j]);
			u = j;
			//cout << "PPPPPPPPPPPPP  " << h.key[u] << " " << h.key[j] << endl;
		}
		else {
			break;
		}
	}
	//cout << "KKKKKKKKKKKKKK   ";
	//print(h);
}



void HeapFun(Heap& h) {
	for (int i = h.lenth / 2; i > 0; i--) {
		//cout << "____________" << i << endl;
		HeapAdjust(h, i,h.lenth);
	}
	print(h);
	for (int i = h.lenth ; i > 1; i--) {
		swap(h.key[1], h.key[i]);
		HeapAdjust(h, 1,i-1);
	}
	print(h);
}

int main() {
	Heap h;
	h.lenth = 0;
	do {
		cin>>h.key[++h.lenth];
	} while (h.key[h.lenth]);
	h.lenth--;
	HeapFun(h);
	return 0;
}

用例1：

输入

1 8 4 6 7 9 5 3 2 0

输出

9 8 5 6 7 4 1 3 2 1 2 3 4 5 6 7 8 9

用例2：

输入

2 87 39 49 34 62 53 6 44 98 0

输出

98 87 62 49 34 39 53 6 44 2 2 6 34 39 44 49 53 62 87 98文章来源地址https://www.toymoban.com/news/detail-764327.html

到了这里，关于数据结构，第8章：排序(复习）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • 《数据结构与算法》之十大基础排序算法

    《数据结构与算法》之十大基础排序算法

    冒泡排序是一种交换排序，它的思路就是在待排序的数据中，两两比较相邻元素的大小，看是否满足大小顺序的要求，如果满足则不动，如果不满足则让它们互换。 然后继续与下一个相邻元素的比较，一直到一次遍历完成。一次遍历的过程就被成为一次冒泡，一次冒泡的结束

    2024年02月05日
    浏览(95)
  • 数据结构与算法基础（王卓）（28）：排序概述（分类）、直接插入排序思路

    数据结构与算法基础（王卓）（28）：排序概述（分类）、直接插入排序思路

    目录 排序分类：（本章目录） 按数据存储介质：（学习内容） 内部排序： 外部排序： 按比较器个数：（学习内容） 串行排序： 并行排序： 按主要操作：（学习内容、里面的排序都会重点学） 比较排序： 基数排序： 按辅助空间： 原地排序： 非原地排序： 按稳定性： 稳

    2023年04月26日
    浏览(39)
  • 【数据结构——9大基础排序】一文掌握九大经典排序（配有详细图文说明！！！）

    【数据结构——9大基础排序】一文掌握九大经典排序（配有详细图文说明！！！）

    算法基本思想：（从大到小排序） 在一个 非递减 的有序数组中，要新增一个元素 x ，有两个方法： 1.从数组的头部开始向后遍历，寻找 第一个比x 大 的元素 y ，从y元素开始的所有元素全部向后移动，最后将x元素插入数组。（×） 2.从数组的尾部开始向后向前遍历，寻找 第

    2024年02月08日
    浏览(42)
  • 算法、数据结构、计算机系统、数据库MYSQL、概率论、数学实验MATLAB、数学建模、马原、英语、杂项、QT项目

    算法、数据结构、计算机系统、数据库MYSQL、概率论、数学实验MATLAB、数学建模、马原、英语、杂项、QT项目

    可以三个条件 以此类推 （condition1）？x：（condition2）？y：z string变成int int 变成string 可以用循环 模运算展开式推导 我们要证明等式： (a * b) mod m = ((a mod m) * (b mod m)) mod m 假设 a = q1 * m + r1 ，其中 q1 是 a 除以 m 的商， r1 是 a 除以 m 的余数。类似地，假设 b = q2 * m + r2 ，其中

    2024年02月08日
    浏览(61)
  • 数据结构期末复习笔记

    数据结构期末复习笔记

    #搬运自己的原创笔记到这，从flowus# #因为后面时间不够了，所以没有把笔记做完，期末考试的最后的代码题一般都是书上的代码，考的简单，这个学期就是递归树。#       1.循环链表 2.双向链表 1.顺序栈 2.链栈 1.循环队列（顺序队列） 2.链式队列

    2024年01月21日
    浏览(44)
  • 数据结构（期末总复习）

    数据结构（期末总复习）

    目录 第一章 绪论 第二章 线性表 线性表常用操作辨析总结 第三章 栈和队列 第四章 串 第五章 数组与广义表 第六章 树 1.结构体成员的类型必须是基本数据类型。（F） 原因： 结构体成员类型不只是基本数据类型，同时也可以是另一种结构体类型，也可以是指针类型，同时也

    2024年02月03日
    浏览(46)

  • 数据结构复习

    什么是数据结构？数据结构是抽象数据类型的物理实现 抽象数据结构，怎么理解抽象 数据结构 抽象数据类型:对数据类型的描述，这种描述是抽象的，描述1.数据对象集，2.与数据集合关联的操作集 抽象:不依赖于具体实现，只描述是什么，不涉及如何做到 数据对象类型的抽

    2024年02月10日
    浏览(32)
  • 数据结构复习+答案

    数据结构复习+答案

    一、选择题：（每小题2分，共30分） 1、在数据的逻辑结构中，树结构和图结构都是（ ） A.非线性结构 B.线性结构 C.动态结构 D.静态结构 2.在一个长度为n的顺序表中插入一个元素的算法的时间复杂度为（ ） A.O（1） B.Ｏ（log n） C.O（n） D.O（n2） 3.指针p1和p2分别指向两个无头

    2024年02月12日
    浏览(42)
  • 【数据结构】复习题(一)

    【数据结构】复习题(一)

    一、选择题 1.组成数据的基本单位是()。 A. 数据项 B.数据类型 C.数据元素 D.数据变量 2.设数据结构A={D,R},其中D=｛1,2,3,4},R={r},r={1,2,2,3, 3,4,4,1}，则数据结构A是()。 A.线性结构 B.树型结构 C.图型结构 D.集合 3.数组的逻辑结构不同于下列()的逻辑结构。 A.线性表 B.栈 C.队列 D.树 4.二

    2024年02月04日
    浏览(43)
  • 数据结构期末复习（2）链表

    数据结构期末复习（2）链表

    链表（Linked List）是一种常见的数据结构，用于存储一系列具有相同类型的元素。链表由节点（Node）组成，每个节点包含两部分：数据域（存储元素值）和指针域（指向下一个节点）。通过节点之间的指针连接，形成一个链式结构。 链表可以分为单向链表和双向链表两种类型

    2024年02月03日
    浏览(52)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包