【问题引入】
在许多领域的研究与应用中,往往需要对反映事物的多个变量进行大量的观测,收集大量数据以便进行分析寻找规律。多变量大样本无疑会为研究和应用提供了丰富的信息,但也在一定程度上增加了数据采集的工作量,更重要的是在多数情况下,许多变量之间可能存在相关性,从而增加了问题分析的复杂性,同时对分析带来不便。如果分别对每个指标进行分析,分析往往是孤立的,而不是综合的。盲目减少指标会损失很多信息,容易产生错误的结论。因此需要找到一个合理的方法,在减少需要分析的指标同时,尽量减少原指标包含信息的损失,以达到对所收集数据进行全面分析的目的。由于各变量间存在一定的相关关系,因此有可能用较少的综合指标分别综合存在于各变量中的各类信息。主成分分析与因子分析就属于这类降维的方法。
【PCA原理】PCA即主成分分析,是用一个超平面对所有样本进行恰当表达的方法,思想是将n维特征映射到k维上(k<n),这k维是全新的正交特征。这k维特征称为主成分,是重新构造出来的k维特征,而不是简单地从n维特征中去除其余n-k维特征。由于它具有降维去噪的强大作用,通常在数据挖掘中起到很重要的作用。
【PCA算法步骤】
- 去平均值(即去中心化),即每一位特征减去各自的平均值。
-
计算协方差矩阵,
C = (X' * X) / (N-1)
注:这里除或不除样本数量N或N-1,其实对求出的特征向量没有影响。 - 求协方差矩阵的特征值与特征向量。
- 对特征值从大到小排序,选择其中最大的k个。然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P。
- 将数据转换到k个特征向量构建的新空间中,即Y=PX。
【性质】
- 缓解维度灾难:PCA 算法通过舍去一部分信息之后能使得样本的采样密度增大(因为维数降低了),这是缓解维度灾难的重要手段;
- 降噪:当数据受到噪声影响时,最小特征值对应的特征向量往往与噪声有关,将它们舍弃能在一定程度上起到降噪的效果;
- 过拟合:PCA 保留了主要信息,但这个主要信息只是针对训练集的,而且这个主要信息未必是重要信息。有可能舍弃了一些看似无用的信息,但是这些看似无用的信息恰好是重要信息,只是在训练集上没有很大的表现,所以 PCA 也可能加剧了过拟合;
- 特征独立:PCA 不仅将数据压缩到低维,它也使得降维之后的数据各特征相互独立;
【主程序代码】
%%
clear all;
close all;
% 生成一些样本数据
N = 100; % 样本数量
D = 2; % 数据维度
X = randn(N,D)*0.5 + repmat([2, 3], N, 1); % 生成高斯分布的数据
% 中心化数据
mu = mean(X);
X = X - repmat(mu, size(X,1), 1);
% 计算协方差矩阵
C = (X' * X) / (N-1);
% 计算特征向量和特征值
[V, D] = eig(C);
% 将特征向量按特征值从大到小排序
[~, I] = sort(diag(D), 'descend');
V = V(:,I);
% 选取前k个特征向量
k = 1;
W = V(:,1:k);
% 将数据投影到新的空间中
Y = X*W;
% 可视化结果
figure;
scatter(X(:,1), X(:,2), 'filled', 'MarkerFaceColor', 'b');
hold on;
quiver(mu(1), mu(2), W(1), W(2), 'r', 'LineWidth', 2);
xlabel('X1');
ylabel('X2');
title('Principal Component Analysis (PCA)');
【程序分析】
- 生成样本数据:通过使用 randn 函数生成 N 个二维高斯分布的样本数据,然后加上一个偏置项 [2, 3],并存储在名为 X 的矩阵中。
- 中心化数据:计算数据的均值 mu,然后使用 repmat 函数将其复制成与 X 大小相同的矩阵,并将其从 X 中减去,实现数据的中心化。
- 计算协方差矩阵:使用公式 C = (X’ * X) / (N-1) 计算数据的协方差矩阵 C,其中 X’ 表示 X 的转置。
- 计算特征向量和特征值:使用 eig 函数计算协方差矩阵 C 的特征向量 V 和特征值 D。
- 特征向量排序:使用 sort 函数和 diag 函数将特征向量 V 按照特征值 D 的从大到小的顺序进行排序,并存储在 V 中。
- 选择主成分:在这个例子中,我们选择第一个主成分,即特征值最大的特征向量,将其存储在名为 W 的矩阵中。
- 将数据投影到新的空间中:将中心化的数据 X 与选定的主成分 W 相乘,得到投影后的数据 Y。
- 可视化结果:使用 scatter 函数绘制原始数据的散点图,并使用 quiver 函数绘制原始数据的均值 mu 和选定的主成分 W 的方向。
这个程序演示了如何使用主成分分析(PCA)对二维数据进行降维,并将数据投影到新的一维空间中。
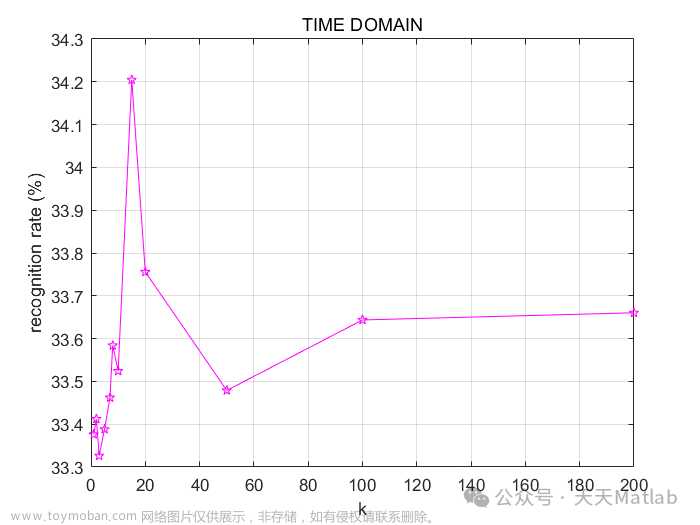
【运行结果】
 文章来源:https://www.toymoban.com/news/detail-764363.html
文章来源:https://www.toymoban.com/news/detail-764363.html
喜欢我就关注我吧!!!! 文章来源地址https://www.toymoban.com/news/detail-764363.html
文章来源地址https://www.toymoban.com/news/detail-764363.html
到了这里,关于【机器学习】主成分分析(PCA)算法及Matlab实现的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!