微信公众号上线,搜索公众号***小灰灰的FPGA***,关注可获取相关源码,定期更新有关FPGA的项目以及开源项目源码,包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等
线性分组码之监督矩阵、生成矩阵、编解码计算
以(n,k)码为例,进行码长n,信息位k,最小码距d0,纠错能力t,校正子计算
(1)监督矩阵H
监督矩阵H是一个r×n阶(r行n列)矩阵,r为监督位长,n为码长
典型监督矩阵,具有[PIr]形式的H矩阵
P为r×k阶矩阵;Ir为r×r阶矩阵
(2)生成矩阵G
生成矩阵G是一个k×n阶(k行n列)矩阵,k为信息位长,n为码长
典型生成矩阵,具有[IkQ]形式的G矩阵
Ik为k×k阶矩阵;Q为k×r阶矩阵,是P的转置矩阵
由典型生成矩阵G得出的码组A中,信息位的位置不变,监督位附加于其后,这种形式的码称为系统码
(3)校正子与译码
线性分组码的编码码组A满足:
线性分组码的译码码组B满足:
若校正子S=0,表示接收码组B无错;
若校正子S≠0
E为错误图样,译码或者纠错后的码组A=B+E
S称为接收码组B的校正子
例题一:
已知某线性分组码的生成矩阵G如下,并求:
①码长n,信息位长k,最小码距d0,纠错能力;
②若信息码为1011,求编码结果。该码是否是系统码?若不是,求系统码编码结果;
③校验矩阵H(典型阵);
④若接收码字是1100011,求校正子。该码是否是正确码?若是错码,请纠正。
解析:
①生成矩阵G是一个k×n阶(k行n列)矩阵,k为信息位长,n为码长
则码长为7,信息位长为4
典型生成矩阵G(典型)的求解
G的第2行与第3行异或可得:0001011
G的第2行与第4行异或可得:0010101
G的第1行与0001011异或可得:1000111
G的第4行与0001011异或可得:0100110
故G(典型)
有A=[a6a5a4a3]·G;
则所有码组为:
a6a5a4a3a2a1a0
0000000
0001011
0010101
0011110
0100110
0101101
0110011
0111000
1000111
1001100
1010010
1011001
1100001
1101010
1110100
1111111
编码为1的个数最小为3,故最小码距d0为3
根据d0≥2t+1,则t=1
②信息码1011,对应的系统码为1011001
③由G=[IkQ]可得Q
P为Q的转置矩阵,则
H=[PIr]
④接收码组为1100011
S=010,为错码
由所有码组可得,由于只能纠错一位,故接收端的码字应为1100001
例题二:
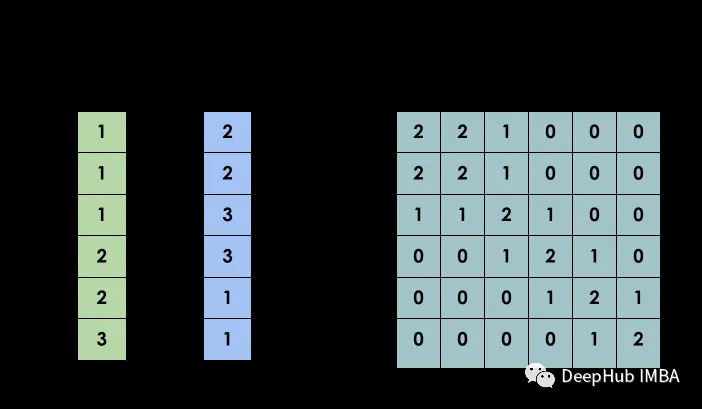
已知某线性分组码的校验矩阵H如下,求:
①码长n,信息位长k;
②典型生成矩阵G,若信息码为1010,求编码;
③最小码距d0,纠错能力t;
④若接收码字是1010101,求校正子,并判断是否是正确码字。
解析:
①监督矩阵H是一个r×n阶(r行n列)矩阵,r为监督位,n为码长
故码长n=7,信息位长k=n-r=3
②典型监督矩阵H(监督)
将H的第一行与第三行异或可得:1000111
将H的第一行与1000111异或可得:1110100
将H的第三行0011110与1110100异或可得:1101010
故H(监督)
由H=[PIr]可得P
由G=[IkQ]可得Q
Q为P的转置矩阵,则
G=[IkQ]
有A=[a6a5a4a3]·G;
则信息码为1010,对应的系统码编码为1010010
③根据A=[a6a5a4a3]·G
则所有码组为:
a6a5a4a3a2a1a0
0000000
0001011
0010101
0011110
0100110
0101101
0110011
0111000
1000111
1001100
1010010
1011001
1100001
1101010
1110100
1111111
编码为1的个数最小为3,故最小码距d0为3
根据d0≥2t+1,则t=1
④接收码组为1010101
S=111,为错码
由所有码组可得,由于只能纠错一位,故接收端的码字应为0010101文章来源地址https://www.toymoban.com/news/detail-764548.html
文章来源:https://www.toymoban.com/news/detail-764548.html
到了这里,关于通信原理板块——线性分组码之监督矩阵、生成矩阵、编解码计算的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!