C++深度优先搜索(DFS)算法的应用：树中可以形成回文的路径数-Toy模板网

这篇具有很好参考价值的文章主要介绍了C++深度优先搜索(DFS)算法的应用：树中可以形成回文的路径数。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

本文涉及知识点

深度优先搜索(DFS) 状态压缩

题目

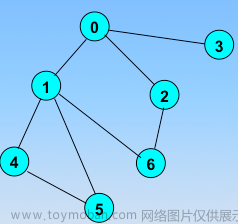
给你一棵树（即，一个连通、无向且无环的图），根节点为 0 ，由编号从 0 到 n - 1 的 n 个节点组成。这棵树用一个长度为 n 、下标从 0 开始的数组 parent 表示，其中 parent[i] 为节点 i 的父节点，由于节点 0 为根节点，所以 parent[0] == -1 。
另给你一个长度为 n 的字符串 s ，其中 s[i] 是分配给 i 和 parent[i] 之间的边的字符。s[0] 可以忽略。
找出满足 u < v ，且从 u 到 v 的路径上分配的字符可以重新排列形成回文的所有节点对 (u, v) ，并返回节点对的数目。
如果一个字符串正着读和反着读都相同，那么这个字符串就是一个回文。
示例 1：
输入：parent = [-1,0,0,1,1,2], s = “acaabc”
输出：8
解释：符合题目要求的节点对分别是：

(0,1)、(0,2)、(1,3)、(1,4) 和 (2,5) ，路径上只有一个字符，满足回文定义。
(2,3)，路径上字符形成的字符串是 “aca” ，满足回文定义。
(1,5)，路径上字符形成的字符串是 “cac” ，满足回文定义。
(3,5)，路径上字符形成的字符串是 “acac” ，可以重排形成回文 “acca” 。
示例 2：
输入：parent = [-1,0,0,0,0], s = “aaaaa”
输出：10
解释：任何满足 u < v 的节点对 (u,v) 都符合题目要求。
参数提示
n == parent.length == s.length
1 <= n <= 105
对于所有 i >= 1 ，0 <= parent[i] <= n - 1 均成立
parent[0] == -1
parent 表示一棵有效的树
s 仅由小写英文字母组成

解法一稍稍超时，通过不了

分析

状态压缩

排序后能构成回文，那只有两种可能，一：所有字符数量都为偶数。二，有一个字符数量为奇数，其余全部是偶数。可以用二进制状态压缩，每个二进制位表示某个字符是否为偶数。1表示z是奇数数量,2表示y是奇数数量,3表示yz都是奇数数量。

异或（^)

增加一个字符可以用异或操作，由于异或的逆操作就是自己，所以删除字符也用异或。

难理解的地方

mNums记录以下路径：


一	起点和终点都是cur的路径
二	起点是cur，终点是已处理子树的任意节点

childNums：记录以child为起点，以child为根节点的子树的任意节点为终点的路径。

下面以{-1,0,0}来说明，由于起点是固定的，所以下表只记录终点。路径指的是：以child子树中的节点为起点，以mNums中的节点为终点的路径

	mNums	childNums	路径
处理根节点	{0}	{}
处理节点1	{0}	{1}	{0,1}
处理节点2	{0,1}	{2}	{0,2},{1,2}
	{0,1,2}

总结：第四列的路径，就是mNums 和childNums 各取一个节点的两两组合。

注意：
一个节点没有字符，所以不是合法路径。

ChangeNum

不要枚举mNums 和childNums ，枚举其中的一个和27种合法可能。

核心代码

class Solution {
public:
long long countPalindromePaths(vector& parent, string s) {
m_c = parent.size();
m_str = s;
m_vNeiBo.assign(m_c, vector());
for (int i = 0; i < 26; i++)
{
m_iVilidMask[i] = 1 << i;
}
m_llRet = 0;
int iRoot = -1;
for (int i = 0; i < m_c; i++)
{
if (-1 == parent[i])
{
iRoot = i;
}
else
{
m_vNeiBo[parent[i]].emplace_back(i);
}
}
std::unordered_map<int, int> mNums;
dfs(iRoot, mNums);
return m_llRet ;
}
void dfs(int cur, std::unordered_map<int, int>& mNums)
{
const int curMask = 1 << (m_str[cur] - ‘a’);
mNums[curMask]++;
for (const auto& child : m_vNeiBo[cur])
{
std::unordered_map<int, int> childNums;
dfs(child, childNums);
ChangeNum(mNums, childNums,curMask);
for (const auto& it : childNums)
{
mNums[it.first ^ curMask] += it.second;
}
}
}
void ChangeNum(const std::unordered_map<int, int>& mNums, const std::unordered_map<int, int>& childNums, const int curMask )
{
for (const auto& it : childNums)
{
for (int i = 0; i < 27; i++)
{
const int iNeedMask = it.first ^ m_iVilidMask[i] ^ curMask;
if (mNums.count(iNeedMask))
{
m_llRet += (long long)it.second * mNums.find(iNeedMask)->second;
}
}
}
}
//状态压缩 1表示z是奇数数量,2表示y是奇数数量,3表示yz都是奇数数量
int m_iVilidMask[27] = { 0 };//记录所有字符都是偶数和只有一个字符是奇数
vector<vector> m_vNeiBo;
//vector m_vNums;
int m_c;
long long m_llRet = 0;//不包括单节点的合法路径数
string m_str;
};

测试用例

template
void Assert(const vector& v1, const vector& v2)
{
if (v1.size() != v2.size())
{
assert(false);
return;
}
for (int i = 0; i < v1.size(); i++)
{
Assert(v1[i], v2[i]);
}
}

int main()
{
Solution slu;
vector parent;
long long res;
string s;
parent = { -1 };
s = “a”;
res = slu.countPalindromePaths(parent, s);
Assert(res, 0LL);
parent = { -1,0 };
s = “aa”;
res = slu.countPalindromePaths(parent, s);
Assert(res, 1LL);
parent = { -1,0,1 };
s = “aaa”;
res = slu.countPalindromePaths(parent, s);
Assert(res, 3LL);
parent = { -1,0,0 };
s = “aaa”;
res = slu.countPalindromePaths(parent, s);
Assert(res, 3LL);
parent = { -1,0,0 };
s = “aba”;
res = slu.countPalindromePaths(parent, s);
Assert(res,2LL);
parent = { -1,0,0 };
s = “baa”;
res = slu.countPalindromePaths(parent, s);
Assert(res, 3LL);
parent = { -1,0,0,1,1,2 };
s = “acaabc”;
res = slu.countPalindromePaths(parent, s);
Assert(res, 8LL);
parent = { -1, 0, 0, 0, 0 };
s = “aaaaa”;
res = slu.countPalindromePaths(parent, s);
Assert(res, 10LL);

//CConsole::Out(res);

}

解法二

分析

假定节点A,B的公共最近祖先是C，那么A到B的路径为:A->C->B和路径A->0->B的字符数量的奇偶性相同。A->0可以拆分成A->C->0 ，0->B可以拆分成0->C->B。0到C和C到0抵消了。
###　时间复杂度
o(27n)。n是节点数量,27是合法掩码的数量。

代码

class Solution{
public:
	long long countPalindromePaths(vector<int>&parent, string s) {
		m_c = parent.size();
		m_str = s;
		m_vNeiBo.assign(m_c, vector<int>());
		for (int i = 0; i < 26; i++)
		{
			m_iVilidMask[i] = 1 << i;
		}
		m_llRet = 0;
		m_mMaskNums.clear();
		int iRoot = -1;
		for (int i = 0; i < m_c; i++)
		{
			if (-1 == parent[i])
			{
				iRoot = i;
			}
			else
			{
				m_vNeiBo[parent[i]].emplace_back(i);
			}
		}
	
		dfs(iRoot,0);
		return m_llRet;
	}
	void dfs(int cur,int iMask)
	{
		const int curMask = iMask ^ ( 1 << (m_str[cur] - 'a'));
		for (int i = 0; i < 27; i++)
		{
			const int iNeedMask = m_iVilidMask[i] ^ curMask;
			if (m_mMaskNums.count(iNeedMask))
			{
				m_llRet += m_mMaskNums[iNeedMask];
			}
		}
		m_mMaskNums[curMask]++;
		for (const auto& child : m_vNeiBo[cur])
		{
			dfs(child, curMask);
		}
	}
	int m_iVilidMask[27] = { 0 };//记录所有字符都是偶数和只有一个字符是奇数
	vector<vector<int>> m_vNeiBo;
	std::unordered_map<int,int> m_mMaskNums;
	int m_c;
	long long m_llRet = 0;//不包括单节点的合法路径数
	string m_str;
};

扩展阅读

视频课程

有效学习：明确的目标及时的反馈拉伸区（难度合适），可以先学简单的课程，请移步CSDN学院，听白银讲师（也就是鄙人）的讲解。
https://edu.csdn.net/course/detail/38771

如何你想快速形成战斗了，为老板分忧，请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176

鄙人想对大家说的话
闻缺陷则喜是一个美好的愿望，早发现问题，早修改问题，给老板节约钱。
墨家名称的来源：有所得以墨记之。
如果程序是一条龙，那算法就是他的是睛