最小生成树——普利姆（Prim）算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了最小生成树——普利姆（Prim）算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

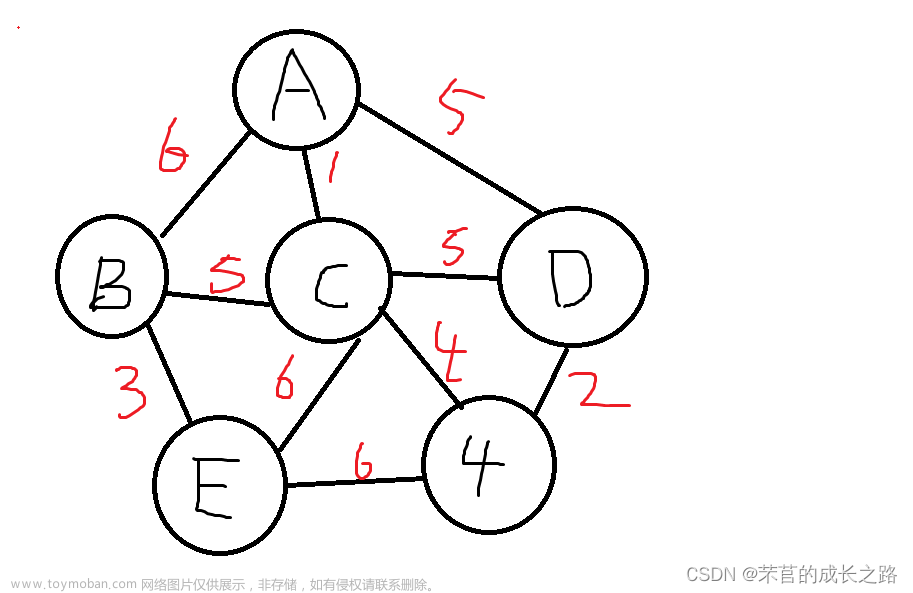
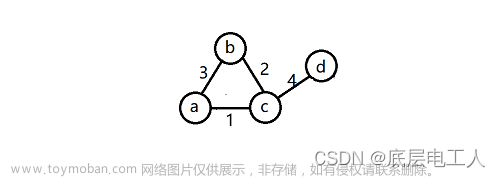
构成连通网的最小代价生成树称为最小生成树（Minimun Cost Spanning Tree).

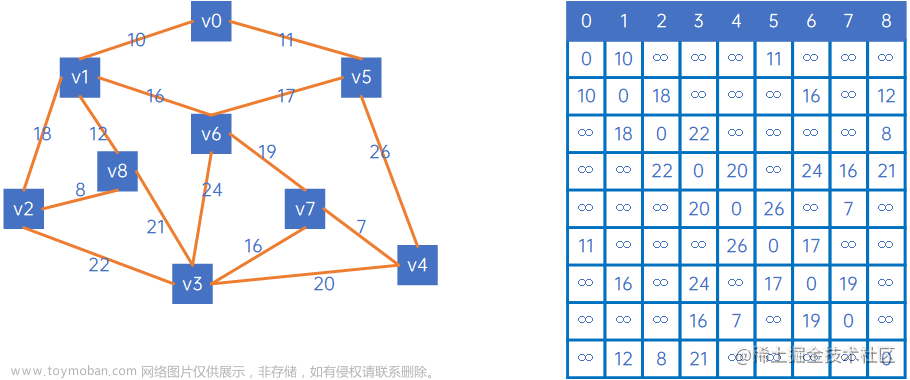
最小生成树可以运用到生活中，假如你是一位工程师，需要为一个镇的九个村庄架设通信网络做设计，村庄位置大值如下图：

6-3 最小生成树(普里姆算法,总结,算法,图论,数据结构

其中 V0~V8 是村庄，之间连线的数字表示村与村间的可通达的直线距离，比如 V0 至 V1 就是 10 千米（个别如 V0 与 V6，V6 与 V8，V5 与 V7 为测算距离是因为有高山或者湖泊，不予考虑）。你们领导要求你必须用最小的成本完成本次任务。该怎么做？

样例输入

9 15
0 1 10
0 5 11
1 6 16
6 5 17
1 2 18
1 8 12
2 8 8
2 3 22
3 8 21
3 6 24
6 7 19
3 7 16
3 4 20
4 5 26
4 7 7

样例输出

(0,1)
(1,8)
(1,6)
(6,7)
(7,4)
(8,2)
(7,3)
(0,5)

这是一个带权值的图，即网状结构。要求最小成本，就是 n 个顶点，用 n-1 条边连接起来，并且使得权值的和最小。

一个连通图的生成树是一个极小的连通子图，它包含图中所有的顶点，足以构成树的 n-1 条边，而构成连通网的最小代价生成树被称为最小生成树。

普利姆算法（Prim）

输入的信息可以用邻接矩阵来存储，样例输入的信息转化为邻接矩阵如下：

6-3 最小生成树(普里姆算法,总结,算法,图论,数据结构

解题思路：

在转化成邻接举证时，要注意初始化，先把数字都赋为一个较大值（99999999），然后再输入数字，输入一个就修改两处，例如输入 x，y，z，那么要把二维矩阵的 a[x][y] = z，a[y][x] = z，因为该图是双向的。

在当前可选路中选出最短的那条路。我们的目的是在不成环的前提下，连通所有结点，而不是一步遍历所有结点，所以当我们获取下一条路径时，我们的出发点可以是已走路径上的任意一点。

先选择一个起点，我们从V0 开始（不一定是 V0，也可以是其他村庄编号）。

从 V0 村庄到各个村庄的路程（包括 V0 村庄不可直接到达的村庄）记录进 lowcost 数组，然后找到数组中的最小值，记录下最小值的下标，并输出两个村庄的编号，连通好的村庄不要重复连通，此时可以将 lowcost 数组对应的下标赋为 0，当 lowcost 数组为 0 时，跳过该点要进行的操作。

利用 adjvex 数组记录当前 lowcost 数组存放的最小值是哪个村庄的编号。

代码如下：文章来源地址https://www.toymoban.com/news/detail-765052.html

#include<stdio.h>
int a[1000][1000];//二维邻接矩阵 
int num,n;//num表示一共有多少顶点间的边，n表示顶点个数 
void MinSpanTree_Prim()
{
	int min,i,j,k;
	int adjvex[1000];//存储顶点间边的权值下标 
	int lowcost[1000];//存储当前权值（如果值为 0，说明已经经过该点） 
	adjvex[0]=0;//V0的权值为 0，表示以 V0为起点，V0加入生成树 
	lowcost[0]=0;//初始化第一个顶点的下标为 0 
	//将邻接矩阵中 V0的那行赋值给 lowcost数组 
	for(i=1;i<n;i++)
	{
		lowcost[i]=a[0][i];
		adjvex[i]=0;//初始化都为 V0的下标 
	}
	for(i=1;i<n;i++)
	{
		min=99999999;//将 min赋值为一个较大的数 
		j=1;//从 V1村庄开始找最小路径 
		k=0;//当前顶点到以 k为下标村庄的最小路径 
		for(j=1;j<=n;j++)//循环所有的点 
		{
			if(lowcost[j]!=0&&lowcost[j]<min)//首先该点未加入生成树（lowcost[j]!=0），而且要替换的话，要小于当前的 min 
			{
				min=lowcost[i];//更换最小值 min 
				k=j;//将当前最小值的下标存入 k 
			}
		}
		printf("(%d,%d)\n",adjvex[k],k);//找到后输出 
		lowcost[k]=0;//两村庄连通后，将它的下标所在的 lowcost数组赋为 0，表示已加入生成树 
		for(j=1;j<n;j++)//以村庄 V1开始，如果村庄未连通且邻接矩阵中对应的值小于临时数组 lowcost，就替换 
		{
			if(lowcost[j]!=0&&a[k][j]<lowcost[j])
			{
				lowcost[j]=a[k][j];
				adjvex[j]=k;//将下标为 k的村庄存入 adjvex数组 
			}
		}
	}
}
int main()
{
	int i,j;
	int x,y,z;
	scanf("%d %d",&n,&num);
	//这步初始化不能忘记，否则肯定出错 
	for(i=0;i<num;i++)
	{
		for(j=0;j<num;j++)
		{
			a[i][j]=99999999;//将二维矩阵的值赋成一个较大值，表示两顶点之间难以通过 
		}
	}
	//依次输入信息 
	for(i=0;i<num;i++)
	{
		scanf("%d %d %d",&x,&y,&z); 
		a[x][y]=z;//这里是双向图，两边可以相互到达 
		a[y][x]=z;
	}
	MinSpanTree_Prim();//Prim算法生成最小生成树 
	return 0;
}

到了这里，关于最小生成树——普利姆（Prim）算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！