实验12 图论基础-Toy模板网

这篇具有很好参考价值的文章主要介绍了实验12 图论基础。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

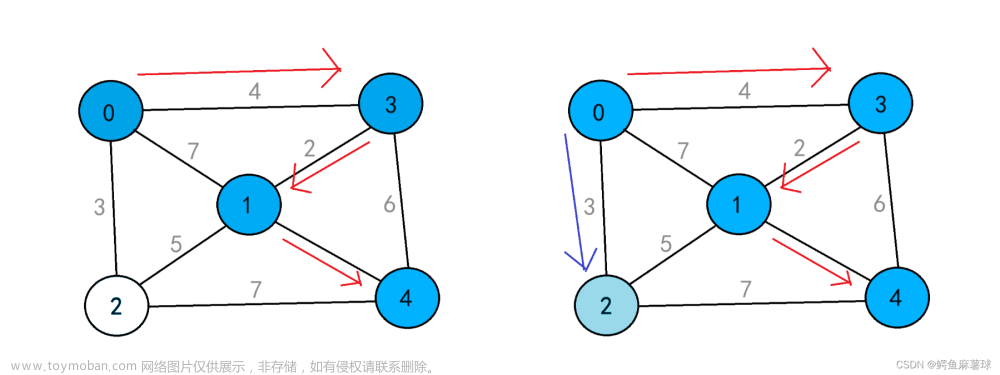
描述

创建无向图类，存储结构使用邻接链表，提供操作：插入一条边，删除一条边，BFS，DFS。

格式

输入

第一行四个整数n，m，s，t。n ( $\leq n \leq 100000$ ) 代表图中点的个数，m ( $\leq m \leq 200000$ ) 代表接下来共有m个操作，s代表起始点，t代表终点。
接下来m行，每行代表一次插入或删除边的操作，操作格式为：

0 u v 在点u和v之间增加一条边
1 u v 删除点u和v之间的边

输出

第一行输出图中有多少个连通分量

第二行输出所有连通子图中最小点的编号（升序），编号间用空格分隔

第三行输出从s点开始的dfs序列长度

第四行输出从s点开始的字典序最小的dfs序列

第五行输出从t点开始的bfs序列的长度

第六行输出从t点开始字典序最小的bfs序列

第七行输出从s点到t点的最短路径，若是不存在路径则输出-1

思路和探讨

图相关知识

笔记补充——第十六章：图

整体思路描述

辅助工具，链队列模板的应用。
图论基础相关操作实现首先需要完成图论基础的相关定义，而后依次定义并实现插入边、删除边、深度优先算法、广度优先算法、计算序列长度、计算连通分量、输出连通子图中的最小点的编号、计算最短路径相关功能。

细节思路补充

1.图类定义

template<class T>
class graph//图类
{
	public:
		graph(int n=100)//构造函数
		{
			G.Vnumber=n;//图G有n个节点
			for(int i=0;i<n;i++)
			{
				G.Vlist[i].element=i+1;//存放节点1~n
				G.Vlist[i].firstNode=NULL;//节点后方连NULL
			}
		}
		void insert(int u,int v);//插入边(u,v)
		void erase(int u,int v);//删除边(u,v)
		void bfs(int n);//bfs算法
		void dfs(int n);//dfs算法
		void dfsCounter(int n);//计算序列长度 
		void fdfs(int n);//辅助求得连通分量 
		void components(int n);//图中连通分量的个数
		void everyComponents(int n);//图中连通分量最小点的编号
		void path(int s,int t);//从s点到t点的最短路径
	protected:
		ALGraph G;//图G		
};

按题意是要构建无向图类，这里构建的是加权有向图，而

无权有向图和无向图可以看作每条边的权值是1的加权有向图和无向图

无向图，边(i,j)存在可以看作边(i,j)和边(j,i)都存在的有向图

2.边的插入删除

若在存顶点时是从0开始的，那在操作时要找的对应位置是u = u-1和v = v-1

这里因为是无向图，边(u,v)存在可以看作边(u,v)和边(v,u)都存在的有向图，所以插入删除都要完成双向

在插入和删除过程中，是升序查找对应的顶点，所以最后插入/删除后整个链表也是按存的顶点值升序排列。

insert(int u,int v)插入边(u,v)
①链表G.Vlist[u]中插入元素v
②链表G.Vlist[v]中插入元素u
③G.Anumber++，图的边数+1
插入思路（以链表G.Vlist[u]中插入元素v）为例：
- 情况①：u没有指向的边或者它指的第一条边对应的顶点是比v大的
  - 直接构建表头u先指向v
- 情况②：u有指向的边且它指的第一条边对应的顶点是比v小的
  - 往后寻找插入位置
  - 在找到的插入位置插入
    - 若到底了，v就是最大顶点，就插在最后方
erase(int u,int v)删除边(u,v)
① 若(u,v)存在，链表G.Vlist[u]中删除元素v
②若(v,u)存在，链表G.Vlist[v]中删除元素u
③ G.Anumber--，图的边数-1
删除思路（以链表G.Vlist[u]中删除元素v）为例
- 先搜索v
  - 若没找到，输出none
  - 若找到v
    - v是所指向的第一个顶点
      
      G.Vlist[u].firstNode = current->next;
    - v不是所指向的第一个顶点（v的前一个指向v的下一个）
      
      trail->next = current->next;

3.深度优先搜索`(DFS)`

创建无向图类,存储结构使用邻接链表,提供操作:插入一条边,删除一条边,bfs,dfs。,# 数据结构实验合集,数据结构、算法与应用,图论,深度优先,算法

要设置一个类型为bool变量的辅助数组vertex，来标记顶点是否被访问过。

深度优先遍历主要思路是从图中一个未访问的顶点 V 开始，沿着一条路一直走到底，然后从这条路尽头的节点回退到上一个节点，再从另一条路开始走到底…，不断递归重复此过程，直到所有的顶点都遍历完成，它的特点是不撞南墙不回头，先走完一条路，再换一条路继续走。

输出dfs序列实现伪码

template<class T>
void graph<T>::dfs(int n)
{
    输出起点顶点n;
    将n标记为已到达顶点;
	for(每一个与n邻接的尚未到达的顶点u)
    {
        后边还有要输出的元素，输出空格;
        dfs(u);
    }
}

4.广度优先遍历`(BFS)`

创建无向图类,存储结构使用邻接链表,提供操作:插入一条边,删除一条边,bfs,dfs。,# 数据结构实验合集,数据结构、算法与应用,图论,深度优先,算法

如果说深度优先遍历是一次遍历一个，那么广度优先遍历就是一次遍历一层,故这里要运用到队列这种先进先出的输出方法，算法思想为：

访问出发点v，并将其标记为已访问过

顶点v入队

当队列不为空时

取出队首顶点i

依次搜索顶点i的所有邻接点，若某一邻接点 j未被访问，则访问该邻接点，并将其入队

输出bfs序列实现伪码

template<class T>
void graph<T>::dfs(int n)
{
	初始化队列Q;
    将起点顶点push进队列Q;
    while(Q不空)
	{
        输出队列首w的顶点(记得加空格);
        标记该顶点w;
        令u为邻接于w的顶点;
        while (u!=NULL)
		{
            if(u尚未被标记)
            {
                把u加入队列;
				把u标记为已到达顶点;
            }
            u = 邻接于w的下一个顶点;
        }
        把顶点w从队列中pop掉;
    } 
}

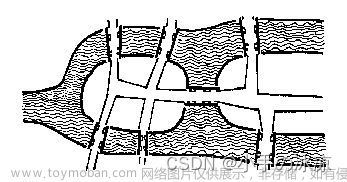
5.连通分量计算

连通分量就看有几个不间断的部分，例：
实现思路：

遍历所有顶点，标记这个顶点所能到的所有顶点

有中断，连通分量＋1，继续遍历和标记

6.连通子图中最小点的编号

基于连通分量计算，找到每个子图的最小顶点并输出

7.最短路径计算

创建无向图类,存储结构使用邻接链表,提供操作:插入一条边,删除一条边,bfs,dfs。,# 数据结构实验合集,数据结构、算法与应用,图论,深度优先,算法

bfs算法我们可以看作是以起点开始，一层一层往外访问，规定起点是第0层，即第0层的距离为0，第N层的顶点距起点的距离为N。

第0层：访问A，A到起点的距离为0。

第1层：访问第0层顶点（A）的邻接点，且这些邻接点之前没有被访问过，即访问C、E ，C 、E到起点的距离为1。

第2层：访问第1层顶点（C、E）的邻接点，且这些邻接点之前没有被访问过，即访问D、B，D、B到起点的距离为2。注意A也是C、E的邻接点但之前已经访问过，所以本层不再访问。

第3层：访问第二层的邻接节点中之前没有被访问的节点：B距离为3。

若已看懂思路，试着自己写~

特别提醒：不同功能实现后，顶点标记记得重置~文章来源地址https://www.toymoban.com/news/detail-765189.html

实现代码

#include<iostream>
using namespace std;

//--------------链队列模板应用start--------------
template <class T>//链表节点的结构定义
struct chainNode 
{
	//数据成员 
   T element; 
   chainNode<T> *next;
   //方法 
   chainNode() {}
   chainNode(const T& element)
      {this->element = element;}
   chainNode(const T& element, chainNode<T>* next)
      {this->element = element;
       this->next = next;}
};

template<class T>
class linkedQueue //链队列定义
{
   public:
    	linkedQueue(int initialCapacity = 10)//初始化 
        {
        	queueFront = NULL; queueSize = 0;
		}
    	~linkedQueue();//析构函数 
    	bool empty()const{return ((queueFront)?false:true);};
    	T& front()//返回头元素的引用 
        {
            if (queueSize == 0)
            	exit(1);
            return queueFront->element;
        }
    	T& back()//返回尾元素的引用 
        {
            if (queueSize == 0)
            	exit(1);
            return queueBack->element;
        }
     	void pop();//删除首元素 
      	void push(const T& theElement);//把元素theElement加入队尾 
   private:
    	chainNode<T>* queueFront;//头结点  
    	chainNode<T>* queueBack;//尾结点 
    	int queueSize;//队列元素的个数      
};

template<class T>
linkedQueue<T>::~linkedQueue()
{//析构函数 
   while (queueFront != NULL)
   {
      chainNode<T>* nextNode = queueFront->next;
      delete queueFront;
      queueFront = nextNode;
   }
}

template<class T>
void linkedQueue<T>::pop()
{//删除首元素
    if (queueFront == NULL)
    	exit(1);
	chainNode<T>* nextNode = queueFront->next;
   	delete queueFront;
   	queueFront = nextNode;
   	queueSize--;
}

template<class T>
void linkedQueue<T>::push(const T& theElement)
{//把元素theElement加入队尾
   	chainNode<T>* newNode = new chainNode<T>(theElement, NULL);
   	if (queueSize == 0)
      	queueFront = newNode;      
   	else 
      	queueBack->next = newNode;  
   	queueBack = newNode;
	queueSize++;
}
//---------------链队列模板应用finish---------------

//------------------图论基础start------------------
bool vertex[100000];//顶点标记数组
int f = 0;//用来记录序列长度

struct EdgeNode//边结点类
{
	int vertexAround;//该边指向的顶点的位置
	struct EdgeNode*next;//指向下一条边的的指针
	int weight;//该边权值
};


struct ADVList//表头结点
{
	EdgeNode*firstNode;//指向第一条依附于该表头的指针
	int element;//存放定点信息
};


struct ALGraph//邻接表
{
	ADVList Vlist[100000];//创建一个有100000个结点的图
	int Vnumber,Anumber;//图的定点数和边数
};

template<class T>
class graph//图类
{
	public:
		graph(int n=100)//构造函数
		{
			G.Vnumber=n;//图G有n个节点
			for(int i=0;i<n;i++)
			{
				G.Vlist[i].element=i+1;//存放节点1~n
				G.Vlist[i].firstNode=NULL;//节点后方连NULL
			}
		}
		void insert(int u,int v);//插入边(u,v)
		void erase(int u,int v);//删除边(u,v)
		void bfs(int n);//bfs算法
		void dfs(int n);//dfs算法
		void dfsCounter(int n);//计算序列长度 
		void fdfs(int n);//辅助求得连通分量 
		void components(int n);//图中连通分量的个数
		void everyComponents(int n);//图中连通分量最小点的编号
		void path(int s,int t);//从s点到t点的最短路径
	protected:
		ALGraph G;//图G
		
};

template<class T>
void graph<T>::insert(int u,int v)
{//插入边(u,v) 
	u = u-1;
	v = v-1;
	EdgeNode*p1 = new EdgeNode;
	p1->vertexAround = v;//p1指向v
	EdgeNode*p = G.Vlist[u].firstNode;
	EdgeNode*pp = NULL;//用来记录p的前一个顶点，随p后移
	if(p == NULL||p->vertexAround > v)
	{//u没有指向的边或者它指的第一条边对应的顶点是比v大的
		p1->next = G.Vlist[u].firstNode;
		G.Vlist[u].firstNode = p1;//直接构建表头u先指向v
	}
	else
	{
		while(p && p->vertexAround < v)
		{//寻找插入位置，p不为空且p的下一个顶点比v小
			pp = p;
			p = p->next;
		}
		if(!p)
		{//p为空了，到底了，v就是最大顶点，插入在最后方
			pp->next = p1;
			p1->next = NULL;
		}
		else
		{//在所有顶点中的某个位置找到合适插入点
			p1->next = pp->next;
			pp->next = p1;
		}
	}
	
	//另一个方向 
	EdgeNode*q2 = new EdgeNode;
	q2->vertexAround = u;
	EdgeNode*q = G.Vlist[v].firstNode;
	EdgeNode*qq = NULL;
	if(q == NULL||q->vertexAround > u)
	{
		q2->next = G.Vlist[v].firstNode;
		G.Vlist[v].firstNode = q2;
	}
	else
	{
		while(q && q->vertexAround < u)
		{
			qq = q;
			q = q->next;
		}
		if(!q)
		{
			qq->next = q2;
			q2->next = NULL;
		}
		else
		{
			q2->next = qq->next;
			qq->next = q2;
		}
	}
	G.Anumber++;//图的边数+1
	
}

template<class T>
void graph<T>::erase(int u,int v)
{//删除边(u,v)
	u = u-1;
	v = v-1;
	//删除边(u,v)
    //用current定位顶点u(链表表头)
	EdgeNode*current = G.Vlist[u].firstNode;
    //用来记录current的前一个顶点，随current后移
	EdgeNode*trail = NULL;
    //搜索v
	while(current != NULL && current->vertexAround != v)
	{//u有指向的顶点并且u指向的节点不是v
		trail = current;//后移
		current = current->next;
	}
	if(current == NULL)
	{//到底了没找到v，说明没有这条边
		cout<<"none"<<endl;
		return;
	}
	if(trail != NULL)
	{//v不是所指向的第一个顶点
		trail->next = current->next;
	}
	else
	{//v是所指向的第一个顶点
		G.Vlist[u].firstNode = current->next;
	}
	delete current;//删掉current节点
	
	//另一个方向，删除边(v,u)
	EdgeNode*current2 = G.Vlist[v].firstNode;
	EdgeNode*trail2 = NULL;
	while(current2 != NULL && current2->vertexAround != u)
	{
		trail2 = current2;
		current2 = current2->next;
	}
	if(current2 == NULL)
	{
		cout<<"none"<<endl;
		return;
	}
	if(trail2 != NULL)
	{
		trail2->next = current2->next;
	}
	else
	{
		G.Vlist[v].firstNode = current2->next;
	}
	delete current2;
	G.Anumber--;//图内边个数-1
}

template<class T>
void graph<T>::dfs(int n)
{//深度优先搜索算法
	cout << G.Vlist[n].element;//输出起点顶点的元素（即数值）
	vertex[n] = false;//起点顶点在顶点记录数组中置为false，标记
	EdgeNode*p = G.Vlist[n].firstNode;//p是起点顶点的firstNode
	while(p)
	{//有相邻的顶点
		if(vertex[p->vertexAround])//为true，证明还没有被标记过
		{
			cout<<" ";//后边还有要输出的元素，输出空格
			dfs(p->vertexAround);//递归调用，标记经过的顶点
		}
		p=p->next;//起点顶点的相邻顶点都被标记完了，去其中一个相邻顶点
	}
}

template<class T>
void graph<T>::bfs(int n)
{//广度优先遍历
	linkedQueue<int>q;//队列q
	q.push(n);//将起点顶点push进队列q
	while(!q.empty())
	{
        //输出队列首的顶点
		cout<<G.Vlist[q.front()].element<<" ";
		//该顶点被标记
        vertex[q.front()] = false;
        //p是该顶点（刚被标记的节点）的firstNode
		EdgeNode*p = G.Vlist[q.front()].firstNode;
		while(p)
		{//该顶点有指向的顶点
			if(vertex[p->vertexAround])
			{
                //将该顶点的邻接顶点都标记了
				vertex[p->vertexAround] = false;
                //把这些邻接顶点都送入队列
				q.push(p->vertexAround);
			}
			p = p->next;//走向该顶点的下一个邻接顶点
		}
		q.pop();//把这个顶点从队列中pop掉
	}
	cout<<endl;
}

template<class T>
void graph<T>::dfsCounter(int n)
{//记录序列长度
	vertex[n] = false;//将节点n标记为false
	EdgeNode*p = G.Vlist[n].firstNode;//p是节点n的firstNode
	f++;//标记了一个，序列长度+1
	while(p)//节点n有指向的顶点（节点）
	{
		if(vertex[p->vertexAround])
		{
			dfsCounter(p->vertexAround);//递归标记
		}
		p = p->next;//向n节点指向的节点走
	}
}

template<class T>
void graph<T>::fdfs(int n)
{
	vertex[n] = false;//标记该点为false
	EdgeNode*p = G.Vlist[n].firstNode;//p是该点的firstNode
	while(p)
	{//n节点有指向的顶点
		if(vertex[p->vertexAround])
		{
			fdfs(p->vertexAround);//递归标记
		}
		p = p->next;//向n节点指向的节点走
	}
}

template<class T>
void graph<T>::components(int n)
{//记录图中的连通分量（即独立的子图个数） 
	int b = sizeof(vertex);
	for(int i = 0;i < b;i++)
	{//把顶点内数组的所有顶点初始化为true（未被标记）
		vertex[i] = true;
	}
	
	int flag = 0;//用于记录连通分量
	
	for(int i = 0;i < n;i++)//遍历所有顶点
	{
		if(vertex[i] == true)
		{
			fdfs(i);//标记这个顶点所能到的所有顶点
			flag++;//连通分量+1
		}
	}
	cout << flag << endl;//输出图中的连通分量
	
	//全部置为true以便不耽误其他功能使用
	for(int i = 0;i < b;i++)
	{
		vertex[i] = true;
	}
}

template<class T>
void graph<T>::everyComponents(int n)
{//所有连通分量中的最小点的编号，找到每个子图的最小顶点并输出
	int b = sizeof(vertex);
	for(int i = 0;i < b;i++)
	{//全部置为true
		vertex[i] = true;
	}
	
	for(int i = 0;i < n;i++)
	{
		if(vertex[i] == true)
		{
			cout << i+1 <<" ";//先输出该最小顶点的值
			fdfs(i);//标记该子图
		}
	}

	for(int i = 0;i < b;i++)
	{
		vertex[i] = true;
	}
	
	cout << endl;
}

template<class T>
void graph<T>::path(int x,int y)
{//输出从x到y的最短路径，用了bfs算法
	linkedQueue<int>q;
	int num = G.Vnumber + 1;//num是图G的边数+1，相当于从1开始
	q.push(x);//把起点顶点push进入队列
	vertex[q.front()] = false;
	int path[num];//长度为图G的边数的数组path用于记录路径
	for(int i = 0;i < num;i++)
	{
		path[i] = 0;//初始化path数组为0
	}
	while(!q.empty())//起点顶点有邻接顶点
	{
        //w是起点顶点
		int w = q.front();
        //将该点pop掉
		q.pop();
        //p是起点顶点的firstNode
		EdgeNode*p = G.Vlist[w].firstNode;
		while(p != NULL)//起点顶点有指向的元素
		{
			if(vertex[p->vertexAround])
			{
				if(p->vertexAround == y)
				{//起点顶点的链表中紧邻的邻接顶点就是终点y
					//输出最短路径
                    cout << path[w]+1 << endl;
					return;
				}
                //用于每次到新路径的时候+1
				path[p->vertexAround] = path[w]+1;
                //把起点顶点的邻接顶点放入队列
				q.push(p->vertexAround);
                //标记起点顶点的邻接顶点
				vertex[p->vertexAround] = false;
			}
			p = p->next;//到起点顶点的下一个邻接顶点
		}
	}
    //起点顶点没有能到达的邻接顶点，找不到最短路径，输出-1
	cout<<"-1"<<endl;
}
//----------------图论基础finish----------------

int main()
{
	//n代表图中点的个数，m代表接下来共有 m个操作，s代表起始点，t代表终点。
	int n,s,t,m;
	cin >> n >> m >> s >>  t;
	
	//定义图实例 
	graph<int> a(n);
	
	//m行操作输入 
	for(int i = 0;i < m;i++)
	{
		int operate;
		cin >> operate;
		if(operate == 0)
		{//点 u 和 v 之间增加一条边
			int u,v;
			cin >> u >> v;
			a.insert(u,v);
		}
		else if(operate==1)
		{//删除点 u 和 v 之间的边
			int u,v;
			cin >> u >> v;
			a.erase(u,v);
		}
	}
	
	//第一行输出图中有多少个连通分量
	a.components(n);
	//第二行输出所有连通子图中最小点的编号
	a.everyComponents(n);
	//第三行输出从 s 点开始的 dfs 序列长度
	a.dfsCounter(s-1);
	cout << f << endl;
	f = 0;
	int b = sizeof(vertex);
	for(int i = 0;i < b;i++)
	{
		vertex[i] = true;
	}
	//第四行输出从 s 点开始的字典序最小的 dfs 序列
	a.dfs(s-1);
	cout << endl;
	for(int i = 0;i < b;i++)
	{
		vertex[i] = true;
	}
	//第五行输出从 t 点开始的 bfs 序列的长度 
	a.dfsCounter(t-1);//输出从t点开始的bfs序列长度
	cout << f << endl;
	f = 0;
	for(int i = 0;i < b;i++)
	{
		vertex[i] = true;
	}
	//第六行输出从 t 点开始字典序最小的 bfs 序列
	a.bfs(t-1);
	for(int i = 0;i < b;i++)
	{
		vertex[i] = true;
	}
	//第七行输出从 s 点到 t 点的最短路径，若是不存在路径则输出-1
	a.path(s-1,t-1);
	return 0;
}