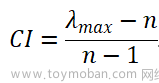目录
目录
1 算法讲解
1.1解决评价类问题的一般步骤：
1.2 如何确定权重
1.2.1 判断矩阵的bug
1.2.2 一致性检验
1.2.3 计算权重
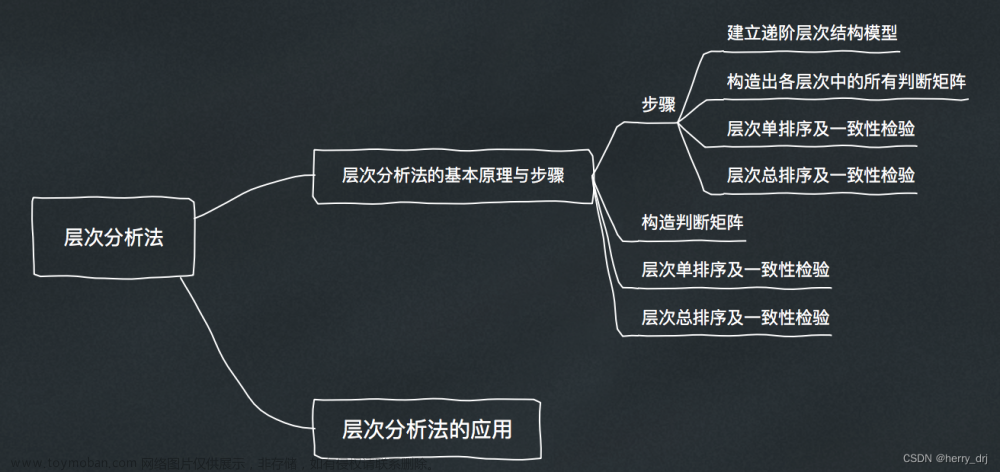
1.3 层次分析法具体步骤
1.3.1 建立层次结构
1.3.2 构造判断矩阵
1.3.3 一致性检验，计算权重
1.4 层次分析法局限性
2 代码
3 模型拓展
3.1 多个准则层
用来解决评价类问题
1 算法讲解
⭐层次分析法是用来解决评价类问题的
1.1解决评价类问题的一般步骤：
1. 评价的目标是什么？
例如，最佳的旅游景点
2. 有哪几种方案可选？
例如，去苏杭、北戴河、桂林
3. 评价的标准为什么
题目中一般不会直接告知，可以通过查找资料获取评价标准
i.虫部落很厉害 虫部落 - 让搜索更简单
ii.根据关键字查论文，例如旅游选择因素，旅游经典评价指标。引用论文显得专业。
without lose of generality，指标为景色，花费，居住，饮食，交通。
1.2 如何确定权重
好，那么接下来我们只需要知道这五个指标的比重就可以了
也就是说，只要先填好这个表的蓝色区域就可以了。但是一次考虑五个因素，容易考虑不周（因为五个因素的权重加起来应该是1）。所以我们先两个两个对比，然后再退出来所有的就好。
即为上图所示，例如，景色和居住比起来，景色稍微重要一些，那么对应格子就填4。
这实际上是一个正互反矩阵（也是层次分析法中的判断矩阵）：
- aij的意义是，与j相比，i的重要性
- i=j时，aij=1，即对角线元素为1
- aij与aji乘积为1，且aij＞0
那么，计算出不同因素之间的权重后，不同景点在同一因素下的得分如何计算捏？
同理：以景色为例，我们再整一个判断矩阵
同理：
1.2.1 判断矩阵的bug
那么矩阵会不会出bug捏？
啊当然是有可能滴！
就是出现了一个A大于B，B大于A的情况
上述出现的是一种不一致的现象，既然有不一致，那么就有与之对应的一致，不然说一个矩阵不一致，就毫无意义，那么什么是一致？
若完全一致：
例如：
这就是一个完全一致的矩阵，显然，矩阵的各行/各列之间成倍数关系
那么由此我们就可以得到一致矩阵的定义哩，若一个正互反矩阵是满足ajk=aji*aik（或者各行各列成倍数关系），就叫它一致矩阵。
于是，在进行判断矩阵求权重前，一定要先检验一致性
当然完全的一致性是不现实的，哪能那么准，如果真这么准那咱哪还用什么两两比较，直接五个一块比不就行了，所以只要不一致在一个范围内不要太离谱就行。
1.2.2 一致性检验
I.检验原理：
引理：
II.检验步骤：
1.2.3 计算权重
（归一化：让结果只和等于1）
一致矩阵各行各列都是成比例的，所以只要拿单独一列算就可以了
不一致矩阵：
I. 方法一：算数平均法求权重
（注意权重经过归一化了，加起来一定是1，不为1可能是因为四舍五入的影响）
数学表述：
II. 方法二：几何平均法求权重
III. 方法三：特征值法（使用的最多）
为什么刚好是一致矩阵的第一列？
看这个
一致性矩阵对角线元素都是1，那么我们看第二行，第一行的二分之一想变成第二行的1，就得用二分之一除以二分之一，那么各行成比例，所以第一列的第二个元素2就是1除以二分之一得到的，同理，第一列第三个元素就是一除以四得到的。
1.3 层次分析法具体步骤
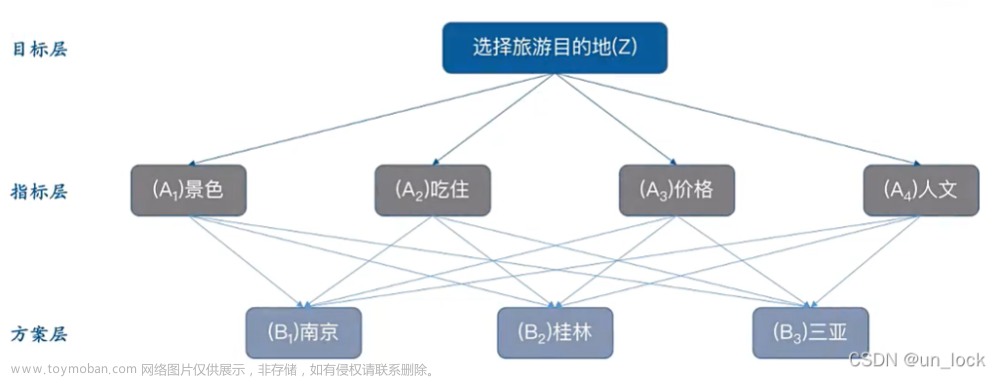
1.3.1 建立层次结构
（图可以用process on做）
1.3.2 构造判断矩阵
判断矩阵说是专家经过商议后得出的，但是实际上都是自己填的，写完判断矩阵之后不用说是专家商议得出的还是自己填的，略过这个话题就可以。
例如：
直接把矩阵摆出来就可以了，不提来源这个事。
但是填矩阵的时候尽可能搜一些资料，有一定的依据。
1.3.3 一致性检验，计算权重
如果检验出来一致性太弱了，那就按照倍数关系调整调整就行了
1.3.4 算得分
可以用excel算起来方便点
1.4 层次分析法局限性
因为层次分析法的判断矩阵是自己填出来的，那数据已知再自己填就不得行了。
2 代码
（待完善）
3 模型拓展
3.1 多个准则层
按照判断矩阵一层一层往下套就行啦
3.2 不一一对应
文章来源：https://www.toymoban.com/news/detail-765675.html
准则层不关联所有的方案层，直接把没有连的那层的权重设为0就可以了。文章来源地址https://www.toymoban.com/news/detail-765675.html
到了这里，关于层次分析法(AHP）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
